Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 tập 1 của giaitoan.edu.vn. Chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho tất cả các bài tập trong sách giáo khoa Toán 12 Kết nối tri thức.
Ở bài viết này, chúng ta sẽ cùng nhau giải quyết các bài tập trong mục 2 trang 9, 10, 11. Mục tiêu là giúp các em nắm vững kiến thức và kỹ năng giải toán, tự tin hơn trong các kỳ thi.
Cực trị của hàm số
Trả lời câu hỏi Vận dụng 2 trang 12 SGK Toán 12 Kết nối tri thức
Một vật được phóng thẳng đứng lên trên từ độ cao 2m với vận tốc ban đầu là 24,5m/s. Trong Vật lí, ta biết rằng khi bỏ qua sức cản của không khí thì độ cao h (mét) của vật sau t (giây) được cho bởi công thức: \(h\left( t \right) = 2 + 24,5t - 4,9{t^2}\). Hỏi tại thời điểm nào thì vật đạt độ cao lớn nhất?
Phương pháp giải:
Sử dụng kiến thức về cách tìm cực trị của hàm số \(y = f\left( x \right)\) để tìm thời điểm vật đạt độ cao lớn nhất:
1. Tìm tập xác định của hàm số.
2. Tính đạo hàm f’(x). Tìm các điểm mà tại đó đạo hàm f’(x) bằng 0 hoặc đạo hàm không tồn tại.
3. Lập bảng biến thiên của hàm số.
4. Từ bảng biến thiên suy ra các cực trị của hàm số.
Lời giải chi tiết:
Xét hàm số: \(h\left( t \right) = 2 + 24,5t - 4,9{t^2}\).
Tập xác định của hàm số là \(\mathbb{R}\).
Ta có: \[h'\left( t \right) = - 9,8t + 24,5;h'\left( t \right) = 0 \Leftrightarrow - 9,8t + 24,5 = 0 \Leftrightarrow t = \frac{5}{2}\].
Bảng biến thiên:
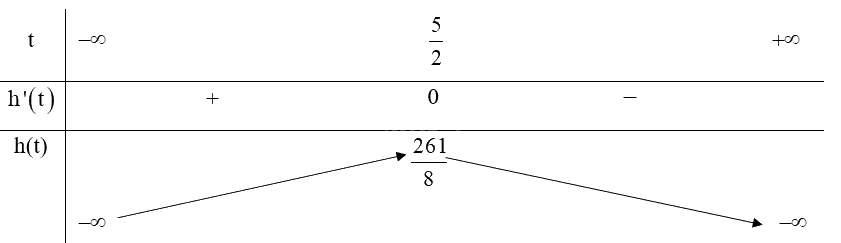
Từ bảng biến thiên ta có:
Hàm số đạt cực đại tại \(t = \frac{5}{2}\),
Vậy thời điểm vật đạt độ cao lớn nhất là \(t = \frac{5}{2}\) giây
Trả lời câu hỏi Hoạt động 5 trang 10 SGK Toán 12 Kết nối tri thức
Cho hàm số \(y = \frac{1}{3}{x^3} - 3{x^2} + 8x + 1\).
a) Tính đạo hàm \(f'\left( x \right)\) và tìm các điểm mà tại đó đạo hàm \(f'\left( x \right)\) bằng 0.
b) Lập bảng biến thiên của hàm số.
c) Từ bảng biến thiên suy ra các điểm cực trị của hàm số.
Phương pháp giải:
Sử dụng kiến thức về định nghĩa cực đại, cực tiểu của hàm số để tìm cực đại, cực tiểu của hàm số: Cho hàm số \(y = f\left( x \right)\) xác định và liên tục trên khoảng (a; b) (a có thể là \( - \infty \), b có thể là \( + \infty \)) và điểm \({x_0} \in \left( {a;b} \right)\).
+ Nếu tồn tại số \(h > 0\) sao cho \(f\left( x \right) < f\left( {{x_0}} \right)\) với mọi \(x \in \left( {{x_0} - h;{x_0} + h} \right) \subset \left( {a;b} \right)\) và \(x \ne {x_0}\) thì ta nói hàm số f(x) đạt cực đại tại \({x_0}\).
+ Nếu tồn tại số \(h > 0\) sao cho \(f\left( x \right) > f\left( {{x_0}} \right)\) với mọi \(x \in \left( {{x_0} - h;{x_0} + h} \right) \subset \left( {a;b} \right)\) và \(x \ne {x_0}\) thì ta nói hàm số f(x) đạt cực tiểu tại \({x_0}\).
Lời giải chi tiết:
a) Tập xác định: \(D = \mathbb{R}\).
\(y' = {x^2} - 6x + 8\), \(y' = 0 \Leftrightarrow {x^2} - 6x + 8 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 4\\x = 2\end{array} \right.\)
Vậy \(x = 4;x = 2\) thì \(f'\left( x \right) = 0\)
b) Bảng biến thiên:
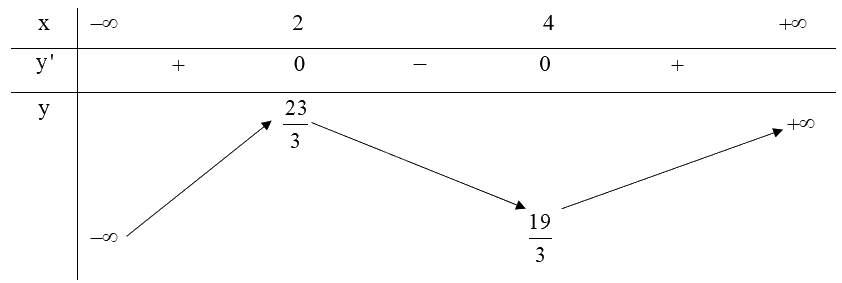
c) Từ bảng biến thiên ta có:
Hàm số \(y = \frac{1}{3}{x^3} - 3{x^2} + 8x + 1\) có điểm cực đại là \(\left( {2;\frac{{23}}{3}} \right)\).
Hàm số \(y = \frac{1}{3}{x^3} - 3{x^2} + 8x + 1\) có điểm cực tiểu là \(\left( {4;\frac{{19}}{3}} \right)\).
Trả lời câu hỏi Luyện tập 5 trang 12 SGK Toán 12 Kết nối tri thức
Tìm cực trị của các hàm số sau:
a) \(y = {x^4} - 3{x^2} + 1\);
b) \(y = \frac{{ - {x^2} + 2x - 1}}{{x + 2}}\).
Phương pháp giải:
Sử dụng kiến thức về cách tìm cực trị của hàm số \(y = f\left( x \right)\) để tìm cực trị của hàm số:
1. Tìm tập xác định của hàm số.
2. Tính đạo hàm f’(x). Tìm các điểm mà tại đó đạo hàm f’(x) bằng 0 hoặc đạo hàm không tồn tại.
3. Lập bảng biến thiên của hàm số.
4. Từ bảng biến thiên suy ra các cực trị của hàm số.
Lời giải chi tiết:
a) Tập xác định của hàm số là \(\mathbb{R}\).
Ta có: \(y' = 4{x^3} - 6x,y' = 0 \Leftrightarrow 4{x^3} - 6x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \pm \frac{{\sqrt 6 }}{2}\end{array} \right.\);
Bảng biến thiên:
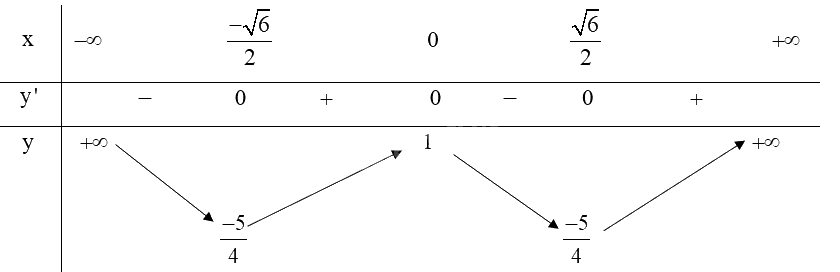
Từ bảng biến thiên ta có:
Hàm số đạt cực đại tại \(x = 0\) và .
Hàm số đạt cực tiểu tại \(x = \pm \frac{{\sqrt 6 }}{2}\) và \({y_{CT}} = \frac{{ - 5}}{4}\).
b) Tập xác định: \(D = \mathbb{R}\backslash \left\{ { - 2} \right\}\).
Ta có: \(y' = \frac{{\left( { - 2x + 2} \right)\left( {x + 2} \right) - \left( { - {x^2} + 2x - 1} \right)}}{{{{\left( {x + 2} \right)}^2}}} = \frac{{ - {x^2} - 4x + 5}}{{{{\left( {x + 2} \right)}^2}}}\)
\(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 5\\x = 1\end{array} \right.\) (thỏa mãn)
Lập bảng biến thiên của hàm số:
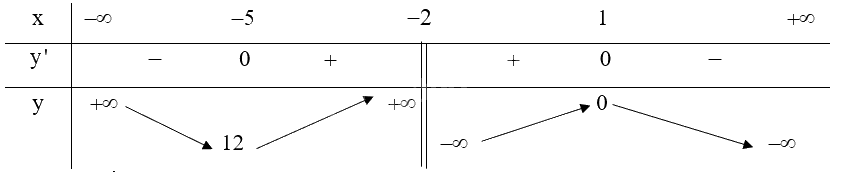
Từ bảng biến thiên ta có:
Hàm số đạt cực đại tại \(x = 1\) và .
Hàm số đạt cực tiểu tại \(x = - 5\) và \({y_{CT}} = 12\).
Trả lời câu hỏi trang 11 SGK Toán 12 Kết nối tri thức
Giải thích vì sao nếu f’(x) không đổi dấu qua \({x_0}\) thì \({x_0}\) không phải là điểm cực trị của hàm số f(x)?
Phương pháp giải:
Sử dụng kiến thức về định lí cực trị hàm số để chứng minh: Giả sử hàm số \(y = f\left( x \right)\) liên tục trên khoảng (a; b) chứa điểm \({x_0}\) và có đạo hàm trên các khoảng \(\left( {a;{x_0}} \right)\) và \(\left( {{x_0};b} \right)\). Khi đó:
+ Nếu \(f'\left( x \right) < 0\) với mọi \(x \in \left( {a;{x_0}} \right)\) và \(f'\left( x \right) > 0\) với mọi \(x \in \left( {{x_0};b} \right)\) thì điểm \({x_0}\) là một điểm cực tiểu của hàm số f(x).
+ Nếu \(f'\left( x \right) > 0\) với mọi \(x \in \left( {a;{x_0}} \right)\) và \(f'\left( x \right) < 0\) với mọi \(x \in \left( {{x_0};b} \right)\) thì điểm \({x_0}\) là một điểm cực đại của hàm số f(x).d
Lời giải chi tiết:
Giả sử hàm số \(y = f\left( x \right)\) liên tục trên khoảng (a; b) chứa điểm \({x_0}\) và có đạo hàm trên các khoảng \(\left( {a;{x_0}} \right)\) và \(\left( {{x_0};b} \right)\). Nếu f’(x) không đổi dấu qua \({x_0}\) thì:
TH1: \(f'\left( x \right) < 0\) với mọi \(x \in \left( {a;{x_0}} \right)\) và \(f'\left( x \right) < 0\) với mọi \(x \in \left( {{x_0};b} \right)\), ta có bảng biến thiên:
Giả sử hàm số \(y = f\left( x \right)\) liên tục trên khoảng (a; b) chứa điểm \({x_0}\) và có đạo hàm trên các khoảng \(\left( {a;{x_0}} \right)\) và \(\left( {{x_0};b} \right)\). Nếu f’(x) không đổi dấu qua \({x_0}\) thì:
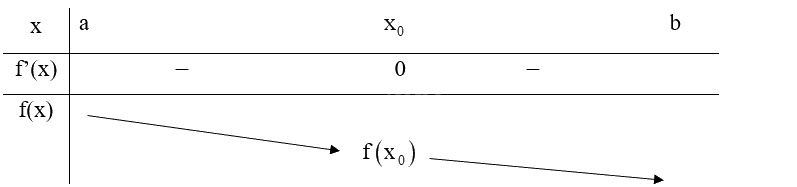
TH1: \(f'\left( x \right) < 0\) với mọi \(x \in \left( {a;{x_0}} \right)\) và \(f'\left( x \right) < 0\) với mọi \(x \in \left( {{x_0};b} \right)\), ta có bảng biến thiên:
Do đó, \({x_0}\) không phải là điểm cực trị của hàm số f(x).
Trả lời câu hỏi Luyện tập 4 trang 10 SGK Toán 12 Kết nối tri thức
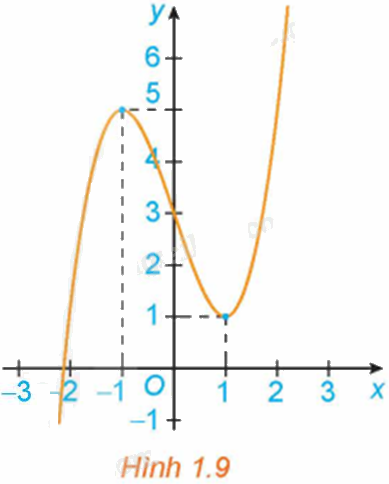
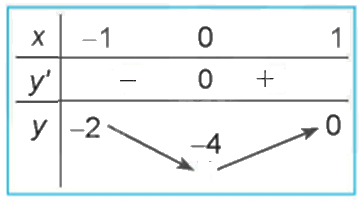
Hình 1.9 là đồ thị của hàm số \(y = f\left( x \right)\). Hãy tìm các cực trị của hàm số.
Phương pháp giải:
Sử dụng kiến thức về định nghĩa cực đại, cực tiểu của hàm số để tìm cực đại, cực tiểu của hàm số: Cho hàm số \(y = f\left( x \right)\) xác định và liên tục trên khoảng (a; b) (a có thể là \( - \infty \), b có thể là \( + \infty \)) và điểm \({x_0} \in \left( {a;b} \right)\).
+ Nếu tồn tại số \(h > 0\) sao cho \(f\left( x \right) < f\left( {{x_0}} \right)\) với mọi \(x \in \left( {{x_0} - h;{x_0} + h} \right) \subset \left( {a;b} \right)\) và \(x \ne {x_0}\) thì ta nói hàm số f(x) đạt cực đại tại \({x_0}\).
+ Nếu tồn tại số \(h > 0\) sao cho \(f\left( x \right) > f\left( {{x_0}} \right)\) với mọi \(x \in \left( {{x_0} - h;{x_0} + h} \right) \subset \left( {a;b} \right)\) và \(x \ne {x_0}\) thì ta nói hàm số f(x) đạt cực tiểu tại \({x_0}\).
Lời giải chi tiết:
Từ đồ thị hàm số, ta có:
Hàm số đạt cực tiểu tại \(x = 1\) và \({y_{CT}} = y\left( 1 \right) = 1\).
Hàm số đạt cực đại tại \(x = - 1\) và \({y_{C{\rm{D}}}} = y( - 1) = 5\)
Trả lời câu hỏi Hoạt động 4 trang 9 SGK Toán 12 Kết nối tri thức
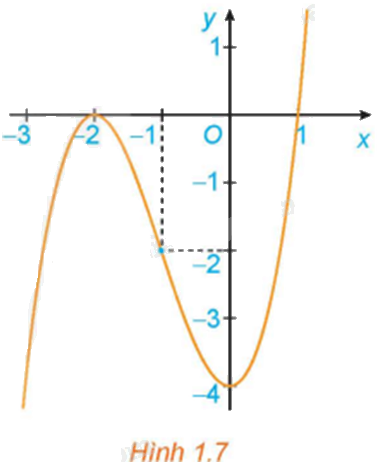
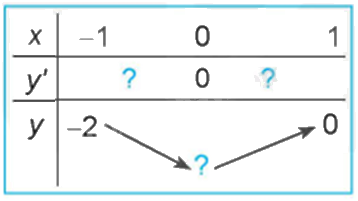
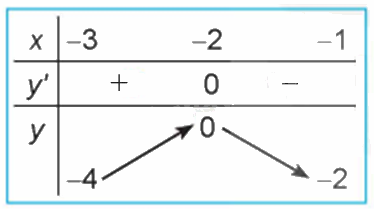
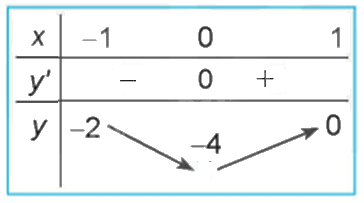
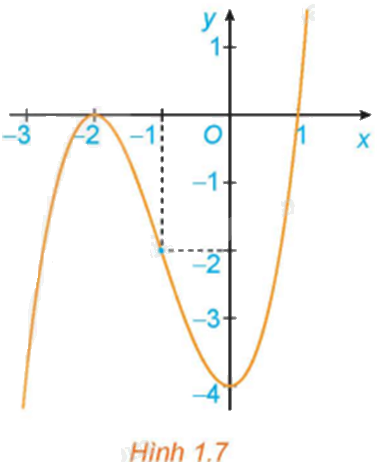
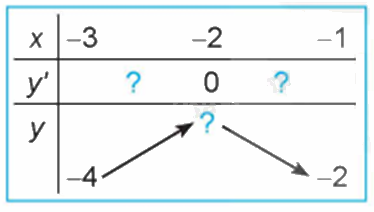
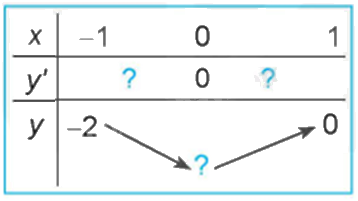
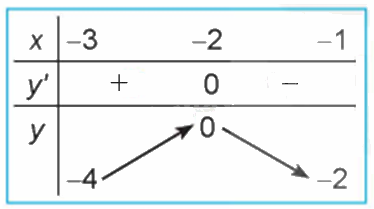
Quan sát đồ thị của hàm số \(y = {x^3} + 3{x^2} - 4\) (H.1.7). Xét dấu đạo hàm của hàm số đã cho và hoàn thành các bảng sau vào vở:
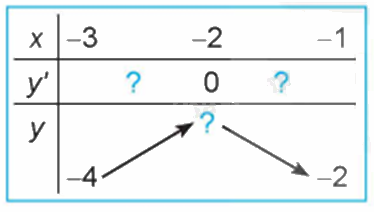
Phương pháp giải:
- Sử dụng kiến thức về định lí về tính đồng biến, nghịch biến của hàm số để tìm khoảng đồng biến, nghịch biến: Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên khoảng K.
+ Nếu \(f'\left( x \right) > 0\) với mọi \(x \in K\) thì hàm số \(f\left( x \right)\) đồng biến trên khoảng K.
+ Nếu \(f'\left( x \right) < 0\) với mọi \(x \in K\) thì hàm số \(f\left( x \right)\) nghịch biến trên khoảng K.
Lời giải chi tiết:
Trả lời câu hỏi Hoạt động 4 trang 9 SGK Toán 12 Kết nối tri thức
Quan sát đồ thị của hàm số \(y = {x^3} + 3{x^2} - 4\) (H.1.7). Xét dấu đạo hàm của hàm số đã cho và hoàn thành các bảng sau vào vở:
Phương pháp giải:
- Sử dụng kiến thức về định lí về tính đồng biến, nghịch biến của hàm số để tìm khoảng đồng biến, nghịch biến: Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên khoảng K.
+ Nếu \(f'\left( x \right) > 0\) với mọi \(x \in K\) thì hàm số \(f\left( x \right)\) đồng biến trên khoảng K.
+ Nếu \(f'\left( x \right) < 0\) với mọi \(x \in K\) thì hàm số \(f\left( x \right)\) nghịch biến trên khoảng K.
Lời giải chi tiết:
Trả lời câu hỏi Luyện tập 4 trang 10 SGK Toán 12 Kết nối tri thức
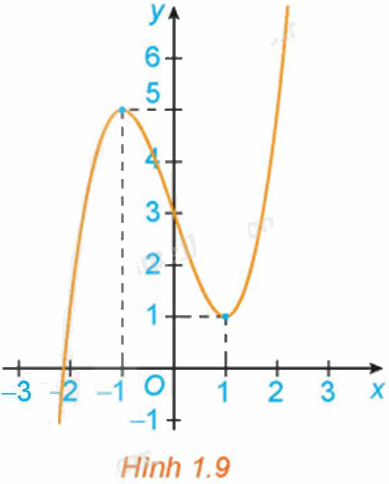
Hình 1.9 là đồ thị của hàm số \(y = f\left( x \right)\). Hãy tìm các cực trị của hàm số.
Phương pháp giải:
Sử dụng kiến thức về định nghĩa cực đại, cực tiểu của hàm số để tìm cực đại, cực tiểu của hàm số: Cho hàm số \(y = f\left( x \right)\) xác định và liên tục trên khoảng (a; b) (a có thể là \( - \infty \), b có thể là \( + \infty \)) và điểm \({x_0} \in \left( {a;b} \right)\).
+ Nếu tồn tại số \(h > 0\) sao cho \(f\left( x \right) < f\left( {{x_0}} \right)\) với mọi \(x \in \left( {{x_0} - h;{x_0} + h} \right) \subset \left( {a;b} \right)\) và \(x \ne {x_0}\) thì ta nói hàm số f(x) đạt cực đại tại \({x_0}\).
+ Nếu tồn tại số \(h > 0\) sao cho \(f\left( x \right) > f\left( {{x_0}} \right)\) với mọi \(x \in \left( {{x_0} - h;{x_0} + h} \right) \subset \left( {a;b} \right)\) và \(x \ne {x_0}\) thì ta nói hàm số f(x) đạt cực tiểu tại \({x_0}\).
Lời giải chi tiết:
Từ đồ thị hàm số, ta có:
Hàm số đạt cực tiểu tại \(x = 1\) và \({y_{CT}} = y\left( 1 \right) = 1\).
Hàm số đạt cực đại tại \(x = - 1\) và \({y_{C{\rm{D}}}} = y( - 1) = 5\)
Trả lời câu hỏi Hoạt động 5 trang 10 SGK Toán 12 Kết nối tri thức
Cho hàm số \(y = \frac{1}{3}{x^3} - 3{x^2} + 8x + 1\).
a) Tính đạo hàm \(f'\left( x \right)\) và tìm các điểm mà tại đó đạo hàm \(f'\left( x \right)\) bằng 0.
b) Lập bảng biến thiên của hàm số.
c) Từ bảng biến thiên suy ra các điểm cực trị của hàm số.
Phương pháp giải:
Sử dụng kiến thức về định nghĩa cực đại, cực tiểu của hàm số để tìm cực đại, cực tiểu của hàm số: Cho hàm số \(y = f\left( x \right)\) xác định và liên tục trên khoảng (a; b) (a có thể là \( - \infty \), b có thể là \( + \infty \)) và điểm \({x_0} \in \left( {a;b} \right)\).
+ Nếu tồn tại số \(h > 0\) sao cho \(f\left( x \right) < f\left( {{x_0}} \right)\) với mọi \(x \in \left( {{x_0} - h;{x_0} + h} \right) \subset \left( {a;b} \right)\) và \(x \ne {x_0}\) thì ta nói hàm số f(x) đạt cực đại tại \({x_0}\).
+ Nếu tồn tại số \(h > 0\) sao cho \(f\left( x \right) > f\left( {{x_0}} \right)\) với mọi \(x \in \left( {{x_0} - h;{x_0} + h} \right) \subset \left( {a;b} \right)\) và \(x \ne {x_0}\) thì ta nói hàm số f(x) đạt cực tiểu tại \({x_0}\).
Lời giải chi tiết:
a) Tập xác định: \(D = \mathbb{R}\).
\(y' = {x^2} - 6x + 8\), \(y' = 0 \Leftrightarrow {x^2} - 6x + 8 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 4\\x = 2\end{array} \right.\)
Vậy \(x = 4;x = 2\) thì \(f'\left( x \right) = 0\)
b) Bảng biến thiên:
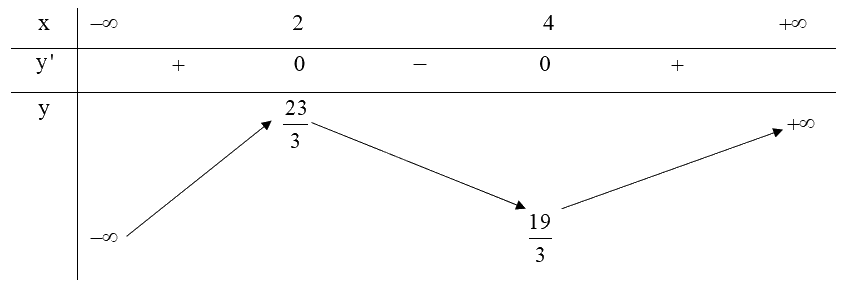
c) Từ bảng biến thiên ta có:
Hàm số \(y = \frac{1}{3}{x^3} - 3{x^2} + 8x + 1\) có điểm cực đại là \(\left( {2;\frac{{23}}{3}} \right)\).
Hàm số \(y = \frac{1}{3}{x^3} - 3{x^2} + 8x + 1\) có điểm cực tiểu là \(\left( {4;\frac{{19}}{3}} \right)\).
Trả lời câu hỏi trang 11 SGK Toán 12 Kết nối tri thức
Giải thích vì sao nếu f’(x) không đổi dấu qua \({x_0}\) thì \({x_0}\) không phải là điểm cực trị của hàm số f(x)?
Phương pháp giải:
Sử dụng kiến thức về định lí cực trị hàm số để chứng minh: Giả sử hàm số \(y = f\left( x \right)\) liên tục trên khoảng (a; b) chứa điểm \({x_0}\) và có đạo hàm trên các khoảng \(\left( {a;{x_0}} \right)\) và \(\left( {{x_0};b} \right)\). Khi đó:
+ Nếu \(f'\left( x \right) < 0\) với mọi \(x \in \left( {a;{x_0}} \right)\) và \(f'\left( x \right) > 0\) với mọi \(x \in \left( {{x_0};b} \right)\) thì điểm \({x_0}\) là một điểm cực tiểu của hàm số f(x).
+ Nếu \(f'\left( x \right) > 0\) với mọi \(x \in \left( {a;{x_0}} \right)\) và \(f'\left( x \right) < 0\) với mọi \(x \in \left( {{x_0};b} \right)\) thì điểm \({x_0}\) là một điểm cực đại của hàm số f(x).d
Lời giải chi tiết:
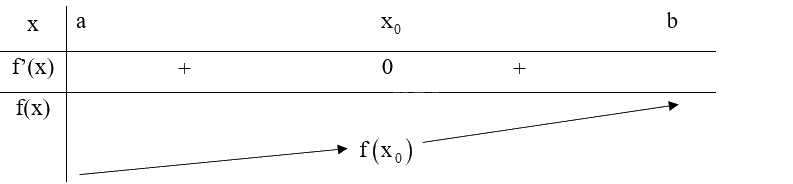
Giả sử hàm số \(y = f\left( x \right)\) liên tục trên khoảng (a; b) chứa điểm \({x_0}\) và có đạo hàm trên các khoảng \(\left( {a;{x_0}} \right)\) và \(\left( {{x_0};b} \right)\). Nếu f’(x) không đổi dấu qua \({x_0}\) thì:
TH1: \(f'\left( x \right) < 0\) với mọi \(x \in \left( {a;{x_0}} \right)\) và \(f'\left( x \right) < 0\) với mọi \(x \in \left( {{x_0};b} \right)\), ta có bảng biến thiên:
Giả sử hàm số \(y = f\left( x \right)\) liên tục trên khoảng (a; b) chứa điểm \({x_0}\) và có đạo hàm trên các khoảng \(\left( {a;{x_0}} \right)\) và \(\left( {{x_0};b} \right)\). Nếu f’(x) không đổi dấu qua \({x_0}\) thì:
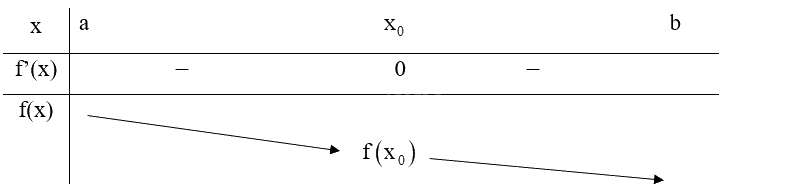
TH1: \(f'\left( x \right) < 0\) với mọi \(x \in \left( {a;{x_0}} \right)\) và \(f'\left( x \right) < 0\) với mọi \(x \in \left( {{x_0};b} \right)\), ta có bảng biến thiên:
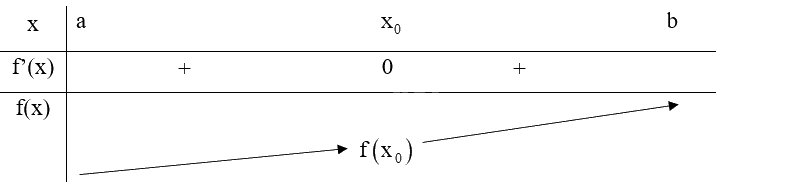
Do đó, \({x_0}\) không phải là điểm cực trị của hàm số f(x).
Trả lời câu hỏi Luyện tập 5 trang 12 SGK Toán 12 Kết nối tri thức
Tìm cực trị của các hàm số sau:
a) \(y = {x^4} - 3{x^2} + 1\);
b) \(y = \frac{{ - {x^2} + 2x - 1}}{{x + 2}}\).
Phương pháp giải:
Sử dụng kiến thức về cách tìm cực trị của hàm số \(y = f\left( x \right)\) để tìm cực trị của hàm số:
1. Tìm tập xác định của hàm số.
2. Tính đạo hàm f’(x). Tìm các điểm mà tại đó đạo hàm f’(x) bằng 0 hoặc đạo hàm không tồn tại.
3. Lập bảng biến thiên của hàm số.
4. Từ bảng biến thiên suy ra các cực trị của hàm số.
Lời giải chi tiết:
a) Tập xác định của hàm số là \(\mathbb{R}\).
Ta có: \(y' = 4{x^3} - 6x,y' = 0 \Leftrightarrow 4{x^3} - 6x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \pm \frac{{\sqrt 6 }}{2}\end{array} \right.\);
Bảng biến thiên:
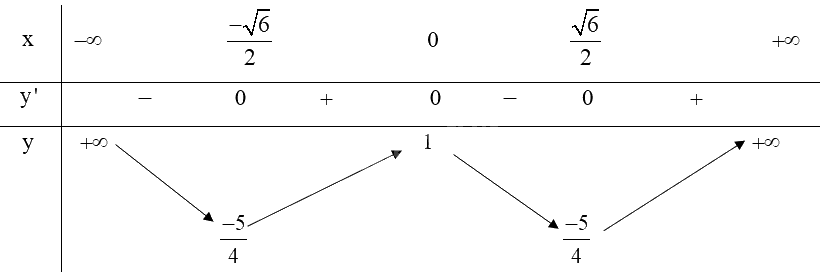
Từ bảng biến thiên ta có:
Hàm số đạt cực đại tại \(x = 0\) và .
Hàm số đạt cực tiểu tại \(x = \pm \frac{{\sqrt 6 }}{2}\) và \({y_{CT}} = \frac{{ - 5}}{4}\).
b) Tập xác định: \(D = \mathbb{R}\backslash \left\{ { - 2} \right\}\).
Ta có: \(y' = \frac{{\left( { - 2x + 2} \right)\left( {x + 2} \right) - \left( { - {x^2} + 2x - 1} \right)}}{{{{\left( {x + 2} \right)}^2}}} = \frac{{ - {x^2} - 4x + 5}}{{{{\left( {x + 2} \right)}^2}}}\)
\(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 5\\x = 1\end{array} \right.\) (thỏa mãn)
Lập bảng biến thiên của hàm số:
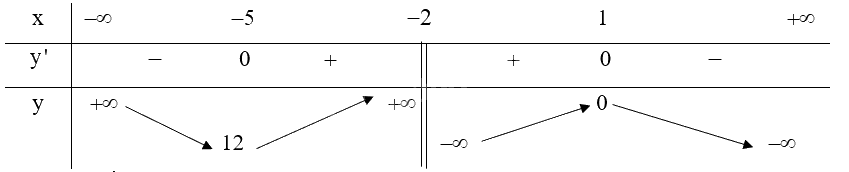
Từ bảng biến thiên ta có:
Hàm số đạt cực đại tại \(x = 1\) và .
Hàm số đạt cực tiểu tại \(x = - 5\) và \({y_{CT}} = 12\).
Trả lời câu hỏi Vận dụng 2 trang 12 SGK Toán 12 Kết nối tri thức
Một vật được phóng thẳng đứng lên trên từ độ cao 2m với vận tốc ban đầu là 24,5m/s. Trong Vật lí, ta biết rằng khi bỏ qua sức cản của không khí thì độ cao h (mét) của vật sau t (giây) được cho bởi công thức: \(h\left( t \right) = 2 + 24,5t - 4,9{t^2}\). Hỏi tại thời điểm nào thì vật đạt độ cao lớn nhất?
Phương pháp giải:
Sử dụng kiến thức về cách tìm cực trị của hàm số \(y = f\left( x \right)\) để tìm thời điểm vật đạt độ cao lớn nhất:
1. Tìm tập xác định của hàm số.
2. Tính đạo hàm f’(x). Tìm các điểm mà tại đó đạo hàm f’(x) bằng 0 hoặc đạo hàm không tồn tại.
3. Lập bảng biến thiên của hàm số.
4. Từ bảng biến thiên suy ra các cực trị của hàm số.
Lời giải chi tiết:
Xét hàm số: \(h\left( t \right) = 2 + 24,5t - 4,9{t^2}\).
Tập xác định của hàm số là \(\mathbb{R}\).
Ta có: \[h'\left( t \right) = - 9,8t + 24,5;h'\left( t \right) = 0 \Leftrightarrow - 9,8t + 24,5 = 0 \Leftrightarrow t = \frac{5}{2}\].
Bảng biến thiên:
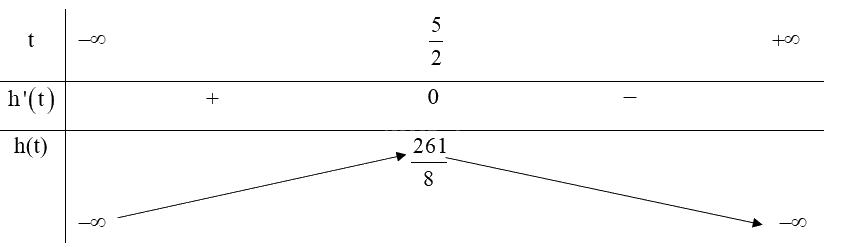
Từ bảng biến thiên ta có:
Hàm số đạt cực đại tại \(t = \frac{5}{2}\),
Vậy thời điểm vật đạt độ cao lớn nhất là \(t = \frac{5}{2}\) giây
Mục 2 của SGK Toán 12 tập 1 Kết nối tri thức tập trung vào việc nghiên cứu về giới hạn của hàm số. Đây là một khái niệm nền tảng quan trọng trong giải tích, đóng vai trò then chốt trong việc hiểu các khái niệm phức tạp hơn như đạo hàm và tích phân. Việc nắm vững kiến thức về giới hạn hàm số không chỉ giúp học sinh giải quyết các bài tập trong sách giáo khoa mà còn là bước đệm quan trọng cho việc học tập nâng cao.
Mục 2 bao gồm các nội dung chính sau:
Trang 9 SGK Toán 12 tập 1 Kết nối tri thức chứa các bài tập vận dụng kiến thức về khái niệm giới hạn để tính giới hạn của các hàm số đơn giản. Các bài tập này thường yêu cầu học sinh áp dụng định nghĩa giới hạn và các tính chất cơ bản để tìm ra kết quả.
Ví dụ, bài tập 1 yêu cầu tính giới hạn của hàm số f(x) = 2x + 1 khi x tiến tới 2. Lời giải như sau:
lim (x→2) (2x + 1) = 2 * 2 + 1 = 5
Trang 10 tập trung vào các bài tập phức tạp hơn, yêu cầu học sinh sử dụng các kỹ năng biến đổi đại số để đơn giản hóa biểu thức trước khi tính giới hạn. Một số bài tập còn yêu cầu học sinh sử dụng các định lý giới hạn để giải quyết.
Ví dụ, bài tập 3 yêu cầu tính giới hạn của hàm số f(x) = (x^2 - 1) / (x - 1) khi x tiến tới 1. Lời giải như sau:
lim (x→1) (x^2 - 1) / (x - 1) = lim (x→1) (x - 1)(x + 1) / (x - 1) = lim (x→1) (x + 1) = 1 + 1 = 2
Trang 11 giới thiệu các bài tập liên quan đến giới hạn tại vô cùng. Các bài tập này thường yêu cầu học sinh chia cả tử và mẫu cho lũy thừa cao nhất của x để đơn giản hóa biểu thức và tìm ra giới hạn.
Ví dụ, bài tập 5 yêu cầu tính giới hạn của hàm số f(x) = (2x^2 + 1) / (x^2 + 3) khi x tiến tới vô cùng. Lời giải như sau:
lim (x→∞) (2x^2 + 1) / (x^2 + 3) = lim (x→∞) (2 + 1/x^2) / (1 + 3/x^2) = 2 / 1 = 2
Hy vọng rằng với lời giải chi tiết và những lời khuyên trên, các em học sinh đã có thể tự tin giải quyết các bài tập trong mục 2 trang 9, 10, 11 SGK Toán 12 tập 1 Kết nối tri thức. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!