Bài tập 1.6 trang 14 SGK Toán 12 tập 1 thuộc chương trình học Toán 12 Kết nối tri thức, tập trung vào việc rèn luyện kỹ năng về giới hạn của hàm số. Bài tập này thường yêu cầu học sinh vận dụng các định nghĩa và tính chất của giới hạn để giải quyết các bài toán cụ thể.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập 1.6 trang 14 SGK Toán 12 tập 1, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
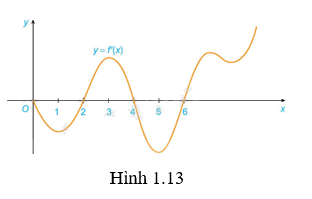
Đồ thị của đạo hàm bậc nhất (y = f'left( x right)) của hàm số f(x) được cho trong Hình 1.13: a) Hàm số f(x) đồng biến trên những khoảng nào? Giải thích. b) Tại giá trị nào của x thì f(x) có cực đại hoặc cực tiểu? Giải thích.
Đề bài
Đồ thị của đạo hàm bậc nhất \(y = f'\left( x \right)\) của hàm số f(x) được cho trong Hình 1.13:a) Hàm số f(x) đồng biến trên những khoảng nào? Giải thích.b) Tại giá trị nào của x thì f(x) có cực đại hoặc cực tiểu? Giải thích.
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về tính đồng biến, nghịch biến của hàm số để tìm khoảng đồng biến, nghịch biến: Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên khoảng K.
+ Nếu \(f'\left( x \right) > 0\) với mọi \(x \in K\) thì hàm số \(f\left( x \right)\) đồng biến trên khoảng K.
+ Nếu \(f'\left( x \right) < 0\) với mọi \(x \in K\) thì hàm số \(f\left( x \right)\) nghịch biến trên khoảng K.
Sử dụng kiến thức về định lí cực trị hàm số để giải: Giả sử hàm số \(y = f\left( x \right)\) liên tục trên khoảng (a; b) chứa điểm \({x_0}\) và có đạo hàm trên các khoảng \(\left( {a;{x_0}} \right)\) và \(\left( {{x_0};b} \right)\). Khi đó:
+ Nếu \(f'\left( x \right) < 0\) với mọi \(x \in \left( {a;{x_0}} \right)\) và \(f'\left( x \right) > 0\) với mọi \(x \in \left( {{x_0};b} \right)\) thì điểm \({x_0}\) là một điểm cực tiểu của hàm số f(x).
+ Nếu \(f'\left( x \right) > 0\) với mọi \(x \in \left( {a;{x_0}} \right)\) và \(f'\left( x \right) < 0\) với mọi \(x \in \left( {{x_0};b} \right)\) thì điểm \({x_0}\) là một điểm cực đại của hàm số f(x).
Lời giải chi tiết
a) Vì \(f'\left( x \right) > 0\) khi \(x \in \left( {2;4} \right)\) và \(x \in \left( {6; + \infty } \right)\). Do đó, hàm số f(x) đồng biến trên \(\left( {2;4} \right)\) và \(\left( {6; + \infty } \right)\).
Vì \(f'\left( x \right) < 0\) khi \(x \in \left( {0;2} \right)\) và \(x \in \left( {4;6} \right)\). Do đó, hàm số f(x) nghịch biến trên \(\left( {0;2} \right)\) và \(\left( {4;6} \right)\).
b) Vì \(f'\left( x \right) < 0\) với mọi \(x \in \left( {0;2} \right)\) và \(f'\left( x \right) > 0\) với mọi \(x \in \left( {2;4} \right)\) nên \(x = 2\) là một điểm cực tiểu của hàm số f(x).
Vì \(f'\left( x \right) > 0\) với mọi \(x \in \left( {2;4} \right)\) và \(f'\left( x \right) < 0\) với mọi \(x \in \left( {4;6} \right)\) nên điểm \(x = 4\) là một điểm cực đại của hàm số f(x).
Vì \(f'\left( x \right) < 0\) với mọi \(x \in \left( {4;6} \right)\) và \(f'\left( x \right) > 0\) với mọi \(x \in \left( {6; + \infty } \right)\) nên điểm \(x = 6\) là một điểm cực tiểu của hàm số f(x).
Bài tập 1.6 trang 14 SGK Toán 12 tập 1 - Kết nối tri thức là một bài tập quan trọng trong chương trình học Toán 12, giúp học sinh củng cố kiến thức về giới hạn của hàm số. Để giải bài tập này, học sinh cần nắm vững các khái niệm cơ bản về giới hạn, các định lý về giới hạn và các phương pháp tính giới hạn.
Bài tập 1.6 thường bao gồm các dạng bài tập sau:
Để giúp học sinh hiểu rõ hơn về cách giải bài tập 1.6 trang 14 SGK Toán 12 tập 1, chúng ta sẽ cùng nhau phân tích một số ví dụ cụ thể.
Ví dụ 1: Tính limx→2 (x2 - 4) / (x - 2)
Lời giải:
Ví dụ 2: Tính limx→∞ (2x2 + 3x - 1) / (x2 + 1)
Lời giải:
Kiến thức về giới hạn có ứng dụng rộng rãi trong nhiều lĩnh vực của Toán học và các ngành khoa học khác, như:
Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin hơn khi giải bài tập 1.6 trang 14 SGK Toán 12 tập 1 - Kết nối tri thức và các bài tập tương tự. Chúc các em học tập tốt!