Chào mừng bạn đến với bài học về Lý thuyết Vecto trong không gian, một phần quan trọng của chương trình Toán 12 Kết nối tri thức. Bài học này sẽ cung cấp cho bạn những kiến thức nền tảng và các công cụ cần thiết để giải quyết các bài toán liên quan đến vecto trong không gian.
Chúng ta sẽ cùng nhau khám phá các khái niệm cơ bản, các phép toán trên vecto, và ứng dụng của vecto trong việc giải quyết các bài toán hình học không gian.
1. Vecto trong không gian
1. Vecto trong không gian
Khái niệm vecto trong không gian
- Vecto trong không gian là một đoạn thẳng có hướng - Độ dài của vecto trong không gian là khoảng cách giữa điểm đầu và điểm cuối của vecto đó - Hai vecto được gọi là cùng phương nếu chúng có giá song song hoặc trùng nhau - Nếu hai vecto cùng phương thì chúng cùng hướng hoặc ngược hướng - Hai vecto \(\mathop a\limits^ \to \) và \(\mathop b\limits^ \to \)được gọi là bằng nhau, kí hiệu \(\mathop a\limits^ \to \) = \(\mathop b\limits^ \to \), nếu chúng có cùng độ dài và cùng hướng |
2. Tổng và hiệu của hai vecto trong không gian
a) Tổng của hai vecto trong không gian
Trong không gian, cho hai vecto \(\mathop a\limits^ \to \) và \(\mathop b\limits^ \to \). Lấy một điểm A bất kì và các điểm B,C sao cho \(\overrightarrow {AB} = \overrightarrow a ,\overrightarrow {BC} = \overrightarrow b \). Khi đó, vecto \(\overrightarrow {AC} \) được gọi là tổng của hai vecto \(\mathop a\limits^ \to \) và \(\mathop b\limits^ \to \), kí hiệu là \(\overrightarrow a + \overrightarrow b \) Trong không gian, phép lấy tổng của hai vecto được gọi là phép cộng vecto |
Quy tắc hình hộp
Cho hình hộp ABCD.A’B’C’D’. Khi đó, ta có \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AC'} \) |
b) Hiệu của hai vecto trong không gian
Trong không gian, vecto có cùng độ dài và ngược hướng với vecto \(\mathop a\limits^ \to \) được gọi là vecto đối của vecto \(\mathop a\limits^ \to \), kí hiệu là - \(\mathop a\limits^ \to \) Vecto \(\mathop a\limits^ \to + ( - \mathop b\limits^ \to )\) được gọi là hiệu của hai vecto \(\mathop a\limits^ \to \) và \(\mathop b\limits^ \to \) và kí hiệu là \(\mathop a\limits^ \to - \mathop b\limits^ \to \) Trong không gian, phép lấy hiệu của hai vecto được gọi là phép trừ vecto |
3. Tích của một số với một vecto trong không gian
Trong không gian, tích của một số thực \(k \ne 0\) với một vecto \(\overrightarrow a \ne \overrightarrow 0 \) là một vecto, kí hiệu là \(k\overrightarrow a \), được xác định như sau: - Cùng hướng với vecto \(\mathop a\limits^ \to \) nếu k > 0; ngược hướng với vecto \(\mathop a\limits^ \to \) nếu k < 0 - Có độ dài bằng \(\left| k \right|.\left| {\overrightarrow a } \right|\) Trong không gian, phép lấy tích của một số với một vecto được gọi là phép nhân một số với một vecto |
4. Tích của một số với một vecto trong không gian
a) Góc giữa hai vecto trong không gian
Trong không gian, cho hai vecto \(\mathop a\limits^ \to \) và \(\mathop b\limits^ \to \) khác \(\mathop 0\limits^ \to \). Lấy một điểm O bất kỳ và gọi A, B là hai điểm sao cho \(\overrightarrow {OA} = \overrightarrow a ,\overrightarrow {OB} = \overrightarrow b \). Khi đó, góc \(\widehat {AOB}({0^ \circ } \le \widehat {AOB} \le {180^ \circ })\) được gọi là góc giữa hai vecto \(\mathop a\limits^ \to \) và \(\mathop b\limits^ \to \), kí hiệu \(\left( {\overrightarrow a ,\overrightarrow b } \right)\) |
b) Tích vô hướng của hai vecto trong không gian
Trong không gian, cho hai vecto \(\mathop a\limits^ \to \) và \(\mathop b\limits^ \to \) khác \(\mathop 0\limits^ \to \). Tích vô hướng của hai vecto \(\mathop a\limits^ \to \) và \(\mathop b\limits^ \to \) là một số, kí hiệu là \(\overrightarrow a \cdot \overrightarrow b \), được xác định bởi công thức \(\overrightarrow a \cdot \overrightarrow b = \left| {\overrightarrow a } \right| \cdot \left| {\overrightarrow b } \right| \cdot \cos \left( {\overrightarrow a ,\overrightarrow b } \right)\) |
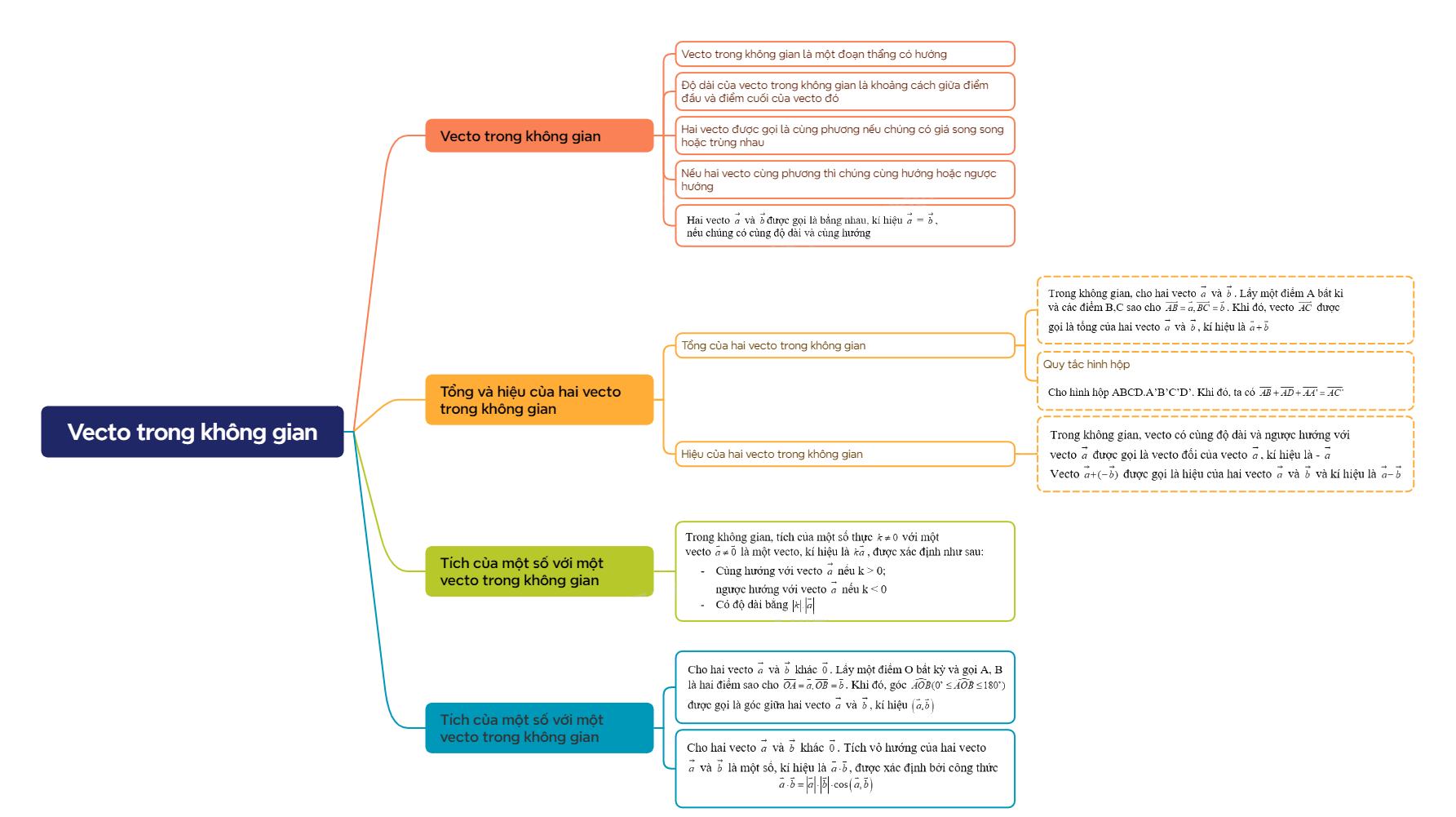
Lý thuyết vecto trong không gian là một phần quan trọng của chương trình Toán 12, đặc biệt trong chương trình Kết nối tri thức. Nó cung cấp nền tảng cho việc giải quyết các bài toán về hình học không gian, đồng thời là công cụ đắc lực trong nhiều lĩnh vực khoa học kỹ thuật.
Vectơ trong không gian là một đoạn thẳng có hướng. Nó được xác định bởi điểm gốc và điểm cuối. Vectơ được ký hiệu là AB, trong đó A là điểm gốc và B là điểm cuối.
Có hai phép toán cơ bản trên vectơ trong không gian là phép cộng và phép nhân với một số thực.
Để cộng hai vectơ a và b, ta sử dụng quy tắc hình bình hành hoặc quy tắc tam giác. Kết quả của phép cộng là một vectơ mới c, sao cho c = a + b.
Quy tắc hình bình hành: Vẽ hình bình hành có hai cạnh là a và b. Đường chéo của hình bình hành xuất phát từ điểm gốc của a là vectơ tổng c.
Quy tắc tam giác: Đặt điểm gốc của b trùng với điểm cuối của a. Vectơ tổng c là vectơ nối điểm gốc của a với điểm cuối của b.
Để nhân một vectơ a với một số thực k, ta thay đổi độ dài của vectơ a thành |k| lần. Nếu k > 0, vectơ mới có cùng hướng với a. Nếu k < 0, vectơ mới ngược hướng với a.
Để thuận tiện cho việc tính toán, ta thường sử dụng hệ tọa độ trong không gian. Một hệ tọa độ trong không gian bao gồm ba trục vuông góc với nhau: trục Ox, trục Oy và trục Oz.
Một vectơ a trong không gian có thể được biểu diễn bằng tọa độ a = (x; y; z), trong đó x, y, z là hình chiếu của vectơ a lên các trục Ox, Oy, Oz.
Các phép toán trên vectơ biểu diễn bằng tọa độ:
Lý thuyết vectơ trong không gian có nhiều ứng dụng trong thực tế, bao gồm:
Bài tập 1: Cho hai điểm A(1; 2; 3) và B(4; 5; 6). Tính độ dài của vectơ AB.
Giải:AB = (4 - 1; 5 - 2; 6 - 3) = (3; 3; 3). Độ dài của vectơ AB là |AB| = √(3² + 3² + 3²) = √27 = 3√3.
Bài tập 2: Cho vectơ a = (1; -2; 3) và b = (2; 1; -1). Tính tích vô hướng của hai vectơ này.
Giải:a.b = (1 * 2) + (-2 * 1) + (3 * -1) = 2 - 2 - 3 = -3.
Hy vọng bài học này đã cung cấp cho bạn những kiến thức cơ bản và hữu ích về Lý thuyết Vecto trong không gian Toán 12 Kết nối tri thức. Chúc bạn học tập tốt!