Bài tập 1.14 trang 19 SGK Toán 12 tập 1 thuộc chương trình học Toán 12 Kết nối tri thức. Bài tập này yêu cầu học sinh vận dụng kiến thức về giới hạn của hàm số để giải quyết các bài toán cụ thể.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập 1.14, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Một nhà sản xuất muốn thiết kế một chiếc hộp có dạng hình hộp chữ nhật không có nắp, có đáy là hình vuông và diện tích bề mặt bằng (108c{m^2}) như Hình 1.17. Tìm các kích thước của chiếc hộp sao cho thể tích của hộp là lớn nhất.
Đề bài
Một nhà sản xuất muốn thiết kế một chiếc hộp có dạng hình hộp chữ nhật không có nắp, có đáy là hình vuông và diện tích bề mặt bằng \(108c{m^2}\) như Hình 1.17. Tìm các kích thước của chiếc hộp sao cho thể tích của hộp là lớn nhất.
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về cách tìm giá trị lớn nhất của hàm số trên một đoạn để tính: Giả sử \(y = f\left( x \right)\) là hàm số liên tục trên \(\left[ {a;b} \right]\) và có đạo hàm trên (a; b), có thể trừ ra tại một số hữu hạn điểm mà tại đó hàm số không có đạo hàm. Giả sử chỉ có hữu hạn điểm trong đoạn \(\left[ {a;b} \right]\) mà đạo hàm \(f'\left( x \right) = 0\).
Các bước tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn \(\left[ {a;b} \right]\):
1. Tìm các điểm \({x_1},{x_2},...{x_n} \in \left( {a;b} \right)\), tại đó \(f'\left( x \right) = 0\) hoặc không tồn tại.
2. Tính \(f\left( {{x_1}} \right);f\left( {{x_2}} \right);...;f\left( {{x_n}} \right)\), f(a) và f(b).
3. Tìm số lớn nhất M và số nhỏ nhất m trong các số trên. Ta có:
\(M = \mathop {\max }\limits_{\left[ {a;b} \right]} f\left( x \right),m = \mathop {\min }\limits_{\left[ {a;b} \right]} f\left( x \right)\)
Lời giải chi tiết
Hình hộp trên có độ dài cạnh đáy là x (cm, \(0 < x < \sqrt {108} \)) và chiều cao là h (cm, \(h > 0\)).
Diện tích bề mặt của hình hộp là \(108c{m^2}\) nên \({x^2} + 4xh = 108 \Rightarrow h = \frac{{108 - {x^2}}}{{4x}}\left( {cm} \right)\).
Thể tích của hình hộp là: \(V = {x^2}.h = {x^2}.\frac{{108 - {x^2}}}{{4x}} = \frac{{108x - {x^3}}}{4}\left( {c{m^3}} \right)\).
Ta có: \(V' = \frac{{ - 3{x^2} + 108}}{4},V' = 0 \Leftrightarrow x = 6\) (do \(x > 0\)).
Bảng biến thiên:
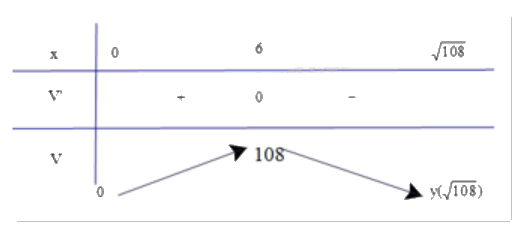
Do đó, thể tích của hình hộp là lớn nhất khi độ dài cạnh đáy \(x = 6\) cm.
Khi đó, chiều cao của hình hộp là: \(\frac{{108 - {6^2}}}{{4.6}} = 3\left( {cm} \right)\).
Bài tập 1.14 SGK Toán 12 tập 1 Kết nối tri thức yêu cầu học sinh tính giới hạn của hàm số khi x tiến tới một giá trị nhất định. Để giải bài tập này, chúng ta cần nắm vững các định nghĩa và tính chất của giới hạn hàm số, cũng như các quy tắc tính giới hạn.
Trước khi bắt đầu giải bài tập, chúng ta cần đọc kỹ đề bài để hiểu rõ yêu cầu. Xác định hàm số cần tính giới hạn và giá trị mà x tiến tới. Sau đó, lựa chọn phương pháp giải phù hợp. Các phương pháp thường được sử dụng bao gồm:
Bài tập: Tính các giới hạn sau:
1. lim (x→2) (x^2 - 4) / (x - 2)
Ta có: (x^2 - 4) / (x - 2) = (x - 2)(x + 2) / (x - 2) = x + 2 (với x ≠ 2)
Vậy, lim (x→2) (x^2 - 4) / (x - 2) = lim (x→2) (x + 2) = 2 + 2 = 4
2. lim (x→1) (x^3 - 1) / (x - 1)
Ta có: x^3 - 1 = (x - 1)(x^2 + x + 1)
Vậy, lim (x→1) (x^3 - 1) / (x - 1) = lim (x→1) (x^2 + x + 1) = 1^2 + 1 + 1 = 3
3. lim (x→0) (√(x+1) - 1) / x
Nhân tử số và mẫu số với liên hợp của √(x+1) - 1 là √(x+1) + 1, ta được:
(√(x+1) - 1) / x = ((√(x+1) - 1)(√(x+1) + 1)) / (x(√(x+1) + 1)) = (x+1 - 1) / (x(√(x+1) + 1)) = x / (x(√(x+1) + 1)) = 1 / (√(x+1) + 1) (với x ≠ 0)
Vậy, lim (x→0) (√(x+1) - 1) / x = lim (x→0) 1 / (√(x+1) + 1) = 1 / (√(0+1) + 1) = 1 / 2
Thông qua việc giải bài tập 1.14, chúng ta đã củng cố kiến thức về giới hạn hàm số và các phương pháp tính giới hạn. Việc luyện tập thường xuyên sẽ giúp các em học sinh nắm vững kiến thức và tự tin giải quyết các bài toán tương tự.
Ngoài bài tập 1.14, các em có thể tham khảo thêm các bài tập khác trong SGK Toán 12 tập 1 Kết nối tri thức để nâng cao kiến thức và kỹ năng giải toán. Bên cạnh đó, các em cũng có thể tìm kiếm các tài liệu học tập trực tuyến, các video hướng dẫn giải bài tập trên các trang web như giaitoan.edu.vn để có thêm nguồn tham khảo.
Việc học Toán 12 đòi hỏi sự kiên trì và nỗ lực. Hãy dành thời gian ôn tập và luyện tập thường xuyên để đạt kết quả tốt nhất.