Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 tập 1 Kết nối tri thức tại giaitoan.edu.vn. Chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho từng bài tập trong SGK, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Mục 1 của chương trình Toán 12 tập 1 tập trung vào các kiến thức cơ bản về giới hạn dãy số, giới hạn hàm số. Việc hiểu rõ các khái niệm này là nền tảng quan trọng để giải quyết các bài toán phức tạp hơn trong chương trình.
Định nghĩa
Trả lời câu hỏi Hoạt động 1 trang 15 SGK Toán 12 Kết nối tri thức
Cho hàm số \(y = f\left( x \right) = {x^2} - 2x\) với \(x \in \left[ {0;3} \right]\), có đồ thị như Hình 1.15.
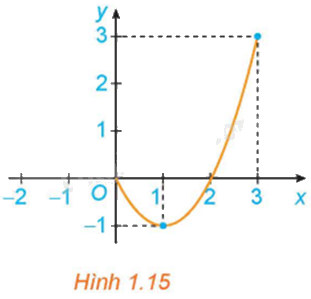
a) Giá trị lớn nhất M của hàm số trên đoạn \(\left[ {0;3} \right]\) là bao nhiêu? Tìm \({x_0}\) sao cho \(f\left( {{x_0}} \right) = M\).
b) Giá trị nhỏ nhất m của hàm số trên đoạn \(\left[ {0;3} \right]\) là bao nhiêu? Tìm \({x_0}\) sao cho \(f\left( {{x_0}} \right) = m\).
Phương pháp giải:
Sử dụng kiến thức về đọc hiểu đồ thị hàm số.
Lời giải chi tiết:
a) Giá trị lớn nhất của đồ thị hàm số trên đoạn \(\left[ {0;3} \right]\) là \(M = 3\).
Với \({x_0} = 3\) thì \(f\left( 3 \right) = 3\).
b) Giá trị nhỏ nhất của đồ thị hàm số trên đoạn \(\left[ {0;3} \right]\) là \(m = - 1\).
Với \({x_0} = 1\) thì \(f\left( 1 \right) = - 1\).
Trả lời câu hỏi Luyện tập 1 trang 17 SGK Toán 12 Kết nối tri thức
Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau:
a) \(y = \sqrt {2x - {x^2}} \);
b) \(y = - x + \frac{1}{{x - 1}}\) trên khoảng \(\left( {1; + \infty } \right)\).
Phương pháp giải:
Sử dụng kiến thức về khái niệm giá trị lớn nhất, giá trị nhỏ nhất của hàm số để tính: Cho hàm số \(y = f\left( x \right)\) xác định trên tập D.
+ Số M được gọi là giá trị lớn nhất của hàm số \(y = f\left( x \right)\) trên tập D nếu \(f\left( x \right) \le M\) với mọi \(x \in D\) và tồn tại \({x_0} \in D\) sao cho \(f\left( {{x_0}} \right) = M\).
Kí hiệu \(M = \mathop {\max }\limits_{x \in D} f\left( x \right)\) hoặc \(M = \mathop {\max }\limits_D f\left( x \right)\)
+ Số m được gọi là giá trị nhỏ nhất của hàm số \(y = f\left( x \right)\) trên tập D nếu \(f\left( x \right) \ge m\) với mọi \(x \in D\) và tồn tại \({x_0} \in D\) sao cho \(f\left( {{x_0}} \right) = m\).
Kí hiệu \(m = \mathop {\min }\limits_{x \in D} f\left( x \right)\) hoặc \(m = \mathop {\min }\limits_D f\left( x \right)\)
Lời giải chi tiết:
a) Tập xác định của hàm số là \(\left[ {0;2} \right]\).
Với \(x \in \left[ {0;2} \right]\) ta có: \(y' = \frac{{\left( {2x - {x^2}} \right)'}}{{2\sqrt {2x - {x^2}} }} = \frac{{ - x + 1}}{{\sqrt {2x - {x^2}} }}\), \(y' = 0 \Leftrightarrow \frac{{ - x + 1}}{{\sqrt {2x - {x^2}} }} = 0 \Leftrightarrow x = 1\left( {tm} \right)\)
Lập bảng biến thiên của hàm số trên đoạn \(\left[ {0;2} \right]\):
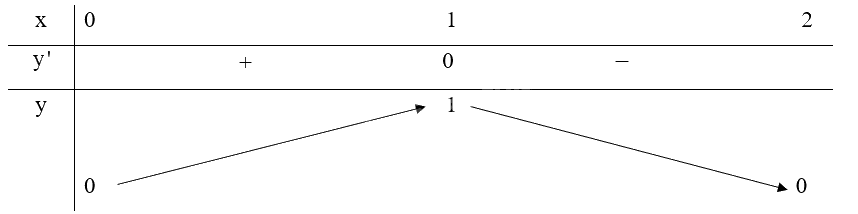
Từ bảng biến thiên ta thấy: \(\mathop {\min }\limits_{\left[ { - 1;1} \right]} f\left( x \right) = f\left( 0 \right) = f\left( 2 \right) = 0,\mathop {\max }\limits_{\left[ { - 1;1} \right]} f\left( x \right) = f\left( 1 \right) = 1\).
b) Với \(x \in \left( {1; + \infty } \right)\) ta có:
Ta có: \(y' = - 1 + \frac{{ - 1}}{{{{\left( {x - 1} \right)}^2}}} < 0\;\forall x \in \left( {1; + \infty } \right)\)
\(\mathop {\lim }\limits_{x \to {1^ + }} y = \mathop {\lim }\limits_{x \to {1^ + }} \left( { - x + \frac{1}{{x - 1}}} \right) = + \infty ;\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \left( { - x + \frac{1}{{x - 1}}} \right) = - \infty \)
Lập bảng biến thiên của hàm số trên \(\left( {1; + \infty } \right)\):
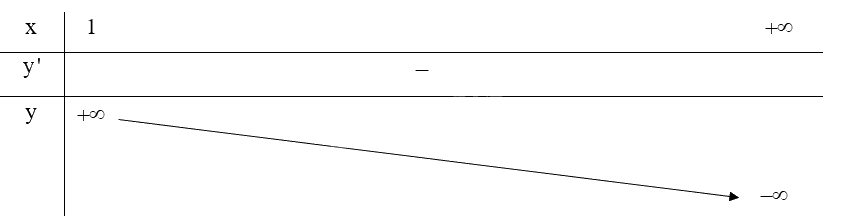
Vậy hàm số không có giá trị lớn nhất, giá trị nhỏ nhất trên \(\left( {1; + \infty } \right)\).
Trả lời câu hỏi Hoạt động 1 trang 15 SGK Toán 12 Kết nối tri thức
Cho hàm số \(y = f\left( x \right) = {x^2} - 2x\) với \(x \in \left[ {0;3} \right]\), có đồ thị như Hình 1.15.
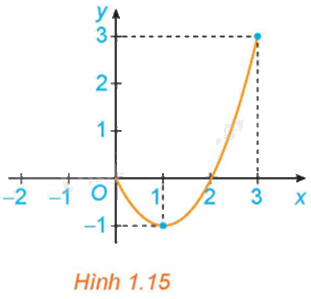
a) Giá trị lớn nhất M của hàm số trên đoạn \(\left[ {0;3} \right]\) là bao nhiêu? Tìm \({x_0}\) sao cho \(f\left( {{x_0}} \right) = M\).
b) Giá trị nhỏ nhất m của hàm số trên đoạn \(\left[ {0;3} \right]\) là bao nhiêu? Tìm \({x_0}\) sao cho \(f\left( {{x_0}} \right) = m\).
Phương pháp giải:
Sử dụng kiến thức về đọc hiểu đồ thị hàm số.
Lời giải chi tiết:
a) Giá trị lớn nhất của đồ thị hàm số trên đoạn \(\left[ {0;3} \right]\) là \(M = 3\).
Với \({x_0} = 3\) thì \(f\left( 3 \right) = 3\).
b) Giá trị nhỏ nhất của đồ thị hàm số trên đoạn \(\left[ {0;3} \right]\) là \(m = - 1\).
Với \({x_0} = 1\) thì \(f\left( 1 \right) = - 1\).
Trả lời câu hỏi Luyện tập 1 trang 17 SGK Toán 12 Kết nối tri thức
Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau:
a) \(y = \sqrt {2x - {x^2}} \);
b) \(y = - x + \frac{1}{{x - 1}}\) trên khoảng \(\left( {1; + \infty } \right)\).
Phương pháp giải:
Sử dụng kiến thức về khái niệm giá trị lớn nhất, giá trị nhỏ nhất của hàm số để tính: Cho hàm số \(y = f\left( x \right)\) xác định trên tập D.
+ Số M được gọi là giá trị lớn nhất của hàm số \(y = f\left( x \right)\) trên tập D nếu \(f\left( x \right) \le M\) với mọi \(x \in D\) và tồn tại \({x_0} \in D\) sao cho \(f\left( {{x_0}} \right) = M\).
Kí hiệu \(M = \mathop {\max }\limits_{x \in D} f\left( x \right)\) hoặc \(M = \mathop {\max }\limits_D f\left( x \right)\)
+ Số m được gọi là giá trị nhỏ nhất của hàm số \(y = f\left( x \right)\) trên tập D nếu \(f\left( x \right) \ge m\) với mọi \(x \in D\) và tồn tại \({x_0} \in D\) sao cho \(f\left( {{x_0}} \right) = m\).
Kí hiệu \(m = \mathop {\min }\limits_{x \in D} f\left( x \right)\) hoặc \(m = \mathop {\min }\limits_D f\left( x \right)\)
Lời giải chi tiết:
a) Tập xác định của hàm số là \(\left[ {0;2} \right]\).
Với \(x \in \left[ {0;2} \right]\) ta có: \(y' = \frac{{\left( {2x - {x^2}} \right)'}}{{2\sqrt {2x - {x^2}} }} = \frac{{ - x + 1}}{{\sqrt {2x - {x^2}} }}\), \(y' = 0 \Leftrightarrow \frac{{ - x + 1}}{{\sqrt {2x - {x^2}} }} = 0 \Leftrightarrow x = 1\left( {tm} \right)\)
Lập bảng biến thiên của hàm số trên đoạn \(\left[ {0;2} \right]\):
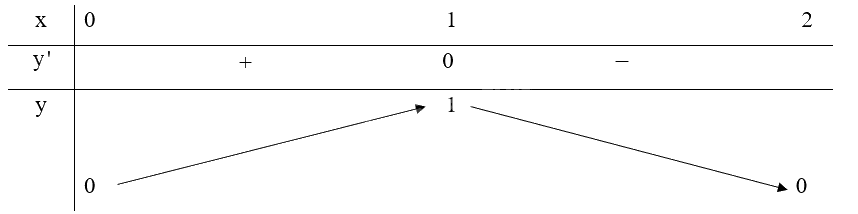
Từ bảng biến thiên ta thấy: \(\mathop {\min }\limits_{\left[ { - 1;1} \right]} f\left( x \right) = f\left( 0 \right) = f\left( 2 \right) = 0,\mathop {\max }\limits_{\left[ { - 1;1} \right]} f\left( x \right) = f\left( 1 \right) = 1\).
b) Với \(x \in \left( {1; + \infty } \right)\) ta có:
Ta có: \(y' = - 1 + \frac{{ - 1}}{{{{\left( {x - 1} \right)}^2}}} < 0\;\forall x \in \left( {1; + \infty } \right)\)
\(\mathop {\lim }\limits_{x \to {1^ + }} y = \mathop {\lim }\limits_{x \to {1^ + }} \left( { - x + \frac{1}{{x - 1}}} \right) = + \infty ;\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \left( { - x + \frac{1}{{x - 1}}} \right) = - \infty \)
Lập bảng biến thiên của hàm số trên \(\left( {1; + \infty } \right)\):
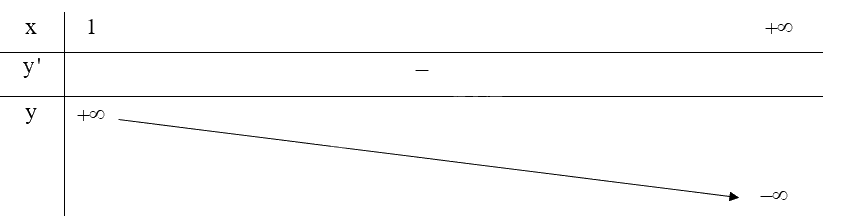
Vậy hàm số không có giá trị lớn nhất, giá trị nhỏ nhất trên \(\left( {1; + \infty } \right)\).
Mục 1 của SGK Toán 12 tập 1 Kết nối tri thức giới thiệu về khái niệm giới hạn của dãy số và hàm số. Đây là một trong những khái niệm nền tảng của giải tích, đóng vai trò quan trọng trong việc hiểu và giải quyết các bài toán liên quan đến sự thay đổi và xu hướng của các đại lượng.
Dãy số (un) được gọi là có giới hạn L nếu khi n tiến tới vô cùng, các số hạng của dãy số tiến gần đến L. Ký hiệu: limn→∞ un = L.
Hàm số f(x) được gọi là có giới hạn L khi x tiến tới a nếu khi x tiến gần đến a, các giá trị của f(x) tiến gần đến L. Ký hiệu: limx→a f(x) = L.
Bài 1: Tính limn→∞ (2n + 1) / (n - 3)
Lời giải:
limn→∞ (2n + 1) / (n - 3) = limn→∞ (2 + 1/n) / (1 - 3/n) = (2 + 0) / (1 - 0) = 2
Bài 2: Tính limx→2 (x2 - 4) / (x - 2)
Lời giải:
limx→2 (x2 - 4) / (x - 2) = limx→2 (x - 2)(x + 2) / (x - 2) = limx→2 (x + 2) = 2 + 2 = 4
Khái niệm giới hạn có ứng dụng rộng rãi trong nhiều lĩnh vực của khoa học và kỹ thuật, như:
Hy vọng với những kiến thức và phương pháp giải bài tập về giới hạn được trình bày trên đây, các em học sinh sẽ tự tin hơn trong việc học tập và giải quyết các bài toán liên quan đến giới hạn dãy số và hàm số.