Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 tập 1 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 3 trang 52, 53, 54 sách giáo khoa Toán 12 tập 1 - Kết nối tri thức.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong môn học Toán.
Tích của một số với một vectơ trong không gian
Trả lời câu hỏi Câu hỏi trang 53 SGK Toán 12 Kết nối tri thức
Hai vectơ \(1\overrightarrow a \) và \(\overrightarrow a \) có bằng nhau không? Hai vectơ \(\left( { - 1} \right)\overrightarrow a \) và \( - \overrightarrow a \) có bằng nhau không?
Phương pháp giải:
Sử dụng kiến thức về hai vectơ bằng nhau để chứng minh: Hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) được gọi là bằng nhau, kí hiệu \(\overrightarrow a = \overrightarrow b \) nếu chúng có cùng độ dài và cùng hướng.
Lời giải chi tiết:
Hai vectơ \(1\overrightarrow a \) và \(\overrightarrow a \) bằng nhau vì chúng có cùng độ dài và cùng hướng.
Hai vectơ \(\left( { - 1} \right)\overrightarrow a \) và \( - \overrightarrow a \) bằng nhau chúng có cùng độ dài và cùng hướng.
Trả lời câu hỏi Hoạt động 6 trang 52 SGK Toán 12 Kết nối tri thức
Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi M, N lần lượt là trung điểm của AB, AC (H.2.17)
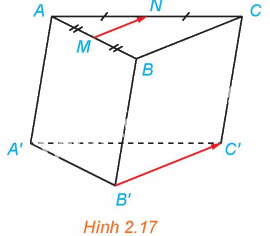
a) Hai vectơ \(\overrightarrow {MN} \) và \(\overrightarrow {B'C'} \) có cùng phương không? Có cùng hướng không?
b) Giải thích vì sao \(\left| {\overrightarrow {MN} } \right| = \frac{1}{2}\left| {\overrightarrow {B'C'} } \right|\).
Phương pháp giải:
a) Sử dụng kiến thức về hai vectơ cùng phương để chứng minh: Hai vectơ được gọi là cùng phương nếu chúng có giá song song hoặc trùng nhau.
b) Sử dụng kiến thức về độ dài của vectơ trong không gian để chứng minh: Độ dài của vectơ trong không gian là khoảng cách giữa điểm đầu và điểm cuối của vectơ đó. Độ dài của vectơ \(\overrightarrow a \) được kí hiệu là \(\left| {\overrightarrow a } \right|\).
Lời giải chi tiết:
a) Vì MN là đường trung bình của tam giác ABC nên MN//BC.
Vì BCC’B’ là hình bình hành nên BC//B’C’. Suy ra: MN//B’C’.
Do đó hai vectơ \(\overrightarrow {MN} \) và \(\overrightarrow {B'C'} \) có cùng phương và cùng hướng.
b) Vì BCC’B’ là hình bình hành nên \(BC = B'C'\)
Vì MN là đường trung bình của tam giác ABC nên \(MN = \frac{1}{2}BC\)
Suy ra: \(\left| {\overrightarrow {MN} } \right| = \frac{1}{2}\left| {\overrightarrow {B'C'} } \right|\).
Trả lời câu hỏi Luyện tập 7 trang 53SGK Toán 12 Kết nối tri thức
Cho hình chóp S. ABCD có đáy ABCD là hình bình hành. Gọi E, F lần lượt là các điểm thuộc các cạnh SA, SB sao cho \(SE = \frac{1}{3}SA,SF = \frac{1}{3}SB\). Chứng minh rằng \(\overrightarrow {EF} = \frac{1}{3}\overrightarrow {DC} \).
Phương pháp giải:
+ Sử dụng kiến thức về khái niệm tích của một số với một vectơ trong không gian để chứng minh: Trong không gian, tích của một số thực \(k \ne 0\) với một vectơ \(\overrightarrow a \ne \overrightarrow 0 \) là một vectơ, kí hiệu là \(k\overrightarrow a \) được xác định như sau:
- Cùng hướng với vectơ \(\overrightarrow a \) nếu \(k > 0\), ngược hướng với vectơ \(\overrightarrow a \) nếu \(k < 0\).
- Có độ dài bằng \(\left| k \right|\left| {\overrightarrow a } \right|\).
+ Sử dụng kiến thức về hai vectơ bằng nhau để chứng minh: Hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) được gọi là bằng nhau, kí hiệu \(\overrightarrow a = \overrightarrow b \) nếu chúng có cùng độ dài và cùng hướng.
Lời giải chi tiết:
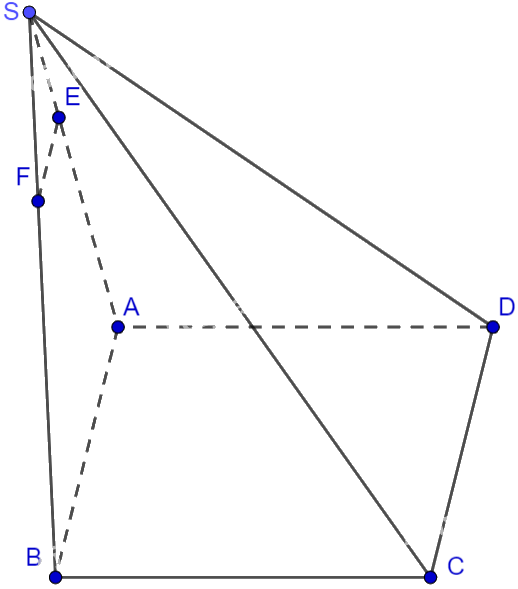
Vì \(SE = \frac{1}{3}SA,SF = \frac{1}{3}SB \Rightarrow \frac{{SE}}{{SA}} = \frac{{SF}}{{SB}}\left( { = \frac{1}{3}} \right)\)
Tam giác SAB có: \(\frac{{SE}}{{SA}} = \frac{{SF}}{{SB}}\) nên FE//AB và \(EF = \frac{1}{3}AB\).
Vì hai vectơ \(\overrightarrow {EF} \) và \(\overrightarrow {AB} \) cùng hướng nên \(\overrightarrow {EF} = \frac{1}{3}\overrightarrow {AB} \) (1)
Vì ABCD là hình bình hành nên \(AB = CD\) và AB//CD. Do đó, \(\overrightarrow {AB} = \overrightarrow {DC} \) (2)
Từ (1) và (2) ta có: \(\overrightarrow {EF} = \frac{1}{3}\overrightarrow {DC} \)
Trả lời câu hỏi Luyện tập 8 trang 54SGK Toán 12 Kết nối tri thức
Trong Ví dụ 8, gọi I là điểm thuộc đoạn thẳng AG sao cho \(\overrightarrow {AI} = 3\overrightarrow {IG} \) (H.2.19). Chứng minh rằng \(\overrightarrow {IA} + \overrightarrow {IB} + \overrightarrow {IC} + \overrightarrow {ID} = \overrightarrow 0 \).
Phương pháp giải:
Sử dụng kiến thức về khái niệm tích của một số với một vectơ trong không gian để chứng minh: Trong không gian, tích của một số thực \(k \ne 0\) với một vectơ \(\overrightarrow a \ne \overrightarrow 0 \) là một vectơ, kí hiệu là \(k\overrightarrow a \) được xác định như sau:
- Cùng hướng với vectơ \(\overrightarrow a \) nếu \(k > 0\), ngược hướng với vectơ \(\overrightarrow a \) nếu \(k < 0\).
- Có độ dài bằng \(\left| k \right|\left| {\overrightarrow a } \right|\).
Lời giải chi tiết:
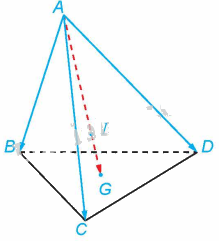
Theo ví dụ 8 ta có: \(\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} = 3\overrightarrow {AG} \)\( \Rightarrow \overrightarrow {AI} + \overrightarrow {IB} + \overrightarrow {AI} + \overrightarrow {IC} + \overrightarrow {AI} + \overrightarrow {ID} = 3\overrightarrow {AG} \)
\( \Rightarrow \overrightarrow {IB} + \overrightarrow {IC} + \overrightarrow {ID} = 3\overrightarrow {AG} - 3\overrightarrow {AI} = 3\left( {\overrightarrow {AG} + \overrightarrow {IA} } \right) = 3\overrightarrow {IG} = \overrightarrow {AI} \)\( \Rightarrow \overrightarrow {IA} + \overrightarrow {IB} + \overrightarrow {IC} + \overrightarrow {ID} = \overrightarrow 0 \)
Trả lời câu hỏi Vận dụng 8 trang 54SGK Toán 12 Kết nối tri thức
Khi chuyển động trong không gian, máy bay luôn chịu tác động của bốn lực chính: lực đẩy của động cơ, lực cản của không khí, trọng lực và lực nâng khí động học (H.2.20). Lực cản của không khí ngược hướng với lực đẩy của động cơ và có độ lớn tỉ lệ thuận với bình phương vận tốc máy bay. Một chiếc máy bay tăng vận tốc từ 900km/h lên 920km/h, trong quá trình tăng tốc máy bay giữ nguyên hướng bay. Lực cản của không khí khi máy bay đạt vận tốc 900km/h và 920km/h lần lượt được biểu diễn bởi hai vectơ \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \). Hãy giải thích vì sao \(\overrightarrow {{F_1}} = k\overrightarrow {{F_2}} \) với k là một số thực dương nào đó. Tính giá trị của k (làm tròn kết quả đến chữ số thập phân thứ hai).

Phương pháp giải:
Sử dụng kiến thức về khái niệm tích của một số với một vectơ trong không gian để giải bài toán: Trong không gian, tích của một số thực \(k \ne 0\) với một vectơ \(\overrightarrow a \ne \overrightarrow 0 \) là một vectơ, kí hiệu là \(k\overrightarrow a \) được xác định như sau:
- Cùng hướng với vectơ \(\overrightarrow a \) nếu \(k > 0\), ngược hướng với vectơ \(\overrightarrow a \) nếu \(k < 0\).
- Có độ dài bằng \(\left| k \right|\left| {\overrightarrow a } \right|\).
Lời giải chi tiết:
Vì trong quá trình máy bay tăng vận tốc từ 900km/h lên 920km/h máy bay giữ nguyên hướng bay nên vectơ \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) có cùng hướng. Do đó, \(\overrightarrow {{F_1}} = k\overrightarrow {{F_2}} \) với k là một số thực dương nào đó (1).
Gọi \({v_1},{v_2}\) lần lượt là vận tốc của của chiếc máy bay khi đạt 900km/h và 920km/h.
Suy ra \({v_1} = 900\left( {km/h} \right),{v_2} = 920\left( {km/h} \right)\)
Vì lực cản của không khí ngược hướng với lực đẩy của động cơ và có độ lớn tỉ lệ thuận với bình phương vận tốc máy bay nên
\(\frac{{\left| {\overrightarrow {{F_1}} } \right|}}{{\left| {\overrightarrow {{F_2}} } \right|}} = \frac{{v_1^2}}{{v_2^2}} = \frac{{{{900}^2}}}{{{{920}^2}}} = \frac{{2025}}{{2116}} \Rightarrow \left| {\overrightarrow {{F_1}} } \right| = \frac{{2025}}{{2116}}\left| {\overrightarrow {{F_2}} } \right|\) (2)
Từ (1) và (2) ta có: \(\overrightarrow {{F_1}} = \frac{{2025}}{{2116}}\overrightarrow {{F_2}} \Rightarrow k = \frac{{2025}}{{2116}} \approx 0,96\)
Trả lời câu hỏi Hoạt động 6 trang 52 SGK Toán 12 Kết nối tri thức
Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi M, N lần lượt là trung điểm của AB, AC (H.2.17)
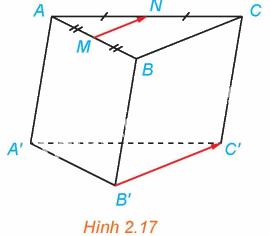
a) Hai vectơ \(\overrightarrow {MN} \) và \(\overrightarrow {B'C'} \) có cùng phương không? Có cùng hướng không?
b) Giải thích vì sao \(\left| {\overrightarrow {MN} } \right| = \frac{1}{2}\left| {\overrightarrow {B'C'} } \right|\).
Phương pháp giải:
a) Sử dụng kiến thức về hai vectơ cùng phương để chứng minh: Hai vectơ được gọi là cùng phương nếu chúng có giá song song hoặc trùng nhau.
b) Sử dụng kiến thức về độ dài của vectơ trong không gian để chứng minh: Độ dài của vectơ trong không gian là khoảng cách giữa điểm đầu và điểm cuối của vectơ đó. Độ dài của vectơ \(\overrightarrow a \) được kí hiệu là \(\left| {\overrightarrow a } \right|\).
Lời giải chi tiết:
a) Vì MN là đường trung bình của tam giác ABC nên MN//BC.
Vì BCC’B’ là hình bình hành nên BC//B’C’. Suy ra: MN//B’C’.
Do đó hai vectơ \(\overrightarrow {MN} \) và \(\overrightarrow {B'C'} \) có cùng phương và cùng hướng.
b) Vì BCC’B’ là hình bình hành nên \(BC = B'C'\)
Vì MN là đường trung bình của tam giác ABC nên \(MN = \frac{1}{2}BC\)
Suy ra: \(\left| {\overrightarrow {MN} } \right| = \frac{1}{2}\left| {\overrightarrow {B'C'} } \right|\).
Trả lời câu hỏi Câu hỏi trang 53 SGK Toán 12 Kết nối tri thức
Hai vectơ \(1\overrightarrow a \) và \(\overrightarrow a \) có bằng nhau không? Hai vectơ \(\left( { - 1} \right)\overrightarrow a \) và \( - \overrightarrow a \) có bằng nhau không?
Phương pháp giải:
Sử dụng kiến thức về hai vectơ bằng nhau để chứng minh: Hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) được gọi là bằng nhau, kí hiệu \(\overrightarrow a = \overrightarrow b \) nếu chúng có cùng độ dài và cùng hướng.
Lời giải chi tiết:
Hai vectơ \(1\overrightarrow a \) và \(\overrightarrow a \) bằng nhau vì chúng có cùng độ dài và cùng hướng.
Hai vectơ \(\left( { - 1} \right)\overrightarrow a \) và \( - \overrightarrow a \) bằng nhau chúng có cùng độ dài và cùng hướng.
Trả lời câu hỏi Luyện tập 7 trang 53SGK Toán 12 Kết nối tri thức
Cho hình chóp S. ABCD có đáy ABCD là hình bình hành. Gọi E, F lần lượt là các điểm thuộc các cạnh SA, SB sao cho \(SE = \frac{1}{3}SA,SF = \frac{1}{3}SB\). Chứng minh rằng \(\overrightarrow {EF} = \frac{1}{3}\overrightarrow {DC} \).
Phương pháp giải:
+ Sử dụng kiến thức về khái niệm tích của một số với một vectơ trong không gian để chứng minh: Trong không gian, tích của một số thực \(k \ne 0\) với một vectơ \(\overrightarrow a \ne \overrightarrow 0 \) là một vectơ, kí hiệu là \(k\overrightarrow a \) được xác định như sau:
- Cùng hướng với vectơ \(\overrightarrow a \) nếu \(k > 0\), ngược hướng với vectơ \(\overrightarrow a \) nếu \(k < 0\).
- Có độ dài bằng \(\left| k \right|\left| {\overrightarrow a } \right|\).
+ Sử dụng kiến thức về hai vectơ bằng nhau để chứng minh: Hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) được gọi là bằng nhau, kí hiệu \(\overrightarrow a = \overrightarrow b \) nếu chúng có cùng độ dài và cùng hướng.
Lời giải chi tiết:
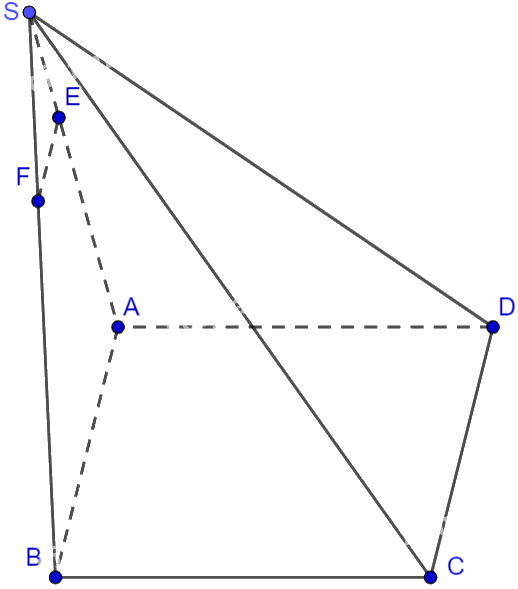
Vì \(SE = \frac{1}{3}SA,SF = \frac{1}{3}SB \Rightarrow \frac{{SE}}{{SA}} = \frac{{SF}}{{SB}}\left( { = \frac{1}{3}} \right)\)
Tam giác SAB có: \(\frac{{SE}}{{SA}} = \frac{{SF}}{{SB}}\) nên FE//AB và \(EF = \frac{1}{3}AB\).
Vì hai vectơ \(\overrightarrow {EF} \) và \(\overrightarrow {AB} \) cùng hướng nên \(\overrightarrow {EF} = \frac{1}{3}\overrightarrow {AB} \) (1)
Vì ABCD là hình bình hành nên \(AB = CD\) và AB//CD. Do đó, \(\overrightarrow {AB} = \overrightarrow {DC} \) (2)
Từ (1) và (2) ta có: \(\overrightarrow {EF} = \frac{1}{3}\overrightarrow {DC} \)
Trả lời câu hỏi Luyện tập 8 trang 54SGK Toán 12 Kết nối tri thức
Trong Ví dụ 8, gọi I là điểm thuộc đoạn thẳng AG sao cho \(\overrightarrow {AI} = 3\overrightarrow {IG} \) (H.2.19). Chứng minh rằng \(\overrightarrow {IA} + \overrightarrow {IB} + \overrightarrow {IC} + \overrightarrow {ID} = \overrightarrow 0 \).
Phương pháp giải:
Sử dụng kiến thức về khái niệm tích của một số với một vectơ trong không gian để chứng minh: Trong không gian, tích của một số thực \(k \ne 0\) với một vectơ \(\overrightarrow a \ne \overrightarrow 0 \) là một vectơ, kí hiệu là \(k\overrightarrow a \) được xác định như sau:
- Cùng hướng với vectơ \(\overrightarrow a \) nếu \(k > 0\), ngược hướng với vectơ \(\overrightarrow a \) nếu \(k < 0\).
- Có độ dài bằng \(\left| k \right|\left| {\overrightarrow a } \right|\).
Lời giải chi tiết:
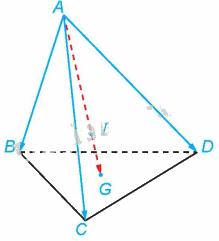
Theo ví dụ 8 ta có: \(\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} = 3\overrightarrow {AG} \)\( \Rightarrow \overrightarrow {AI} + \overrightarrow {IB} + \overrightarrow {AI} + \overrightarrow {IC} + \overrightarrow {AI} + \overrightarrow {ID} = 3\overrightarrow {AG} \)
\( \Rightarrow \overrightarrow {IB} + \overrightarrow {IC} + \overrightarrow {ID} = 3\overrightarrow {AG} - 3\overrightarrow {AI} = 3\left( {\overrightarrow {AG} + \overrightarrow {IA} } \right) = 3\overrightarrow {IG} = \overrightarrow {AI} \)\( \Rightarrow \overrightarrow {IA} + \overrightarrow {IB} + \overrightarrow {IC} + \overrightarrow {ID} = \overrightarrow 0 \)
Trả lời câu hỏi Vận dụng 8 trang 54SGK Toán 12 Kết nối tri thức
Khi chuyển động trong không gian, máy bay luôn chịu tác động của bốn lực chính: lực đẩy của động cơ, lực cản của không khí, trọng lực và lực nâng khí động học (H.2.20). Lực cản của không khí ngược hướng với lực đẩy của động cơ và có độ lớn tỉ lệ thuận với bình phương vận tốc máy bay. Một chiếc máy bay tăng vận tốc từ 900km/h lên 920km/h, trong quá trình tăng tốc máy bay giữ nguyên hướng bay. Lực cản của không khí khi máy bay đạt vận tốc 900km/h và 920km/h lần lượt được biểu diễn bởi hai vectơ \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \). Hãy giải thích vì sao \(\overrightarrow {{F_1}} = k\overrightarrow {{F_2}} \) với k là một số thực dương nào đó. Tính giá trị của k (làm tròn kết quả đến chữ số thập phân thứ hai).

Phương pháp giải:
Sử dụng kiến thức về khái niệm tích của một số với một vectơ trong không gian để giải bài toán: Trong không gian, tích của một số thực \(k \ne 0\) với một vectơ \(\overrightarrow a \ne \overrightarrow 0 \) là một vectơ, kí hiệu là \(k\overrightarrow a \) được xác định như sau:
- Cùng hướng với vectơ \(\overrightarrow a \) nếu \(k > 0\), ngược hướng với vectơ \(\overrightarrow a \) nếu \(k < 0\).
- Có độ dài bằng \(\left| k \right|\left| {\overrightarrow a } \right|\).
Lời giải chi tiết:
Vì trong quá trình máy bay tăng vận tốc từ 900km/h lên 920km/h máy bay giữ nguyên hướng bay nên vectơ \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) có cùng hướng. Do đó, \(\overrightarrow {{F_1}} = k\overrightarrow {{F_2}} \) với k là một số thực dương nào đó (1).
Gọi \({v_1},{v_2}\) lần lượt là vận tốc của của chiếc máy bay khi đạt 900km/h và 920km/h.
Suy ra \({v_1} = 900\left( {km/h} \right),{v_2} = 920\left( {km/h} \right)\)
Vì lực cản của không khí ngược hướng với lực đẩy của động cơ và có độ lớn tỉ lệ thuận với bình phương vận tốc máy bay nên
\(\frac{{\left| {\overrightarrow {{F_1}} } \right|}}{{\left| {\overrightarrow {{F_2}} } \right|}} = \frac{{v_1^2}}{{v_2^2}} = \frac{{{{900}^2}}}{{{{920}^2}}} = \frac{{2025}}{{2116}} \Rightarrow \left| {\overrightarrow {{F_1}} } \right| = \frac{{2025}}{{2116}}\left| {\overrightarrow {{F_2}} } \right|\) (2)
Từ (1) và (2) ta có: \(\overrightarrow {{F_1}} = \frac{{2025}}{{2116}}\overrightarrow {{F_2}} \Rightarrow k = \frac{{2025}}{{2116}} \approx 0,96\)
Mục 3 trong SGK Toán 12 tập 1 - Kết nối tri thức tập trung vào việc nghiên cứu về giới hạn của hàm số tại một điểm và giới hạn vô cùng. Đây là một trong những khái niệm nền tảng quan trọng trong chương trình Toán học lớp 12, đóng vai trò then chốt trong việc hiểu và giải quyết các bài toán về đạo hàm, tích phân và các ứng dụng của chúng.
Mục 3 được chia thành các phần chính sau:
Trang 52 SGK Toán 12 tập 1 - Kết nối tri thức chứa các bài tập về giới hạn của hàm số tại một điểm. Các bài tập này yêu cầu các em áp dụng định nghĩa và các tính chất của giới hạn để tính toán giá trị giới hạn của hàm số.
Ví dụ, bài tập 1 yêu cầu tính giới hạn của hàm số f(x) = (x^2 - 1) / (x - 1) khi x tiến tới 1. Để giải bài tập này, các em có thể phân tích tử số thành nhân tử và rút gọn biểu thức, sau đó thay x = 1 vào biểu thức rút gọn để tính giá trị giới hạn.
Trang 53 SGK Toán 12 tập 1 - Kết nối tri thức chứa các bài tập về giới hạn vô cùng. Các bài tập này yêu cầu các em tính giới hạn của hàm số khi x tiến tới vô cùng dương hoặc vô cùng âm.
Ví dụ, bài tập 2 yêu cầu tính giới hạn của hàm số f(x) = (2x + 1) / (x - 3) khi x tiến tới vô cùng. Để giải bài tập này, các em có thể chia cả tử số và mẫu số cho x, sau đó tính giới hạn của biểu thức mới.
Trang 54 SGK Toán 12 tập 1 - Kết nối tri thức chứa các bài tập tổng hợp về giới hạn của hàm số tại một điểm và giới hạn vô cùng. Các bài tập này yêu cầu các em kết hợp các kiến thức và kỹ năng đã học để giải quyết các bài toán phức tạp hơn.
Ví dụ, bài tập 3 yêu cầu xét tính liên tục của hàm số f(x) = { x^2, nếu x ≤ 1; 2x - 1, nếu x > 1 } tại điểm x = 1. Để giải bài tập này, các em cần kiểm tra xem giới hạn của hàm số tại x = 1 có tồn tại và bằng giá trị của hàm số tại x = 1 hay không.
Hy vọng rằng với lời giải chi tiết và các lời khuyên trên, các em sẽ tự tin hơn khi giải các bài tập về giới hạn trong SGK Toán 12 tập 1 - Kết nối tri thức. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!