Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 tập 2 của giaitoan.edu.vn. Chúng tôi xin giới thiệu lời giải chi tiết và dễ hiểu cho mục 1 trang 29, 30, 31 sách giáo khoa Toán 12 tập 2 - Kết nối tri thức.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải bài tập và đạt kết quả tốt nhất trong môn Toán.
Vecto pháp tuyến và cặp vecto chỉ phương của mặt phẳng
Trả lời câu hỏi Luyện tập 1 trang 30 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, cho các điểm \(A\left( {1; - 2;3} \right),B\left( { - 3;0;1} \right)\). Gọi \(\left( \alpha \right)\) là mặt phẳng trung trực của đoạn thẳng AB. Hãy chỉ ra một vectơ pháp tuyến của \(\left( \alpha \right)\).
Phương pháp giải:
Sử dụng kiến thức về vectơ pháp tuyến của mặt phẳng để tính: Vectơ \(\overrightarrow n \ne \overrightarrow 0 \) được gọi là vectơ pháp tuyến của mặt phẳng \(\left( \alpha \right)\) nếu giá của \(\overrightarrow n \) vuông góc với \(\left( \alpha \right)\).
Lời giải chi tiết:
Vì \(\left( \alpha \right)\) là mặt phẳng trung trực của đoạn thẳng AB nên giá của \(\overrightarrow {AB} \bot \left( \alpha \right)\).
Do đó, một vectơ pháp tuyến của \(\left( \alpha \right)\) là \(\overrightarrow {AB} \left( { - 4;2; - 2} \right)\).
Trả lời câu hỏi Hoạt động 2 trang 30 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, cho hai vectơ \(\overrightarrow u = \left( {a,b,c} \right)\) và \(\overrightarrow v = \left( {a';b';c'} \right)\).
a) Vectơ \(\overrightarrow n = \left( {bc' - b'c;ca' - c'a;ab' - a'b} \right)\) có vuông góc với cả hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) hay không?
b) \(\overrightarrow n = \overrightarrow 0 \) khi và chỉ khi \(\overrightarrow u \) và \(\overrightarrow v \) có mối quan hệ gì?
Phương pháp giải:
Sử dụng kiến thức về tích vô hướng của 2 vectơ để chứng minh: Trong không gian Oxyz, tích vô hướng của 2 vectơ \(\overrightarrow a = \left( {x;y;z} \right)\) và \(\overrightarrow b = \left( {x';y';z'} \right)\) được xác định bởi công thức: \(\overrightarrow a .\overrightarrow b = xx' + yy' + zz'\).
Lời giải chi tiết:
a) Ta có: \(\overrightarrow n .\overrightarrow u = a\left( {bc' - b'c} \right) + b\left( {ca' - c'a} \right) + c\left( {ab' - a'b} \right)\)
\( = abc' - ab'c + cba' - abc' + ab'c - a'bc = \left( {abc' - abc'} \right) - \left( {ab'c - ab'c} \right) + \left( {cba' - cba'} \right) = 0\)
Do đó, vectơ \(\overrightarrow n \) vuông góc với vectơ \(\overrightarrow u \).
Ta có: \(\overrightarrow n .\overrightarrow v = a'\left( {bc' - b'c} \right) + b'\left( {ca' - c'a} \right) + c'\left( {ab' - a'b} \right)\)
\( = a'bc' - a'b'c + cb'a' - ab'c' + ab'c' - a'bc'\)
\( = \left( {a'bc' - a'bc'} \right) - \left( {a'b'c - a'b'c} \right) + \left( {ab'c' - ab'c'} \right) = 0\)
Do đó, vectơ \(\overrightarrow n \) vuông góc với vectơ \(\overrightarrow v \).
Suy ra, vectơ \(\overrightarrow n \) vuông góc với cả hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \).
b) Nếu \(\overrightarrow n = \overrightarrow 0 \) thì \(\left\{ \begin{array}{l}bc' - b'c = 0\\ca' - c'a = 0\\ab' - a'b = 0\end{array} \right.\left( I \right)\)
+ Với \(a = 0,b = 0,c = 0\) thì (I) luôn đúng. Khi đó, \(\overrightarrow u \) và \(\overrightarrow v \) cùng phương.
+ Với \(a \ne 0,b \ne 0,c \ne 0\), từ (I) ta có: \(\left\{ \begin{array}{l}\frac{{b'}}{b} = \frac{{c'}}{c}\\\frac{{a'}}{a} = \frac{{c'}}{c}\\\frac{{b'}}{b} = \frac{{a'}}{a}\end{array} \right.\), do đó, \(a' = ka,b' = kb,c' = kc\;\;\left( {k \in \mathbb{R}} \right)\)
Suy ra: \(\overrightarrow v = k\overrightarrow u \). Khi đó, \(\overrightarrow u \) và \(\overrightarrow v \) cùng phương.
Vậy \(\overrightarrow n = \overrightarrow 0 \) khi và chỉ khi \(\overrightarrow u \) và \(\overrightarrow v \) cùng phương.
Trả lời câu hỏi Luyện tập 2 trang 31 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, cho hai vectơ \(\overrightarrow u = \left( {2;3;1} \right)\) và \(\overrightarrow v = \left( {4;6;2} \right)\). Tính \(\left[ {\overrightarrow u ,\overrightarrow v } \right]\).
Phương pháp giải:
Sử dụng kiến thức về tích có hướng của hai vectơ để tính: Trong không gian Oxyz, cho hai vectơ \(\overrightarrow u = \left( {a;b;c} \right)\) và \(\overrightarrow v = \left( {a';b';c'} \right)\). Khi đó, vectơ \(\overrightarrow n = \left( {bc' - b'c;ca' - c'a;ab' - a'b} \right)\) vuông góc với cả hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \), được gọi là tích có hướng của \(\overrightarrow u \) và \(\overrightarrow v \), kí hiệu là \(\left[ {\overrightarrow u ,\overrightarrow v } \right]\).
Lời giải chi tiết:
Ta có: \(\left[ {\overrightarrow u ,\overrightarrow v } \right] = \left( {\left| \begin{array}{l}3\;\;1\\6\;\;2\end{array} \right|;\left| \begin{array}{l}1\;\;2\\2\;\;4\end{array} \right|;\left| \begin{array}{l}2\;\;3\\4\;\;6\end{array} \right|} \right) = \left( {0;0;0} \right)\)
Trả lời câu hỏi Hoạt động 3 trang 31 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, cho hai vectơ \(\overrightarrow u \), \(\overrightarrow v \) không cùng phương và có giá nằm trong hoặc song song với mặt phẳng (P).
a) Vectơ \(\left[ {\overrightarrow u ,\overrightarrow v } \right]\) có khác vectơ-không và giá của nó có vuông góc với cả hai giá của \(\overrightarrow u \), \(\overrightarrow v \) hay không?
b) Mặt phẳng (P) có nhận \(\left[ {\overrightarrow u ,\overrightarrow v } \right]\) làm một vectơ pháp tuyến hay không?
Phương pháp giải:
Sử dụng kiến thức về tích có hướng của hai vectơ để chứng minh: Trong không gian Oxyz, cho hai vectơ \(\overrightarrow u = \left( {a;b;c} \right)\) và \(\overrightarrow v = \left( {a';b';c'} \right)\). Khi đó, vectơ \(\overrightarrow n = \left( {bc' - b'c;ca' - c'a;ab' - a'b} \right)\) vuông góc với cả hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \), được gọi là tích có hướng của \(\overrightarrow u \) và \(\overrightarrow v \), kí hiệu là \(\left[ {\overrightarrow u ,\overrightarrow v } \right]\).
Sử dụng kiến thức về vectơ pháp tuyến của mặt phẳng để chứng minh: Vectơ \(\overrightarrow n \ne \overrightarrow 0 \) được gọi là vectơ pháp tuyến của mặt phẳng \(\left( \alpha \right)\) nếu giá của \(\overrightarrow n \) vuông góc với \(\left( \alpha \right)\).
Lời giải chi tiết:
a) Vectơ \(\left[ {\overrightarrow u ,\overrightarrow v } \right]\) có khác vectơ-không và giá của \(\left[ {\overrightarrow u ,\overrightarrow v } \right]\)vuông góc với cả hai giá của \(\overrightarrow u \), \(\overrightarrow v \) nếu hai vectơ \(\overrightarrow u \), \(\overrightarrow v \) không cùng phương.
b) Vì hai vectơ \(\overrightarrow u \), \(\overrightarrow v \) không cùng phương và có giá nằm trong hoặc song song với mặt phẳng (P), mà vectơ \(\left[ {\overrightarrow u ,\overrightarrow v } \right]\) có giá vuông góc với cả hai giá của \(\overrightarrow u \), \(\overrightarrow v \) nên giá của vectơ \(\left[ {\overrightarrow u ,\overrightarrow v } \right]\) vuông góc với mặt phẳng (P). Suy ra, mặt phẳng (P) nhận \(\left[ {\overrightarrow u ,\overrightarrow v } \right]\) làm một vectơ pháp tuyến.
Trả lời câu hỏi Luyện tập 3 trang 31 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, cho ba điểm không thẳng hàng \(A\left( {1; - 2;1} \right),B\left( { - 2;1;0} \right),C\left( { - 2;3;2} \right)\). Hãy chỉ ra một vectơ pháp tuyến của mặt phẳng (ABC).
Phương pháp giải:
Sử dụng kiến thức về vectơ pháp tuyến của mặt phẳng để tính: Trong không gian Oxyz, nếu \(\overrightarrow u \), \(\overrightarrow v \) là cặp vectơ chỉ phương của (P) thì \(\left[ {\overrightarrow u ,\overrightarrow v } \right]\) là một vectơ pháp tuyến của (P).
Lời giải chi tiết:
Ta có: \(\overrightarrow {AB} \left( { - 3;3; - 1} \right),\overrightarrow {AC} = \left( { - 3;5;1} \right)\). Vì \(\overrightarrow {AB} ,\overrightarrow {AC} \) là các vectơ chỉ phương của mặt phẳng (ABC) nên mặt phẳng (ABC) nhận \(\overrightarrow n = \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right]\) làm một vectơ pháp tuyến.
\(\overrightarrow n = \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = \left( {\left| \begin{array}{l}3\;\;\; - 1\\\;5\;\;\;\;\;1\end{array} \right|;\left| \begin{array}{l} - 1\;\; - 3\\\;\;1\;\; - 3\end{array} \right|;\left| \begin{array}{l} - 3\;\;3\\ - 3\;\;5\end{array} \right|} \right) = \left( {8;6; - 6} \right)\)
Trả lời câu hỏi Hoạt động 1 trang 29 SGK Toán 12 Kết nối tri thức
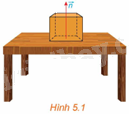
Trên mặt bàn phẳng, đặt một vật. Khi đó, mặt bàn tác động lên vật phản lực pháp tuyến \(\overrightarrow n \), giá của vectơ \(\overrightarrow n \) vuông góc với mặt bàn. Nếu mặt bàn thuộc mặt phẳng nằm ngang thì \(\overrightarrow n \) có phương gì? (H.5.1)
Phương pháp giải:
Sử dụng kiến thức về giá của vectơ để tìm phương của \(\overrightarrow n \): Đường thẳng đi qua điểm đầu và điểm cuối của một vectơ được gọi là giá của vectơ đó.
Lời giải chi tiết:
Nếu mặt bàn thuộc mặt phẳng nằm ngang thì \(\overrightarrow n \) có phương thẳng đứng, vuông góc với mặt bàn.
Trả lời câu hỏi Vận dụng 1 trang 31 SGK Toán 12 Kết nối tri thức
Moment lực là một đại lượng Vật lí, thể hiện tác động gây ra sự quay quanh một điểm hoặc một trục của một vật thể. Trong không gian Oxyz, với đơn vị đo là mét, nếu tác động vào cán mỏ lết tại vị trí P một lực \(\overrightarrow F \) để vặn con ốc ở vị trí O (H.5.6) thì moment lực \(\overrightarrow M \) được tính bởi công thức \(\overrightarrow M = \left[ {\overrightarrow {OP} ,\overrightarrow F } \right]\).
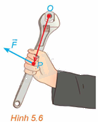
a) Cho \(\overrightarrow {OP} = \left( {x;y;z} \right),\overrightarrow F = \left( {a;b;c} \right)\), Tính \(\overrightarrow M \).
b) Giải thích vì sao, nếu giữ nguyên lực tác động \(\overrightarrow F \) trong khi thay vị trí đặt lực từ P sang P’ sao cho \(\overrightarrow {OP'} = 2\overrightarrow {OP} \) thì moment lực sẽ tăng lên gấp đôi. Từ đó, ta có thể rút ra điều gì để đỡ tốn sức khi dùng mỏ lết vặn ốc?
Phương pháp giải:
Sử dụng kiến thức về tích có hướng của hai vectơ để tính: Trong không gian Oxyz, cho hai vectơ \(\overrightarrow u = \left( {a;b;c} \right)\) và \(\overrightarrow v = \left( {a';b';c'} \right)\). Khi đó, vectơ \(\overrightarrow n = \left( {bc' - b'c;ca' - c'a;ab' - a'b} \right)\) vuông góc với cả hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \), được gọi là tích có hướng của \(\overrightarrow u \) và \(\overrightarrow v \), kí hiệu là \(\left[ {\overrightarrow u ,\overrightarrow v } \right]\).
Lời giải chi tiết:
a) Ta có: \(\left[ {\overrightarrow {OP} ,\overrightarrow F } \right] = \left( {\left| {\begin{array}{*{20}{c}}y&z\\b&c\end{array}} \right|;\left| {\begin{array}{*{20}{c}}z&x\\c&a\end{array}} \right|;\left| {\begin{array}{*{20}{c}}x&y\\a&b\end{array}} \right|} \right) = \left( {cy - bz;za - cx;xb - ay} \right)\)
Do đó, \(\overrightarrow M = \left( {cy - bz;za - cx;xb - ay} \right)\).
b) Ta có: \(\overrightarrow {OP'} = \left( {2x;2y;2z} \right)\). Khi đó, moment lực là: \(\overrightarrow {M'} = \left[ {\overrightarrow {OP'} ,\overrightarrow F } \right]\)
Do đó, \(\left[ {\overrightarrow {OP'} ,\overrightarrow F } \right] = \left( {\left| {\begin{array}{*{20}{c}}{2y}&{2z}\\b&c\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{2z}&{2x}\\c&a\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{2x}&{2y}\\a&b\end{array}} \right|} \right) = \left( {2cy - 2bz;2za - 2cx;2xb - 2ay} \right)\)
Suy ra: \(\overrightarrow {M'} = \left( {2cy - 2bz;2za - 2cx;2xb - 2ay} \right) = 2\overrightarrow M \)
Vậy khi giữ nguyên lực tác động \(\overrightarrow F \) trong khi thay vị trí đặt lực từ P sang P’ sao cho \(\overrightarrow {OP'} = 2\overrightarrow {OP} \) thì moment lực sẽ tăng lên gấp đôi.
Từ đó, ta rút ra kết luận là nếu tác động vào cán mỏ lết tại vị trí P cách con ốc ở vị trí O càng lớn thì càng đỡ tốn sức khi dùng mỏ lết vặn ốc.
Trả lời câu hỏi Hoạt động 1 trang 29 SGK Toán 12 Kết nối tri thức
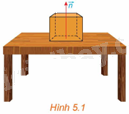
Trên mặt bàn phẳng, đặt một vật. Khi đó, mặt bàn tác động lên vật phản lực pháp tuyến \(\overrightarrow n \), giá của vectơ \(\overrightarrow n \) vuông góc với mặt bàn. Nếu mặt bàn thuộc mặt phẳng nằm ngang thì \(\overrightarrow n \) có phương gì? (H.5.1)
Phương pháp giải:
Sử dụng kiến thức về giá của vectơ để tìm phương của \(\overrightarrow n \): Đường thẳng đi qua điểm đầu và điểm cuối của một vectơ được gọi là giá của vectơ đó.
Lời giải chi tiết:
Nếu mặt bàn thuộc mặt phẳng nằm ngang thì \(\overrightarrow n \) có phương thẳng đứng, vuông góc với mặt bàn.
Trả lời câu hỏi Luyện tập 1 trang 30 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, cho các điểm \(A\left( {1; - 2;3} \right),B\left( { - 3;0;1} \right)\). Gọi \(\left( \alpha \right)\) là mặt phẳng trung trực của đoạn thẳng AB. Hãy chỉ ra một vectơ pháp tuyến của \(\left( \alpha \right)\).
Phương pháp giải:
Sử dụng kiến thức về vectơ pháp tuyến của mặt phẳng để tính: Vectơ \(\overrightarrow n \ne \overrightarrow 0 \) được gọi là vectơ pháp tuyến của mặt phẳng \(\left( \alpha \right)\) nếu giá của \(\overrightarrow n \) vuông góc với \(\left( \alpha \right)\).
Lời giải chi tiết:
Vì \(\left( \alpha \right)\) là mặt phẳng trung trực của đoạn thẳng AB nên giá của \(\overrightarrow {AB} \bot \left( \alpha \right)\).
Do đó, một vectơ pháp tuyến của \(\left( \alpha \right)\) là \(\overrightarrow {AB} \left( { - 4;2; - 2} \right)\).
Trả lời câu hỏi Hoạt động 2 trang 30 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, cho hai vectơ \(\overrightarrow u = \left( {a,b,c} \right)\) và \(\overrightarrow v = \left( {a';b';c'} \right)\).
a) Vectơ \(\overrightarrow n = \left( {bc' - b'c;ca' - c'a;ab' - a'b} \right)\) có vuông góc với cả hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) hay không?
b) \(\overrightarrow n = \overrightarrow 0 \) khi và chỉ khi \(\overrightarrow u \) và \(\overrightarrow v \) có mối quan hệ gì?
Phương pháp giải:
Sử dụng kiến thức về tích vô hướng của 2 vectơ để chứng minh: Trong không gian Oxyz, tích vô hướng của 2 vectơ \(\overrightarrow a = \left( {x;y;z} \right)\) và \(\overrightarrow b = \left( {x';y';z'} \right)\) được xác định bởi công thức: \(\overrightarrow a .\overrightarrow b = xx' + yy' + zz'\).
Lời giải chi tiết:
a) Ta có: \(\overrightarrow n .\overrightarrow u = a\left( {bc' - b'c} \right) + b\left( {ca' - c'a} \right) + c\left( {ab' - a'b} \right)\)
\( = abc' - ab'c + cba' - abc' + ab'c - a'bc = \left( {abc' - abc'} \right) - \left( {ab'c - ab'c} \right) + \left( {cba' - cba'} \right) = 0\)
Do đó, vectơ \(\overrightarrow n \) vuông góc với vectơ \(\overrightarrow u \).
Ta có: \(\overrightarrow n .\overrightarrow v = a'\left( {bc' - b'c} \right) + b'\left( {ca' - c'a} \right) + c'\left( {ab' - a'b} \right)\)
\( = a'bc' - a'b'c + cb'a' - ab'c' + ab'c' - a'bc'\)
\( = \left( {a'bc' - a'bc'} \right) - \left( {a'b'c - a'b'c} \right) + \left( {ab'c' - ab'c'} \right) = 0\)
Do đó, vectơ \(\overrightarrow n \) vuông góc với vectơ \(\overrightarrow v \).
Suy ra, vectơ \(\overrightarrow n \) vuông góc với cả hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \).
b) Nếu \(\overrightarrow n = \overrightarrow 0 \) thì \(\left\{ \begin{array}{l}bc' - b'c = 0\\ca' - c'a = 0\\ab' - a'b = 0\end{array} \right.\left( I \right)\)
+ Với \(a = 0,b = 0,c = 0\) thì (I) luôn đúng. Khi đó, \(\overrightarrow u \) và \(\overrightarrow v \) cùng phương.
+ Với \(a \ne 0,b \ne 0,c \ne 0\), từ (I) ta có: \(\left\{ \begin{array}{l}\frac{{b'}}{b} = \frac{{c'}}{c}\\\frac{{a'}}{a} = \frac{{c'}}{c}\\\frac{{b'}}{b} = \frac{{a'}}{a}\end{array} \right.\), do đó, \(a' = ka,b' = kb,c' = kc\;\;\left( {k \in \mathbb{R}} \right)\)
Suy ra: \(\overrightarrow v = k\overrightarrow u \). Khi đó, \(\overrightarrow u \) và \(\overrightarrow v \) cùng phương.
Vậy \(\overrightarrow n = \overrightarrow 0 \) khi và chỉ khi \(\overrightarrow u \) và \(\overrightarrow v \) cùng phương.
Trả lời câu hỏi Luyện tập 2 trang 31 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, cho hai vectơ \(\overrightarrow u = \left( {2;3;1} \right)\) và \(\overrightarrow v = \left( {4;6;2} \right)\). Tính \(\left[ {\overrightarrow u ,\overrightarrow v } \right]\).
Phương pháp giải:
Sử dụng kiến thức về tích có hướng của hai vectơ để tính: Trong không gian Oxyz, cho hai vectơ \(\overrightarrow u = \left( {a;b;c} \right)\) và \(\overrightarrow v = \left( {a';b';c'} \right)\). Khi đó, vectơ \(\overrightarrow n = \left( {bc' - b'c;ca' - c'a;ab' - a'b} \right)\) vuông góc với cả hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \), được gọi là tích có hướng của \(\overrightarrow u \) và \(\overrightarrow v \), kí hiệu là \(\left[ {\overrightarrow u ,\overrightarrow v } \right]\).
Lời giải chi tiết:
Ta có: \(\left[ {\overrightarrow u ,\overrightarrow v } \right] = \left( {\left| \begin{array}{l}3\;\;1\\6\;\;2\end{array} \right|;\left| \begin{array}{l}1\;\;2\\2\;\;4\end{array} \right|;\left| \begin{array}{l}2\;\;3\\4\;\;6\end{array} \right|} \right) = \left( {0;0;0} \right)\)
Trả lời câu hỏi Hoạt động 3 trang 31 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, cho hai vectơ \(\overrightarrow u \), \(\overrightarrow v \) không cùng phương và có giá nằm trong hoặc song song với mặt phẳng (P).
a) Vectơ \(\left[ {\overrightarrow u ,\overrightarrow v } \right]\) có khác vectơ-không và giá của nó có vuông góc với cả hai giá của \(\overrightarrow u \), \(\overrightarrow v \) hay không?
b) Mặt phẳng (P) có nhận \(\left[ {\overrightarrow u ,\overrightarrow v } \right]\) làm một vectơ pháp tuyến hay không?
Phương pháp giải:
Sử dụng kiến thức về tích có hướng của hai vectơ để chứng minh: Trong không gian Oxyz, cho hai vectơ \(\overrightarrow u = \left( {a;b;c} \right)\) và \(\overrightarrow v = \left( {a';b';c'} \right)\). Khi đó, vectơ \(\overrightarrow n = \left( {bc' - b'c;ca' - c'a;ab' - a'b} \right)\) vuông góc với cả hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \), được gọi là tích có hướng của \(\overrightarrow u \) và \(\overrightarrow v \), kí hiệu là \(\left[ {\overrightarrow u ,\overrightarrow v } \right]\).
Sử dụng kiến thức về vectơ pháp tuyến của mặt phẳng để chứng minh: Vectơ \(\overrightarrow n \ne \overrightarrow 0 \) được gọi là vectơ pháp tuyến của mặt phẳng \(\left( \alpha \right)\) nếu giá của \(\overrightarrow n \) vuông góc với \(\left( \alpha \right)\).
Lời giải chi tiết:
a) Vectơ \(\left[ {\overrightarrow u ,\overrightarrow v } \right]\) có khác vectơ-không và giá của \(\left[ {\overrightarrow u ,\overrightarrow v } \right]\)vuông góc với cả hai giá của \(\overrightarrow u \), \(\overrightarrow v \) nếu hai vectơ \(\overrightarrow u \), \(\overrightarrow v \) không cùng phương.
b) Vì hai vectơ \(\overrightarrow u \), \(\overrightarrow v \) không cùng phương và có giá nằm trong hoặc song song với mặt phẳng (P), mà vectơ \(\left[ {\overrightarrow u ,\overrightarrow v } \right]\) có giá vuông góc với cả hai giá của \(\overrightarrow u \), \(\overrightarrow v \) nên giá của vectơ \(\left[ {\overrightarrow u ,\overrightarrow v } \right]\) vuông góc với mặt phẳng (P). Suy ra, mặt phẳng (P) nhận \(\left[ {\overrightarrow u ,\overrightarrow v } \right]\) làm một vectơ pháp tuyến.
Trả lời câu hỏi Luyện tập 3 trang 31 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, cho ba điểm không thẳng hàng \(A\left( {1; - 2;1} \right),B\left( { - 2;1;0} \right),C\left( { - 2;3;2} \right)\). Hãy chỉ ra một vectơ pháp tuyến của mặt phẳng (ABC).
Phương pháp giải:
Sử dụng kiến thức về vectơ pháp tuyến của mặt phẳng để tính: Trong không gian Oxyz, nếu \(\overrightarrow u \), \(\overrightarrow v \) là cặp vectơ chỉ phương của (P) thì \(\left[ {\overrightarrow u ,\overrightarrow v } \right]\) là một vectơ pháp tuyến của (P).
Lời giải chi tiết:
Ta có: \(\overrightarrow {AB} \left( { - 3;3; - 1} \right),\overrightarrow {AC} = \left( { - 3;5;1} \right)\). Vì \(\overrightarrow {AB} ,\overrightarrow {AC} \) là các vectơ chỉ phương của mặt phẳng (ABC) nên mặt phẳng (ABC) nhận \(\overrightarrow n = \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right]\) làm một vectơ pháp tuyến.
\(\overrightarrow n = \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = \left( {\left| \begin{array}{l}3\;\;\; - 1\\\;5\;\;\;\;\;1\end{array} \right|;\left| \begin{array}{l} - 1\;\; - 3\\\;\;1\;\; - 3\end{array} \right|;\left| \begin{array}{l} - 3\;\;3\\ - 3\;\;5\end{array} \right|} \right) = \left( {8;6; - 6} \right)\)
Trả lời câu hỏi Vận dụng 1 trang 31 SGK Toán 12 Kết nối tri thức
Moment lực là một đại lượng Vật lí, thể hiện tác động gây ra sự quay quanh một điểm hoặc một trục của một vật thể. Trong không gian Oxyz, với đơn vị đo là mét, nếu tác động vào cán mỏ lết tại vị trí P một lực \(\overrightarrow F \) để vặn con ốc ở vị trí O (H.5.6) thì moment lực \(\overrightarrow M \) được tính bởi công thức \(\overrightarrow M = \left[ {\overrightarrow {OP} ,\overrightarrow F } \right]\).
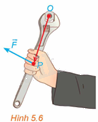
a) Cho \(\overrightarrow {OP} = \left( {x;y;z} \right),\overrightarrow F = \left( {a;b;c} \right)\), Tính \(\overrightarrow M \).
b) Giải thích vì sao, nếu giữ nguyên lực tác động \(\overrightarrow F \) trong khi thay vị trí đặt lực từ P sang P’ sao cho \(\overrightarrow {OP'} = 2\overrightarrow {OP} \) thì moment lực sẽ tăng lên gấp đôi. Từ đó, ta có thể rút ra điều gì để đỡ tốn sức khi dùng mỏ lết vặn ốc?
Phương pháp giải:
Sử dụng kiến thức về tích có hướng của hai vectơ để tính: Trong không gian Oxyz, cho hai vectơ \(\overrightarrow u = \left( {a;b;c} \right)\) và \(\overrightarrow v = \left( {a';b';c'} \right)\). Khi đó, vectơ \(\overrightarrow n = \left( {bc' - b'c;ca' - c'a;ab' - a'b} \right)\) vuông góc với cả hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \), được gọi là tích có hướng của \(\overrightarrow u \) và \(\overrightarrow v \), kí hiệu là \(\left[ {\overrightarrow u ,\overrightarrow v } \right]\).
Lời giải chi tiết:
a) Ta có: \(\left[ {\overrightarrow {OP} ,\overrightarrow F } \right] = \left( {\left| {\begin{array}{*{20}{c}}y&z\\b&c\end{array}} \right|;\left| {\begin{array}{*{20}{c}}z&x\\c&a\end{array}} \right|;\left| {\begin{array}{*{20}{c}}x&y\\a&b\end{array}} \right|} \right) = \left( {cy - bz;za - cx;xb - ay} \right)\)
Do đó, \(\overrightarrow M = \left( {cy - bz;za - cx;xb - ay} \right)\).
b) Ta có: \(\overrightarrow {OP'} = \left( {2x;2y;2z} \right)\). Khi đó, moment lực là: \(\overrightarrow {M'} = \left[ {\overrightarrow {OP'} ,\overrightarrow F } \right]\)
Do đó, \(\left[ {\overrightarrow {OP'} ,\overrightarrow F } \right] = \left( {\left| {\begin{array}{*{20}{c}}{2y}&{2z}\\b&c\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{2z}&{2x}\\c&a\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{2x}&{2y}\\a&b\end{array}} \right|} \right) = \left( {2cy - 2bz;2za - 2cx;2xb - 2ay} \right)\)
Suy ra: \(\overrightarrow {M'} = \left( {2cy - 2bz;2za - 2cx;2xb - 2ay} \right) = 2\overrightarrow M \)
Vậy khi giữ nguyên lực tác động \(\overrightarrow F \) trong khi thay vị trí đặt lực từ P sang P’ sao cho \(\overrightarrow {OP'} = 2\overrightarrow {OP} \) thì moment lực sẽ tăng lên gấp đôi.
Từ đó, ta rút ra kết luận là nếu tác động vào cán mỏ lết tại vị trí P cách con ốc ở vị trí O càng lớn thì càng đỡ tốn sức khi dùng mỏ lết vặn ốc.
Mục 1 của chương trình Toán 12 tập 2 - Kết nối tri thức thường tập trung vào các kiến thức về đạo hàm của hàm số. Việc nắm vững các khái niệm và công thức đạo hàm là nền tảng quan trọng để giải quyết các bài toán liên quan đến cực trị, đơn điệu và ứng dụng của đạo hàm trong các lĩnh vực khác.
Dưới đây là giải chi tiết từng bài tập trong mục 1 trang 29, 30, 31 SGK Toán 12 tập 2 - Kết nối tri thức:
Lời giải:
y = (x2 + 1) / (x - 2)
Lời giải:
Sử dụng quy tắc đạo hàm của thương:
y' = [(x2 + 1)'(x - 2) - (x2 + 1)(x - 2)'] / (x - 2)2
y' = [2x(x - 2) - (x2 + 1)] / (x - 2)2
y' = (x2 - 4x - 1) / (x - 2)2
Lời giải:
f'(x) = 4x3 - 8x
f''(x) = 12x2 - 8
Đạo hàm có rất nhiều ứng dụng trong thực tế, bao gồm:
Hy vọng với lời giải chi tiết và những kiến thức bổ ích trên, các em sẽ hiểu rõ hơn về cách giải bài tập mục 1 trang 29,30,31 SGK Toán 12 tập 2 - Kết nối tri thức. Chúc các em học tập tốt!