Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 12. Bài viết này sẽ hướng dẫn bạn cách giải bài tập 5.10 trang 40 SGK Toán 12 tập 2 - Kết nối tri thức một cách nhanh chóng và hiệu quả.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp bạn nắm vững kiến thức và đạt kết quả cao trong môn Toán.
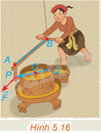
Xét một cối xay lúa trong không gian Oxyz, với đơn vị đo là mét. Nếu tác động vào tai cối xay lúa (ở vị trí P) một lực \(\overrightarrow F \) thì moment lực \(\overrightarrow M \) được tính bởi công thức \(\overrightarrow M = \left[ {\overrightarrow {OP} ,\overrightarrow F } \right]\) (H.5.16). Trong quá trình xay, các thanh gỗ AB và PQ luôn có phương nằm ngang. Vectơ lực \(\overrightarrow F \) có giá song song với AB. Giải thích vì sao giá của vectơ moment lực \(\overrightarrow F \) có phương
Đề bài
Xét một cối xay lúa trong không gian Oxyz, với đơn vị đo là mét. Nếu tác động vào tai cối xay lúa (ở vị trí P) một lực \(\overrightarrow F \) thì moment lực \(\overrightarrow M \) được tính bởi công thức \(\overrightarrow M = \left[ {\overrightarrow {OP} ,\overrightarrow F } \right]\) (H.5.16). Trong quá trình xay, các thanh gỗ AB và PQ luôn có phương nằm ngang. Vectơ lực \(\overrightarrow F \) có giá song song với AB. Giải thích vì sao giá của vectơ moment lực \(\overrightarrow F \) có phương thẳng đứng?
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về tích có hướng của hai vectơ để tính: Trong không gian Oxyz, cho hai vectơ \(\overrightarrow u = \left( {a;b;c} \right)\) và \(\overrightarrow v = \left( {a';b';c'} \right)\). Khi đó, vectơ \(\overrightarrow n = \left( {bc' - b'c;ca' - c'a;ab' - a'b} \right)\) vuông góc với hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \), được gọi là tích có hướng của \(\overrightarrow u \) và \(\overrightarrow v \), kí hiệu là \(\left[ {\overrightarrow u ,\overrightarrow v } \right]\)
Lời giải chi tiết
Vì các thanh gỗ AB và PQ luôn có phương nằm ngang và vectơ lực \(\overrightarrow F \) có giá song song với AB nên giá của các vectơ \(\overrightarrow {OP} ,\overrightarrow F \) có phương nằm ngang.
Vì moment lực \(\overrightarrow M \) được tính bởi công thức \(\overrightarrow M = \left[ {\overrightarrow {OP} ,\overrightarrow F } \right]\) nên moment lực \(\overrightarrow M \) vuông góc với hai vectơ \(\overrightarrow {OP} ,\overrightarrow F \).
Do đó, giá của vectơ moment lực \(\overrightarrow F \) có phương thẳng đứng.
Bài tập 5.10 trang 40 SGK Toán 12 tập 2 - Kết nối tri thức thuộc chương trình học về đạo hàm của hàm số. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế, cụ thể là tìm đạo hàm của hàm số và sử dụng đạo hàm để khảo sát hàm số.
Bài tập 5.10 thường bao gồm các dạng câu hỏi sau:
Để giải bài tập 5.10 một cách hiệu quả, bạn cần nắm vững các kiến thức sau:
Dưới đây là lời giải chi tiết cho bài tập 5.10 trang 40 SGK Toán 12 tập 2 - Kết nối tri thức. (Lưu ý: Nội dung lời giải chi tiết sẽ được trình bày cụ thể dựa trên nội dung bài tập thực tế. Ví dụ này chỉ mang tính chất minh họa.)
Ví dụ: Giả sử bài tập yêu cầu tính đạo hàm của hàm số f(x) = x3 - 3x2 + 2x - 1.
Lời giải:
f'(x) = 3x2 - 6x + 2
Ngoài bài tập 5.10, còn rất nhiều bài tập tương tự trong SGK Toán 12 tập 2 - Kết nối tri thức. Để giải các bài tập này, bạn có thể áp dụng các phương pháp tương tự như đã trình bày ở trên. Quan trọng là bạn cần hiểu rõ bản chất của bài toán và vận dụng kiến thức một cách linh hoạt.
Bài tập 5.10 trang 40 SGK Toán 12 tập 2 - Kết nối tri thức là một bài tập quan trọng giúp bạn củng cố kiến thức về đạo hàm và ứng dụng của đạo hàm. Hy vọng với lời giải chi tiết và các phương pháp giải bài tập được trình bày ở trên, bạn sẽ tự tin hơn trong việc giải quyết các bài toán tương tự.
| Hàm số | Đạo hàm |
|---|---|
| f(x) = c (hằng số) | f'(x) = 0 |
| f(x) = xn | f'(x) = nxn-1 |
| f(x) = sin(x) | f'(x) = cos(x) |
| f(x) = cos(x) | f'(x) = -sin(x) |