Bài tập 1.39 trang 43 SGK Toán 12 tập 1 thuộc chương trình học Toán 12 Kết nối tri thức. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm của hàm số để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập 1.39, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
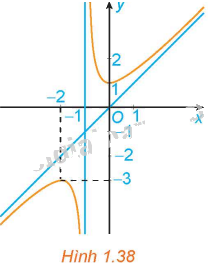
Đồ thị trong Hình 1.38 là đồ thị của hàm số: A. \(y = x - \frac{1}{{x + 1}}\). B. \(y = \frac{{2x + 1}}{{x + 1}}\). C. \(y = \frac{{{x^2} - x + 1}}{{x + 1}}\). D. \(y = \frac{{{x^2} + x + 1}}{{x + 1}}\).
Đề bài
Đồ thị trong Hình 1.38 là đồ thị của hàm số:
A. \(y = x - \frac{1}{{x + 1}}\).B. \(y = \frac{{2x + 1}}{{x + 1}}\).C. \(y = \frac{{{x^2} - x + 1}}{{x + 1}}\).D. \(y = \frac{{{x^2} + x + 1}}{{x + 1}}\).
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về điểm thuộc đồ thị hàm số, dạng của đồ thị hàm số, tiệm cận của đồ thị hàm số để tìm đồ thị hàm số đúng.
Lời giải chi tiết
Đồ thị hàm số trong hình 1.38 có dạng: \(y = \frac{{a{x^2} + bx + c}}{{px + q}}\left( {a \ne 0,p \ne 0} \right)\) và đa thức tử không chia hết cho đa thức mẫu. Do đó, loại đáp án B.
Đồ thị hàm số trong hình 1.38 đi qua điểm \[\left( { - 2; - 3} \right)\]. Do đó, loại đáp án C.
Đồ thị hàm số trong hình 1.38 đi qua điểm (0; 1). Do đó, loại đáp án A.
Hàm số \(y = \frac{{{x^2} + x + 1}}{{x + 1}} = x + \frac{1}{{x + 1}}\) có:
+ \(\mathop {\lim }\limits_{x \to - {1^ + }} \frac{{{x^2} + x + 1}}{{x + 1}} = + \infty ;\mathop {\lim }\limits_{x \to - {1^ - }} \frac{{{x^2} + x + 1}}{{x + 1}} = - \infty \) nên đường thẳng \(x = - 1\) là tiệm cận đứng của đồ thị hàm số.
+ \(\mathop {\lim }\limits_{x \to + \infty } \left( {y - x} \right) = \mathop {\lim }\limits_{x \to + \infty } \left[ {x + \frac{1}{{x + 1}} - x} \right] = \mathop {\lim }\limits_{x \to + \infty } \frac{1}{{x + 1}} = 0\), \(\mathop {\lim }\limits_{x \to - \infty } \left( {y - x} \right) = \mathop {\lim }\limits_{x \to - \infty } \left[ {x + \frac{1}{{x + 1}} - x} \right] = \mathop {\lim }\limits_{x \to - \infty } \frac{1}{{x + 1}} = 0\) nên đường thẳng \(y = x\) là tiệm cận xiên của đồ thị hàm số.
Chọn D
Bài tập 1.39 SGK Toán 12 tập 1 Kết nối tri thức là một bài toán ứng dụng đạo hàm để giải quyết một vấn đề thực tế. Để giải bài tập này, học sinh cần nắm vững các kiến thức sau:
Bài tập 1.39 thường yêu cầu học sinh tìm giá trị lớn nhất hoặc nhỏ nhất của một hàm số trong một khoảng cho trước, hoặc tìm điều kiện để một hàm số có cực trị. Để giải bài tập này, học sinh cần thực hiện các bước sau:
Giả sử bài tập 1.39 yêu cầu tìm giá trị lớn nhất của hàm số f(x) = -x2 + 4x + 1 trên đoạn [-1; 3].
Bước 1: Tính đạo hàm của hàm số:
f'(x) = -2x + 4
Bước 2: Tìm các điểm cực trị của hàm số:
-2x + 4 = 0 => x = 2
Bước 3: Xác định loại cực trị:
f''(x) = -2 < 0 => x = 2 là điểm cực đại.
Bước 4: Tính giá trị của hàm số tại các điểm cực trị và các điểm đầu mút của khoảng:
f(-1) = -(-1)2 + 4(-1) + 1 = -4
f(2) = -(2)2 + 4(2) + 1 = 5
f(3) = -(3)2 + 4(3) + 1 = 4
Bước 5: So sánh các giá trị:
Giá trị lớn nhất của hàm số trên đoạn [-1; 3] là 5, đạt được tại x = 2.
Khi giải bài tập 1.39, học sinh cần chú ý các điểm sau:
Giaitoan.edu.vn là website học toán online uy tín, cung cấp lời giải chi tiết, dễ hiểu cho các bài tập Toán từ lớp 6 đến lớp 12. Chúng tôi luôn cập nhật kiến thức mới nhất và phương pháp giải bài tập hiệu quả, giúp bạn học Toán một cách dễ dàng và thú vị.
| Hàm số | Đạo hàm |
|---|---|
| y = c (c là hằng số) | y' = 0 |
| y = xn | y' = nxn-1 |
| y = sinx | y' = cosx |
| y = cosx | y' = -sinx |
