Bài tập 6.18 trang 79 SGK Toán 12 tập 2 thuộc chương trình học Toán 12 Kết nối tri thức. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế liên quan đến tối ưu hóa.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập 6.18, giúp các em học sinh hiểu rõ phương pháp giải và áp dụng vào các bài tập tương tự.
Để thử nghiệm tác dụng điều trị bệnh mất ngủ của hai loại thuốc X và thuốc Y, người ta tiến hành thử nghiệm với 4 000 người bệnh tình nguyện. Kết quả được cho trong bảng dữ liệu thống kê \(2 \times 2\) sau: Chọn ngẫu nhiên một người bệnh tham gia tình nguyện thử nghiệm thuốc. a) Tính xác suất để người đó khỏi bệnh nếu biết người đó uống thuốc X. b) Tính xác suất để người bệnh đó uống thuốc Y, biết rằng người đó khỏi bệnh.
Đề bài
Để thử nghiệm tác dụng điều trị bệnh mất ngủ của hai loại thuốc X và thuốc Y, người ta tiến hành thử nghiệm với 4 000 người bệnh tình nguyện. Kết quả được cho trong bảng dữ liệu thống kê \(2 \times 2\) sau:
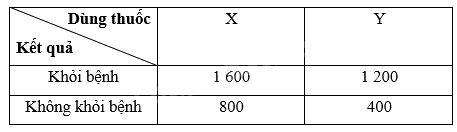
Chọn ngẫu nhiên một người bệnh tham gia tình nguyện thử nghiệm thuốc.
a) Tính xác suất để người đó khỏi bệnh nếu biết người đó uống thuốc X.
b) Tính xác suất để người bệnh đó uống thuốc Y, biết rằng người đó khỏi bệnh.
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về công thức tính xác suất có điều kiện để tính: Cho hai biến cố A và B bất kì, với \(P\left( B \right) > 0\). Khi đó, \(P\left( {A|B} \right) = \frac{{P\left( {AB} \right)}}{{P\left( B \right)}}\)
Lời giải chi tiết
Không gian mẫu \(\Omega \) là tập hợp gồm 4 000 bệnh nhân thử nghiệm nên \(n\left( \Omega \right) = 4000\)
a) Gọi A là biến cố: “Người đó uống thuốc X”, B là biến cố “Người đó khỏi bệnh”.
Khi đó biến cố AB là: “Người đó uống thuốc X và khỏi bệnh”
Ta có: \(1600 + 800 = 2400\) người uống thuốc X nên \(n\left( A \right) = 2400\). Do đó, \(P\left( A \right) = \frac{{2400}}{{4000}}\)
Trong số những người uống thuốc X, có 1 600 người khỏi bệnh nên \(n\left( {AB} \right) = 1\;600\)
Do đó, \(P\left( {AB} \right) = \frac{{1600}}{{4000}}\). Vậy \(P\left( {B|A} \right) = \frac{{P\left( {AB} \right)}}{{P\left( A \right)}} = \frac{{1600}}{{2400}} = \frac{2}{3}\)
b) Gọi A là biến cố: “Người đó uống thuốc Y”, B là biến cố “Người đó khỏi bệnh”
Khi đó biến cố AB là: “Người đó uống thuốc Y và khỏi bệnh”.
Ta có: \(1200 + 1600 = 2800\) khỏi bệnh nên \(n\left( B \right) = 2800\). Do đó, \(P\left( B \right) = \frac{{2800}}{{4000}}\)
Trong số những người khỏi bệnh, có 1200 người uống thuốc Y nên \(n\left( {AB} \right) = 1200\)
Do đó, \(P\left( {AB} \right) = \frac{{1200}}{{2800}}\). Vậy \(P\left( {A|B} \right) = \frac{{P\left( {AB} \right)}}{{P\left( B \right)}} = \frac{{1200}}{{2800}} = \frac{3}{7}\)
Bài tập 6.18 SGK Toán 12 tập 2 Kết nối tri thức yêu cầu học sinh giải quyết một bài toán tối ưu hóa, thường liên quan đến việc tìm giá trị lớn nhất hoặc nhỏ nhất của một hàm số trong một khoảng cho trước. Đề bài cụ thể sẽ cung cấp thông tin về hàm số, khoảng xác định và yêu cầu tìm giá trị tối ưu.
Để giải bài toán tối ưu hóa, chúng ta thường thực hiện các bước sau:
(Nội dung lời giải chi tiết bài tập 6.18 sẽ được trình bày tại đây. Bao gồm các bước giải cụ thể, các phép tính và giải thích rõ ràng. Ví dụ:)
Ví dụ: Giả sử đề bài yêu cầu tìm giá trị nhỏ nhất của hàm số f(x) = x2 - 4x + 5 trên khoảng [0, 3].
Bài toán tối ưu hóa có rất nhiều ứng dụng trong thực tế, như:
Để củng cố kiến thức về bài toán tối ưu hóa, bạn có thể tham khảo các bài tập tương tự sau:
Bài tập 6.18 trang 79 SGK Toán 12 tập 2 - Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải bài toán tối ưu hóa. Việc nắm vững phương pháp giải và các lưu ý khi giải bài toán sẽ giúp các em học sinh tự tin giải quyết các bài tập tương tự và ứng dụng kiến thức vào thực tế.