Bài tập 1.44 trang 44 SGK Toán 12 tập 1 thuộc chương trình học Toán 12 Kết nối tri thức. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm của hàm số để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập 1.44, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Xét một thấu kính hội tụ có tiêu cự f (H.1.39). Khoảng cách p từ vật đến thấu kính liên hệ với khoảng cách q từ ảnh đến thấu kính bởi hệ thức: \(\frac{1}{p} + \frac{1}{q} = \frac{1}{f}\). a) Viết công thức tính \(q = g\left( p \right)\) như một hàm số của biến \(p \in \left( {f; + \infty } \right)\). b) Tính các giới hạn \(\mathop {\lim }\limits_{p \to + \infty } g\left( p \right),\mathop {\lim }\limits_{p \to {f^ + }} g\left( p \right)\) và giải thích ý nghĩa các kết quả này. Lập bảng bi
Đề bài
Xét một thấu kính hội tụ có tiêu cự f (H.1.39). Khoảng cách p từ vật đến thấu kính liên hệ với khoảng cách q từ ảnh đến thấu kính bởi hệ thức: \(\frac{1}{p} + \frac{1}{q} = \frac{1}{f}\).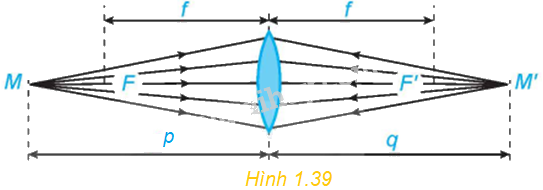 
a) Viết công thức tính \(q = g\left( p \right)\) như một hàm số của biến \(p \in \left( {f; + \infty } \right)\).b) Tính các giới hạn \(\mathop {\lim }\limits_{p \to + \infty } g\left( p \right),\mathop {\lim }\limits_{p \to {f^ + }} g\left( p \right)\) và giải thích ý nghĩa các kết quả này.Lập bảng biến thiên của hàm số \(q = g\left( p \right)\) trên khoảng \(\left( {f; + \infty } \right)\).
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về tính giới hạn của hàm số để tính.
Sử dụng kiến thức về lập bảng biến thiên của hàm số để lập bảng biến thiên: Lập bảng biến thiên của hàm số, tức là lập bảng thể hiện dấu của đạo hàm và sự đồng biến, nghịch biến của hàm số trên các khoảng tương ứng.
Lời giải chi tiết
a) Ta có: \(\frac{1}{p} + \frac{1}{q} = \frac{1}{f} \Rightarrow q = \frac{{pf}}{{p - f}}\). Do đó, \(q = g\left( p \right) = \frac{{pf}}{{p - f}}\) với \(p \in \left( {f; + \infty } \right)\).
b) \(\mathop {\lim }\limits_{p \to + \infty } g\left( p \right) = \mathop {\lim }\limits_{p \to + \infty } \frac{{pf}}{{p - f}} = \mathop {\lim }\limits_{p \to + \infty } \frac{f}{{1 - \frac{f}{p}}} = f,\mathop {\lim }\limits_{p \to {f^ + }} g\left( p \right) = \mathop {\lim }\limits_{p \to {f^ + }} \frac{{pf}}{{p - f}} = + \infty \)
Ý nghĩa của \(\mathop {\lim }\limits_{p \to + \infty } g\left( p \right) = f\): Khoảng cách từ vật đến thấu kính tiến ra vô cùng thì khoảng cách từ ảnh đến thấu kính xấp xỉ tiêu cự.
Ý nghĩa của \(\mathop {\lim }\limits_{p \to {f^ + }} g\left( p \right) = + \infty \): Khoảng cách từ vật đến thấu kính tiến gần về tiêu cự f thì khoảng cách từ ảnh đến thấu kính là càng lớn.
c) Ta có: \(q' = g'\left( p \right) = \frac{{ - {f^2}}}{{{{\left( {p - f} \right)}^2}}} < 0\;\forall p \in \left( {f; + \infty } \right)\) nên hàm số nghịch biến trên \(\left( {f; + \infty } \right)\).
Bảng biến thiên:
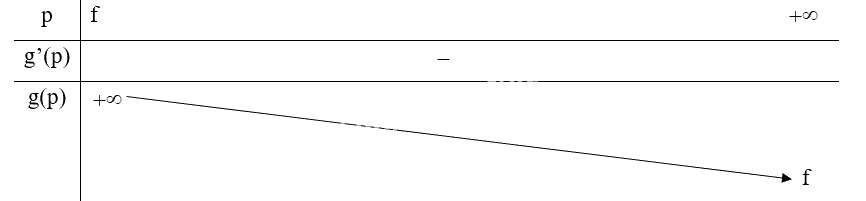
Bài tập 1.44 SGK Toán 12 tập 1 Kết nối tri thức là một bài toán quan trọng giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của đạo hàm trong việc giải quyết các bài toán thực tế. Dưới đây là hướng dẫn giải chi tiết bài tập này:
Cho hàm số f(x) = x3 - 3x2 + 2. Tìm các điểm cực trị của hàm số.
f'(x) = 3x2 - 6x
f'(x) = 0 ⇔ 3x2 - 6x = 0 ⇔ 3x(x - 2) = 0
Vậy, x = 0 hoặc x = 2
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| f'(x) | + | - | + | |
| f(x) | Đồng biến | Nghịch biến | Đồng biến |
Hàm số f(x) đạt cực đại tại x = 0, giá trị cực đại là f(0) = 2.
Hàm số f(x) đạt cực tiểu tại x = 2, giá trị cực tiểu là f(2) = -2.
Bài tập 1.44 là một ví dụ điển hình về việc ứng dụng đạo hàm để tìm cực trị của hàm số. Trong thực tế, việc tìm cực trị của hàm số có nhiều ứng dụng quan trọng trong các lĩnh vực như kinh tế, kỹ thuật và khoa học tự nhiên.
Để nắm vững kiến thức về đạo hàm và ứng dụng của đạo hàm, các em học sinh nên luyện tập thêm các bài tập tương tự trong SGK và các tài liệu tham khảo khác. Giaitoan.edu.vn sẽ tiếp tục cung cấp các bài giải chi tiết và hướng dẫn giải các bài tập Toán 12 khác.
Tìm các điểm cực trị của hàm số g(x) = x4 - 4x2 + 3.
Lưu ý: Bài giải trên chỉ mang tính chất tham khảo. Các em học sinh nên tự mình giải bài tập để hiểu rõ hơn về kiến thức và rèn luyện kỹ năng giải toán.
