Giải mục 1 trang 81,82 SGK Toán 12 tập 2 - Kết nối tri thức

Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 tại giaitoan.edu.vn. Chúng tôi xin giới thiệu lời giải chi tiết và dễ hiểu cho mục 1 trang 81,82 sách giáo khoa Toán 12 tập 2 chương trình Kết nối tri thức.

Bài viết này sẽ giúp các em nắm vững kiến thức, hiểu rõ phương pháp giải và tự tin làm bài tập.

TÍNH NGUYÊN HÀM VÀ TÍCH PHÂN VỚI PHẦN MỀM GEOGEBRA

Đề bài

Trả lời câu hỏi Thực hành 1 trang 82 SGK Toán 12 Kết nối tri thức

Sử dụng phần mềm GeoGebra, tính

a) \(\int {\frac{{{x^2} - 2x + 2}}{{x + 1}}dx} \);

b) \(\int\limits_0^{\frac{\pi }{2}} {{e^x}\cos 2x\;dx} \).

Phương pháp giải - Xem chi tiết Giải mục 1 trang 81,82 SGK Toán 12 tập 2 - Kết nối tri thức 1

Sử dụng kiến thức về các cú pháp lệnh trong GeoGebra để thực hiện:

Khởi động phần mềm Geogebra, chọn Complex Adaptive System (CAS) để thực hiện tính nguyên hàm và tích phân

Giải mục 1 trang 81,82 SGK Toán 12 tập 2 - Kết nối tri thức 2

Lời giải chi tiết

a) Khởi động phần mềm Geogebra, chọn Complex Adaptive System (CAS) để thực hiện tính nguyên hàm.

Để tính nguyên hàm của hàm số, ta dùng lệnh IntegralSymbolic (<hàm số>), kết quả sẽ được hiển thị ngay bên dưới

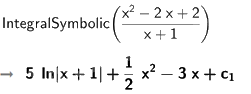
Giải mục 1 trang 81,82 SGK Toán 12 tập 2 - Kết nối tri thức 3

b) Khởi động phần mềm Geogebra, chọn Complex Adaptive System (CAS) để thực hiện tính nguyên hàm.

Để tính gần đúng tích phân, ta dùng lệnh TíchPhânXácĐịnh (<hàm số, giá trị đầu, giá trị cuối>), kết quả sẽ được hiển thị ngay bên dưới

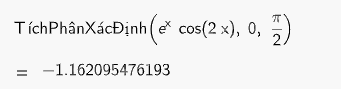
Giải mục 1 trang 81,82 SGK Toán 12 tập 2 - Kết nối tri thức 4

Tự tin bứt phá Kỳ thi THPT Quốc gia môn Toán! Đừng bỏ lỡ Giải mục 1 trang 81,82 SGK Toán 12 tập 2 - Kết nối tri thức đặc sắc thuộc chuyên mục đề toán lớp 12 trên nền tảng toán math. Với bộ bài tập toán thpt được biên soạn chuyên sâu, bám sát cấu trúc đề thi và chương trình Toán 12, đây chính là "chiến lược vàng" giúp các em tối ưu hóa ôn luyện. Học sinh sẽ không chỉ làm chủ mọi dạng bài thi mà còn nắm vững chiến thuật làm bài hiệu quả, sẵn sàng tự tin chinh phục điểm cao, vững bước vào đại học mơ ước nhờ phương pháp học trực quan, khoa học và hiệu quả học tập vượt trội!

Giải mục 1 trang 81,82 SGK Toán 12 tập 2 - Kết nối tri thức: Tổng quan

Mục 1 trang 81,82 SGK Toán 12 tập 2 - Kết nối tri thức tập trung vào việc ôn tập chương trình Giải tích, bao gồm các kiến thức về đạo hàm, tích phân và ứng dụng của chúng. Việc nắm vững các khái niệm và kỹ năng này là nền tảng quan trọng để giải quyết các bài toán phức tạp hơn trong chương trình học.

Nội dung chi tiết các bài tập trong mục 1

Mục 1 bao gồm một số bài tập trắc nghiệm và tự luận, yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các vấn đề cụ thể. Dưới đây là phân tích chi tiết từng bài tập:

Bài 1: Trắc nghiệm

Bài 1 thường tập trung vào việc kiểm tra khả năng hiểu các khái niệm cơ bản về đạo hàm và tích phân. Các câu hỏi có thể yêu cầu học sinh xác định đạo hàm của một hàm số, tính tích phân của một hàm số, hoặc tìm điểm cực trị của một hàm số.

Câu 1: (Ví dụ) Cho hàm số y = x³ - 3x² + 2. Tìm đạo hàm của hàm số.
Câu 2: (Ví dụ) Tính tích phân ∫₀¹ x² dx.

Bài 2: Tự luận

Bài 2 thường yêu cầu học sinh giải các bài toán phức tạp hơn, đòi hỏi sự vận dụng linh hoạt của kiến thức và kỹ năng. Các bài toán có thể liên quan đến việc tìm cực trị của hàm số, tính diện tích hình phẳng, hoặc giải phương trình vi phân.

Bài 2a: (Ví dụ) Tìm cực trị của hàm số y = x⁴ - 4x³ + 4x².
Bài 2b: (Ví dụ) Tính diện tích hình phẳng giới hạn bởi đường cong y = x² và đường thẳng y = 4.

Phương pháp giải các bài tập trong mục 1

Để giải các bài tập trong mục 1 một cách hiệu quả, học sinh cần nắm vững các phương pháp sau:

Phương pháp đạo hàm: Sử dụng đạo hàm để tìm cực trị, khoảng đơn điệu và điểm uốn của hàm số.
Phương pháp tích phân: Sử dụng tích phân để tính diện tích hình phẳng, thể tích vật thể và giải các bài toán liên quan đến tốc độ biến thiên.
Phương pháp biến đổi: Sử dụng các phép biến đổi đại số và lượng giác để đơn giản hóa bài toán và tìm ra lời giải.

Ví dụ minh họa lời giải chi tiết

Ví dụ: Giải bài toán tìm cực trị của hàm số y = x³ - 3x² + 2.

Lời giải:

Tính đạo hàm bậc nhất: y' = 3x² - 6x.
Tìm điểm cực trị: Giải phương trình y' = 0, ta được x = 0 hoặc x = 2.
Xác định loại cực trị: Tính đạo hàm bậc hai: y'' = 6x - 6.
Tại x = 0, y'' = -6 < 0, hàm số đạt cực đại tại x = 0, y_max = 2.
Tại x = 2, y'' = 6 > 0, hàm số đạt cực tiểu tại x = 2, y_min = -2.

Lưu ý khi giải bài tập

Khi giải bài tập trong mục 1, học sinh cần lưu ý những điều sau:

Đọc kỹ đề bài và xác định rõ yêu cầu của bài toán.
Vận dụng đúng các công thức và định lý đã học.
Kiểm tra lại kết quả để đảm bảo tính chính xác.
Luyện tập thường xuyên để nâng cao kỹ năng giải toán.

Tổng kết

Hy vọng rằng với những hướng dẫn chi tiết và ví dụ minh họa trên, các em học sinh sẽ tự tin giải quyết các bài tập trong mục 1 trang 81,82 SGK Toán 12 tập 2 - Kết nối tri thức. Chúc các em học tập tốt!