Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 12. Bài viết này sẽ hướng dẫn bạn cách giải bài tập 5.8 trang 39 SGK Toán 12 tập 2 - Kết nối tri thức một cách nhanh chóng và hiệu quả.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp bạn nắm vững kiến thức và đạt kết quả cao trong môn Toán.
Bác An dự định làm bốn mái của ngôi nhà sao cho chúng là bốn mặt bên của một hình chóp đều và các mái nhà kề nhau thì vuông góc với nhau. Hỏi ý tưởng trên có thực hiện được không?
Đề bài
Bác An dự định làm bốn mái của ngôi nhà sao cho chúng là bốn mặt bên của một hình chóp đều và các mái nhà kề nhau thì vuông góc với nhau. Hỏi ý tưởng trên có thực hiện được không?

Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về điều kiện để hai mặt phẳng vuông góc để chứng minh: Trong không gian Oxyz, cho hai mặt phẳng \(\left( \alpha \right):Ax + By + Cz + D = 0\), \(\left( \beta \right):A'x + B'y + C'z + D' = 0\) với hai vectơ pháp tuyến \(\overrightarrow n = \left( {A;B;C} \right),\overrightarrow {n'} = \left( {A';B';C'} \right)\) tương ứng. Khi đó, \(\left( \alpha \right) \bot \left( \beta \right) \Leftrightarrow \overrightarrow n \bot \overrightarrow {n'} \Leftrightarrow AA' + BB' + CC' = 0\)
Lời giải chi tiết
Đặt tên bốn mái của ngôi nhà và chọn hệ trục tọa độ như hình sau:
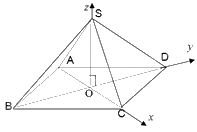
Giả sử hình vuông ABCD cạnh a và các cạnh bên bằng nhau có độ dài là b.
Vì ABCD là hình vuông, O là giao điểm của AC và BD nên \(OC = OD = OB = \frac{{a\sqrt 2 }}{2}\)
Tam giác SOC vuông tại O nên \(SO = \sqrt {S{C^2} - O{C^2}} = \sqrt {{b^2} - \frac{{{a^2}}}{2}} = \sqrt {\frac{{2{b^2} - {a^2}}}{2}} \)
Khi đó, \(O\left( {0;0;0} \right),C\left( {\frac{{a\sqrt 2 }}{2};0;0} \right),D\left( {0;\frac{{a\sqrt 2 }}{2};0} \right),B\left( {0;\frac{{ - a\sqrt 2 }}{2};0} \right),S\left( {0;0;\sqrt {\frac{{2{b^2} - {a^2}}}{2}} } \right)\)
\(\overrightarrow {SC} \left( {\frac{{a\sqrt 2 }}{2};0; - \sqrt {\frac{{2{b^2} - {a^2}}}{2}} } \right),\overrightarrow {DC} \left( {\frac{{a\sqrt 2 }}{2};\frac{{ - a\sqrt 2 }}{2};0} \right),\overrightarrow {BC} \left( {\frac{{a\sqrt 2 }}{2};\frac{{a\sqrt 2 }}{2};0} \right)\)
\(\left[ {\overrightarrow {SC} ,\frac{{\sqrt 2 }}{a}\overrightarrow {DC} } \right] = \left( {\left| {\begin{array}{*{20}{c}}0&{ - \sqrt {\frac{{2{b^2} - {a^2}}}{2}} }\\{ - 1}&0\end{array}} \right|,\left| {\begin{array}{*{20}{c}}{ - \sqrt {\frac{{2{b^2} - {a^2}}}{2}} }&{\frac{{a\sqrt 2 }}{2}}\\0&1\end{array}} \right|,\left| {\begin{array}{*{20}{c}}{\frac{{a\sqrt 2 }}{2}}&0\\1&{ - 1}\end{array}} \right|} \right)\) \( = \left( { - \sqrt {\frac{{2{b^2} - {a^2}}}{2}} ; - \sqrt {\frac{{2{b^2} - {a^2}}}{2}} ;\frac{{ - a\sqrt 2 }}{2}} \right)\)
\(\left[ {\overrightarrow {SC} ,\frac{{\sqrt 2 }}{a}\overrightarrow {BC} } \right] = \left( {\left| {\begin{array}{*{20}{c}}0&{ - \sqrt {\frac{{2{b^2} - {a^2}}}{2}} }\\1&0\end{array}} \right|,\left| {\begin{array}{*{20}{c}}{ - \sqrt {\frac{{2{b^2} - {a^2}}}{2}} }&{\frac{{a\sqrt 2 }}{2}}\\0&1\end{array}} \right|,\left| {\begin{array}{*{20}{c}}{\frac{{a\sqrt 2 }}{2}}&0\\1&1\end{array}} \right|} \right) = \left( {\sqrt {\frac{{2{b^2} - {a^2}}}{2}} ; - \sqrt {\frac{{2{b^2} - {a^2}}}{2}} ;\frac{{a\sqrt 2 }}{2}} \right)\)
Mặt phẳng (SCD) nhận \(\overrightarrow {{n_1}} = \left[ {\overrightarrow {SC} ,\frac{{\sqrt 2 }}{a}\overrightarrow {DC} } \right] = \left( { - \sqrt {\frac{{2{b^2} - {a^2}}}{2}} ; - \sqrt {\frac{{2{b^2} - {a^2}}}{2}} ;\frac{{ - a\sqrt 2 }}{2}} \right)\) làm một vectơ pháp tuyến.
Mặt phẳng (SCB) nhận \(\overrightarrow {{n_2}} = \left[ {\overrightarrow {SC} ,\frac{{\sqrt 2 }}{a}\overrightarrow {BC} } \right] = \left( {\sqrt {\frac{{2{b^2} - {a^2}}}{2}} ; - \sqrt {\frac{{2{b^2} - {a^2}}}{2}} ;\frac{{a\sqrt 2 }}{2}} \right)\) làm một vectơ pháp tuyến.
Ta có: \(\overrightarrow {{n_1}} .\overrightarrow {{n_2}} = - \sqrt {\frac{{2{b^2} - {a^2}}}{2}} .\sqrt {\frac{{2{b^2} - {a^2}}}{2}} + \sqrt {\frac{{2{b^2} - {a^2}}}{2}} .\sqrt {\frac{{2{b^2} - {a^2}}}{2}} + \frac{{a\sqrt 2 }}{2}.\frac{{a\sqrt 2 }}{2} = \frac{{{a^2}}}{2} \ne 0\)
Do đó, hai mặt phẳng (SCD) và (SCB) không vuông góc với nhau.
Vậy không thể thực hiện được ý tưởng trên.
Bài tập 5.8 trang 39 SGK Toán 12 tập 2 - Kết nối tri thức thuộc chương trình học về đạo hàm. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức về đạo hàm của hàm số, đạo hàm của tổng, hiệu, tích, thương của các hàm số để giải quyết các bài toán cụ thể. Việc nắm vững các quy tắc đạo hàm và kỹ năng biến đổi đại số là rất quan trọng để hoàn thành bài tập này.
Bài tập 5.8 thường có dạng như sau: Cho hàm số f(x) = ... (một biểu thức đại số). Hãy tính đạo hàm f'(x) của hàm số đó. Hoặc, bài tập có thể yêu cầu tìm đạo hàm cấp hai f''(x) hoặc giải các phương trình, bất phương trình liên quan đến đạo hàm.
Để giải bài tập 5.8, bạn cần thực hiện các bước sau:
Ví dụ: Tính đạo hàm của hàm số f(x) = 3x2 + 2x - 1.
Giải:
f'(x) = d/dx (3x2) + d/dx (2x) - d/dx (1)
f'(x) = 3 * 2x + 2 - 0
f'(x) = 6x + 2
Để củng cố kiến thức, bạn có thể tự giải các bài tập tương tự sau:
Bài tập 5.8 trang 39 SGK Toán 12 tập 2 - Kết nối tri thức là một bài tập quan trọng giúp bạn rèn luyện kỹ năng tính đạo hàm. Hy vọng với hướng dẫn chi tiết và ví dụ minh họa trên, bạn đã có thể tự tin giải quyết bài tập này một cách hiệu quả. Chúc bạn học tập tốt!