Chào mừng các em học sinh đến với bài giải chi tiết mục 3 trang 52,53 SGK Toán 12 tập 2 chương trình Kết nối tri thức. Bài viết này cung cấp lời giải đầy đủ, dễ hiểu cho từng bài tập, giúp các em nắm vững kiến thức và tự tin làm bài tập về nhà.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán, cung cấp các tài liệu học tập chất lượng và phương pháp giải bài tập hiệu quả.
CÔNG THỨC TÍNH GÓC GIỮA HAI MẶT PHẲNG
Trả lời câu hỏi Vận dụng trang 53 SGK Toán 12 Kết nối tri thức
Hãy trả lời câu hỏi đã được nêu ra trong tình huống mở đầu.
Phương pháp giải:
Sử dụng kiến thức về góc giữa hai mặt phẳng để tính: Trong không gian Oxyz, cho hai mặt phẳng (P), (Q) tương ứng có các vectơ pháp tuyến là \(\overrightarrow n = \left( {A;B;C} \right),\overrightarrow {n'} = \left( {A';B';C'} \right)\). Khi đó, góc giữa (P) và (Q), kí hiệu là ((P), (Q)) được tính theo công thức:
\(\cos \left( {\left( P \right),\left( Q \right)} \right) = \left| {\cos \left( {\overrightarrow n ,\overrightarrow {n'} } \right)} \right| = \frac{{\left| {AA' + BB' + CC'} \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} .\sqrt {A{'^2} + B{'^2} + C{'^2}} }}\)
Lời giải chi tiết:
Ta có: \(A\left( {0; - 2;0} \right),C\left( {0;2;0} \right),B\left( {2\sqrt 3 ;0;0} \right),A'\left( {0; - 2;7} \right),C'\left( {0;2;5} \right),B'\left( {2\sqrt 3 ;0;6} \right)\)
\(\overrightarrow {AB} \left( {2\sqrt 3 ;2;0} \right),\overrightarrow {AC} \left( {0;4;0} \right);\overrightarrow {A'B'} \left( {2\sqrt 3 ;2; - 1} \right),\overrightarrow {A'C'} \left( {0;4; - 2} \right)\)
\(\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = \left( {\left| {\begin{array}{*{20}{c}}2&0\\4&0\end{array}} \right|,\left| {\begin{array}{*{20}{c}}0&{2\sqrt 3 }\\0&0\end{array}} \right|,\left| {\begin{array}{*{20}{c}}{2\sqrt 3 }&2\\0&4\end{array}} \right|} \right) = \left( {0;0; 8\sqrt 3 } \right)\)
\(\left[ {\overrightarrow {A'B'} ,\overrightarrow {A'C'} } \right] = \left( {\left| {\begin{array}{*{20}{c}}2&{ - 1}\\4&{ - 2}\end{array}} \right|,\left| {\begin{array}{*{20}{c}}{ - 1}&{2\sqrt 3 }\\{ - 2}&0\end{array}} \right|,\left| {\begin{array}{*{20}{c}}{2\sqrt 3 }&2\\0&4\end{array}} \right|} \right) = \left( {0;4\sqrt 3 ;8\sqrt 3 } \right)\)
Mặt phẳng (ABC) có một vectơ pháp tuyến là: \(\frac{{ 1}}{{8\sqrt 3 }}\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = \left( {0;0;1} \right)\)
Mặt phẳng (A’B’C’) có một vectơ pháp tuyến là: \(\frac{1}{{4\sqrt 3 }}\left[ {\overrightarrow {A'B'} ,\overrightarrow {A'C'} } \right] = \left( {0;1;2} \right)\)
Do đó, \(\cos \left( {\left( {ABC} \right),\left( {A'B'C'} \right)} \right) = \frac{{\left| {0.0 + 0.1 + 1.2} \right|}}{{\sqrt {{0^2} + {0^2} + {1^2}} .\sqrt {{0^2} + {1^2} + {2^2}} }} = \frac{{2\sqrt 5 }}{5}\)
\( \Rightarrow \left( {\left( {ABC} \right),\left( {A'B'C'} \right)} \right) \approx 26,{6^o}\)
Vậy mái nhà nghiêng so với mặt sàn nhà một góc khoảng \(26,{1^o}\).
Trả lời câu hỏi Luyện tập 3 trang 52 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, tính góc giữa hai mặt phẳng \(\left( P \right):x - \sqrt 2 y + z - 2 = 0\) và \(\left( {Oxz} \right):y = 0\).
Phương pháp giải:
Sử dụng kiến thức về góc giữa hai mặt phẳng để tính: Trong không gian Oxyz, cho hai mặt phẳng (P), (Q) tương ứng có các vectơ pháp tuyến là \(\overrightarrow n = \left( {A;B;C} \right),\overrightarrow {n'} = \left( {A';B';C'} \right)\). Khi đó, góc giữa (P) và (Q), kí hiệu là ((P), (Q)) được tính theo công thức:
\(\cos \left( {\left( P \right),\left( Q \right)} \right) = \left| {\cos \left( {\overrightarrow n ,\overrightarrow {n'} } \right)} \right| = \frac{{\left| {AA' + BB' + CC'} \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} .\sqrt {A{'^2} + B{'^2} + C{'^2}} }}\).
Lời giải chi tiết:
Mặt phẳng (P) có vectơ pháp tuyến là \(\overrightarrow n \left( {1; - \sqrt 2 ;1} \right)\), mặt phẳng (Oxz) có vectơ pháp tuyến là \(\overrightarrow n \left( {0;1;0} \right)\). Ta có: \(\cos \left( {\left( P \right),\left( Q \right)} \right) = \frac{{\left| {0.1 - \sqrt 2 .1 + 1.0} \right|}}{{\sqrt {{0^2} + {0^2} + {1^2}} .\sqrt {{1^2} + {{\left( { - \sqrt 2 } \right)}^2} + {1^2}} }} = \frac{{\sqrt 2 }}{2}\)
Do đó, \(\left( {\left( P \right),\left( {Oxz} \right)} \right) = {45^0}\).
Trả lời câu hỏi Hoạt động 3 trang 52 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, cho hai mặt phẳng (P), (Q) tương ứng có các vectơ pháp tuyến là \(\overrightarrow n = \left( {A;B;C} \right),\overrightarrow {n'} = \left( {A';B';C'} \right)\). Lấy các đường thẳng \(\Delta \), \(\Delta '\) tương ứng có vectơ chỉ phương \(\overrightarrow n ,\overrightarrow {n'} \) (H.5.36)
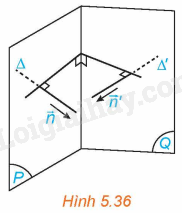
a) Góc giữa hai mặt phẳng (P) và (Q) và góc giữa hai đường thẳng \(\Delta \) và \(\Delta '\) có mối quan hệ gì?
b) Tính côsin của góc giữa hai mặt phẳng (P) và (Q).
Phương pháp giải:
Sử dụng kiến thức về góc giữa hai mặt phẳng để tìm mối quan hệ: Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt vuông góc với hai mặt phẳng đó.
Sử dụng kiến thức về góc giữa hai đường thẳng để tính: Trong không gian Oxyz, cho hai đường thẳng \(\Delta \) và \(\Delta '\) tương ứng có vectơ chỉ phương \(\overrightarrow u ,\overrightarrow {u'} \) thì \(\cos \left( {\Delta ,\Delta '} \right) = \left| {\cos \left( {\overrightarrow u ,\overrightarrow {u'} } \right)} \right|\).
Lời giải chi tiết:
a) Vì các đường thẳng \(\Delta \), \(\Delta '\) tương ứng có vectơ chỉ phương \(\overrightarrow n ,\overrightarrow {n'} \) nên đường thẳng \(\Delta \) vuông góc với mặt phẳng (P), đường thẳng \(\Delta '\) vuông góc với mặt phẳng (Q).
Do đó, \(\left( {\left( P \right),\left( Q \right)} \right) = \left( {\Delta ,\Delta '} \right)\)
b) Ta có: \(\cos \left( {\Delta ,\Delta '} \right) = \left| {\cos \left( {\overrightarrow n ,\overrightarrow {n'} } \right)} \right|\) nên \(\cos \left( {\left( P \right),\left( Q \right)} \right) = \cos \left( {\Delta ,\Delta '} \right) = \left| {\cos \left( {\overrightarrow n ,\overrightarrow {n'} } \right)} \right|\).
Trả lời câu hỏi Hoạt động 3 trang 52 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, cho hai mặt phẳng (P), (Q) tương ứng có các vectơ pháp tuyến là \(\overrightarrow n = \left( {A;B;C} \right),\overrightarrow {n'} = \left( {A';B';C'} \right)\). Lấy các đường thẳng \(\Delta \), \(\Delta '\) tương ứng có vectơ chỉ phương \(\overrightarrow n ,\overrightarrow {n'} \) (H.5.36)
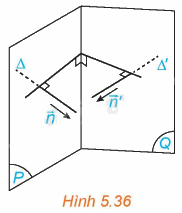
a) Góc giữa hai mặt phẳng (P) và (Q) và góc giữa hai đường thẳng \(\Delta \) và \(\Delta '\) có mối quan hệ gì?
b) Tính côsin của góc giữa hai mặt phẳng (P) và (Q).
Phương pháp giải:
Sử dụng kiến thức về góc giữa hai mặt phẳng để tìm mối quan hệ: Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt vuông góc với hai mặt phẳng đó.
Sử dụng kiến thức về góc giữa hai đường thẳng để tính: Trong không gian Oxyz, cho hai đường thẳng \(\Delta \) và \(\Delta '\) tương ứng có vectơ chỉ phương \(\overrightarrow u ,\overrightarrow {u'} \) thì \(\cos \left( {\Delta ,\Delta '} \right) = \left| {\cos \left( {\overrightarrow u ,\overrightarrow {u'} } \right)} \right|\).
Lời giải chi tiết:
a) Vì các đường thẳng \(\Delta \), \(\Delta '\) tương ứng có vectơ chỉ phương \(\overrightarrow n ,\overrightarrow {n'} \) nên đường thẳng \(\Delta \) vuông góc với mặt phẳng (P), đường thẳng \(\Delta '\) vuông góc với mặt phẳng (Q).
Do đó, \(\left( {\left( P \right),\left( Q \right)} \right) = \left( {\Delta ,\Delta '} \right)\)
b) Ta có: \(\cos \left( {\Delta ,\Delta '} \right) = \left| {\cos \left( {\overrightarrow n ,\overrightarrow {n'} } \right)} \right|\) nên \(\cos \left( {\left( P \right),\left( Q \right)} \right) = \cos \left( {\Delta ,\Delta '} \right) = \left| {\cos \left( {\overrightarrow n ,\overrightarrow {n'} } \right)} \right|\).
Trả lời câu hỏi Luyện tập 3 trang 52 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, tính góc giữa hai mặt phẳng \(\left( P \right):x - \sqrt 2 y + z - 2 = 0\) và \(\left( {Oxz} \right):y = 0\).
Phương pháp giải:
Sử dụng kiến thức về góc giữa hai mặt phẳng để tính: Trong không gian Oxyz, cho hai mặt phẳng (P), (Q) tương ứng có các vectơ pháp tuyến là \(\overrightarrow n = \left( {A;B;C} \right),\overrightarrow {n'} = \left( {A';B';C'} \right)\). Khi đó, góc giữa (P) và (Q), kí hiệu là ((P), (Q)) được tính theo công thức:
\(\cos \left( {\left( P \right),\left( Q \right)} \right) = \left| {\cos \left( {\overrightarrow n ,\overrightarrow {n'} } \right)} \right| = \frac{{\left| {AA' + BB' + CC'} \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} .\sqrt {A{'^2} + B{'^2} + C{'^2}} }}\).
Lời giải chi tiết:
Mặt phẳng (P) có vectơ pháp tuyến là \(\overrightarrow n \left( {1; - \sqrt 2 ;1} \right)\), mặt phẳng (Oxz) có vectơ pháp tuyến là \(\overrightarrow n \left( {0;1;0} \right)\). Ta có: \(\cos \left( {\left( P \right),\left( Q \right)} \right) = \frac{{\left| {0.1 - \sqrt 2 .1 + 1.0} \right|}}{{\sqrt {{0^2} + {0^2} + {1^2}} .\sqrt {{1^2} + {{\left( { - \sqrt 2 } \right)}^2} + {1^2}} }} = \frac{{\sqrt 2 }}{2}\)
Do đó, \(\left( {\left( P \right),\left( {Oxz} \right)} \right) = {45^0}\).
Trả lời câu hỏi Vận dụng trang 53 SGK Toán 12 Kết nối tri thức
Hãy trả lời câu hỏi đã được nêu ra trong tình huống mở đầu.
Phương pháp giải:
Sử dụng kiến thức về góc giữa hai mặt phẳng để tính: Trong không gian Oxyz, cho hai mặt phẳng (P), (Q) tương ứng có các vectơ pháp tuyến là \(\overrightarrow n = \left( {A;B;C} \right),\overrightarrow {n'} = \left( {A';B';C'} \right)\). Khi đó, góc giữa (P) và (Q), kí hiệu là ((P), (Q)) được tính theo công thức:
\(\cos \left( {\left( P \right),\left( Q \right)} \right) = \left| {\cos \left( {\overrightarrow n ,\overrightarrow {n'} } \right)} \right| = \frac{{\left| {AA' + BB' + CC'} \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} .\sqrt {A{'^2} + B{'^2} + C{'^2}} }}\)
Lời giải chi tiết:
Ta có: \(A\left( {0; - 2;0} \right),C\left( {0;2;0} \right),B\left( {2\sqrt 3 ;0;0} \right),A'\left( {0; - 2;7} \right),C'\left( {0;2;5} \right),B'\left( {2\sqrt 3 ;0;6} \right)\)
\(\overrightarrow {AB} \left( {2\sqrt 3 ;2;0} \right),\overrightarrow {AC} \left( {0;4;0} \right);\overrightarrow {A'B'} \left( {2\sqrt 3 ;2; - 1} \right),\overrightarrow {A'C'} \left( {0;4; - 2} \right)\)
\(\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = \left( {\left| {\begin{array}{*{20}{c}}2&0\\4&0\end{array}} \right|,\left| {\begin{array}{*{20}{c}}0&{2\sqrt 3 }\\0&0\end{array}} \right|,\left| {\begin{array}{*{20}{c}}{2\sqrt 3 }&2\\0&4\end{array}} \right|} \right) = \left( {0;0; 8\sqrt 3 } \right)\)
\(\left[ {\overrightarrow {A'B'} ,\overrightarrow {A'C'} } \right] = \left( {\left| {\begin{array}{*{20}{c}}2&{ - 1}\\4&{ - 2}\end{array}} \right|,\left| {\begin{array}{*{20}{c}}{ - 1}&{2\sqrt 3 }\\{ - 2}&0\end{array}} \right|,\left| {\begin{array}{*{20}{c}}{2\sqrt 3 }&2\\0&4\end{array}} \right|} \right) = \left( {0;4\sqrt 3 ;8\sqrt 3 } \right)\)
Mặt phẳng (ABC) có một vectơ pháp tuyến là: \(\frac{{ 1}}{{8\sqrt 3 }}\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = \left( {0;0;1} \right)\)
Mặt phẳng (A’B’C’) có một vectơ pháp tuyến là: \(\frac{1}{{4\sqrt 3 }}\left[ {\overrightarrow {A'B'} ,\overrightarrow {A'C'} } \right] = \left( {0;1;2} \right)\)
Do đó, \(\cos \left( {\left( {ABC} \right),\left( {A'B'C'} \right)} \right) = \frac{{\left| {0.0 + 0.1 + 1.2} \right|}}{{\sqrt {{0^2} + {0^2} + {1^2}} .\sqrt {{0^2} + {1^2} + {2^2}} }} = \frac{{2\sqrt 5 }}{5}\)
\( \Rightarrow \left( {\left( {ABC} \right),\left( {A'B'C'} \right)} \right) \approx 26,{6^o}\)
Vậy mái nhà nghiêng so với mặt sàn nhà một góc khoảng \(26,{1^o}\).
Mục 3 trong SGK Toán 12 tập 2 Kết nối tri thức thường tập trung vào một chủ đề cụ thể trong chương trình học. Để giải quyết các bài tập trong mục này một cách hiệu quả, học sinh cần nắm vững lý thuyết, công thức và phương pháp giải liên quan. Bài viết này sẽ cung cấp lời giải chi tiết cho từng bài tập, đồng thời giải thích rõ ràng các bước thực hiện để giúp học sinh hiểu sâu sắc kiến thức.
Thông thường, Mục 3 trang 52,53 SGK Toán 12 tập 2 Kết nối tri thức sẽ bao gồm các dạng bài tập sau:
Đề bài: (Giả định một đề bài cụ thể từ SGK)
Lời giải:
Kết luận: (Kết quả của bài tập)
Đề bài: (Giả định một đề bài cụ thể từ SGK)
Lời giải:
Kết luận: (Kết quả của bài tập)
Đề bài: (Giả định một đề bài cụ thể từ SGK)
Lời giải:
Kết luận: (Kết quả của bài tập)
Để giải bài tập Toán 12 tập 2 Kết nối tri thức một cách hiệu quả, các em có thể tham khảo một số mẹo sau:
Ngoài SGK, các em có thể tham khảo thêm các tài liệu sau để học Toán 12 tập 2 Kết nối tri thức:
Hy vọng bài giải chi tiết mục 3 trang 52,53 SGK Toán 12 tập 2 Kết nối tri thức này sẽ giúp các em học sinh hiểu rõ hơn về kiến thức và tự tin làm bài tập. Chúc các em học tập tốt!