Bài viết này cung cấp đầy đủ lý thuyết và công thức tính góc trong không gian, một chủ đề quan trọng trong chương trình Toán 12 Kết nối tri thức. Chúng tôi sẽ trình bày một cách dễ hiểu, kèm theo các ví dụ minh họa để bạn có thể nắm vững kiến thức.
Nội dung bao gồm các khái niệm cơ bản về góc giữa hai đường thẳng, góc giữa đường thẳng và mặt phẳng, góc nhị diện, cùng với các công thức tính toán chi tiết.
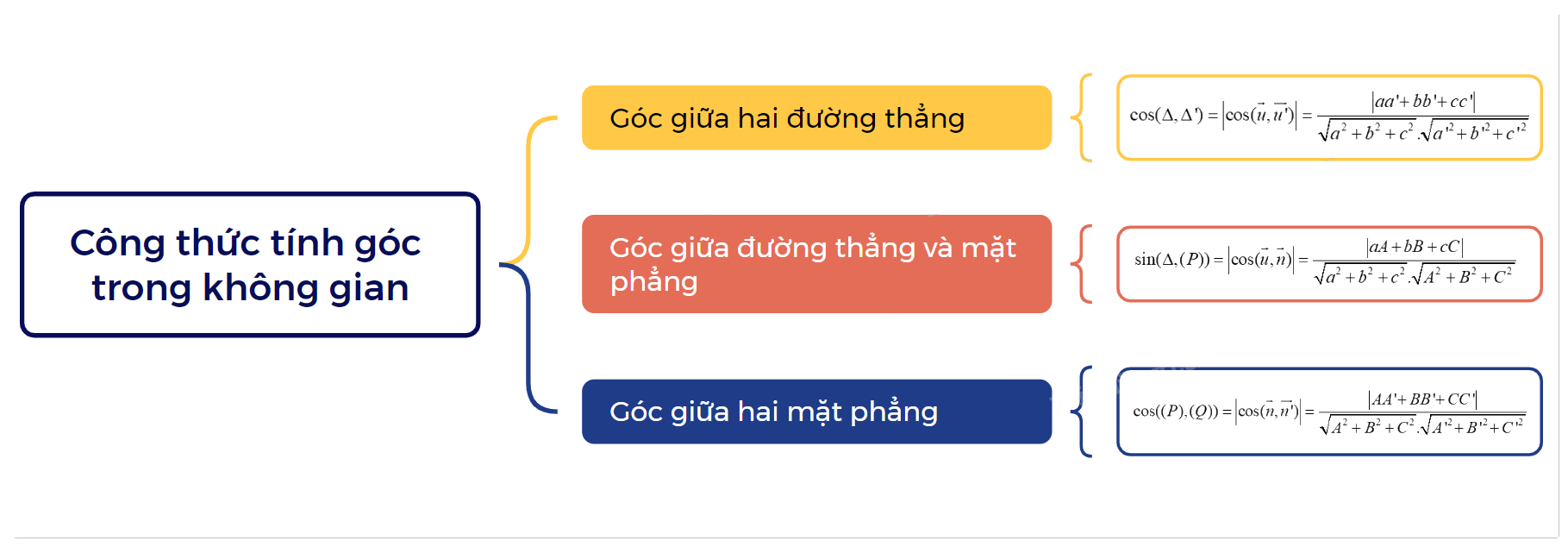
1. Công thức tính góc giữa hai đường thẳng
1. Công thức tính góc giữa hai đường thẳng
Trong không gian Oxyz, cho hai đường thẳng \(\Delta \) và \(\Delta '\) tương ứng có vecto chỉ phương \(\overrightarrow u = (a;b;c),\overrightarrow {u'} = (a';b';c')\). Khi đó: \(\cos (\Delta ,\Delta ') = \left| {\cos (\overrightarrow u ,\overrightarrow {u'} )} \right| = \frac{{\left| {aa' + bb' + cc'} \right|}}{{\sqrt {{a^2} + {b^2} + {c^2}} .\sqrt {a{'^2} + b{'^2} + c{'^2}} }}\) |
2. Công thức tính góc giữa đường thẳng và mặt phẳng
Trong không gian Oxyz, cho đường thẳng \(\Delta \) có vecto chỉ phương \(\overrightarrow u = (a;b;c)\) và mặt phẳng (P) có vecto pháp tuyến \(\overrightarrow n = (A;B;C)\). Khi đó: \(\sin (\Delta ,(P)) = \left| {\cos (\overrightarrow u ,\overrightarrow n )} \right| = \frac{{\left| {aA + bB + cC} \right|}}{{\sqrt {{a^2} + {b^2} + {c^2}} .\sqrt {{A^2} + {B^2} + {C^2}} }}\) |
3. Công thức tính góc giữa hai mặt phẳng
Trong không gian Oxyz, cho hai mặt phẳng (P), (Q) tương ứng có các vecto pháp tuyến \(\overrightarrow n = (A;B;C),\overrightarrow {n'} = (A';B';C')\). Khi đó, góc giữa (P) và (Q), kí hiệu là ((P), (Q)), được tính theo công thức: \(\cos ((P),(Q)) = \left| {\cos (\overrightarrow n ,\overrightarrow {n'} )} \right| = \frac{{\left| {AA' + BB' + CC'} \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} .\sqrt {A{'^2} + B{'^2} + C{'^2}} }}\) |
Chương trình Toán 12 Kết nối tri thức, phần Hình học không gian, đặt ra những bài toán về góc giữa các đối tượng hình học trong không gian ba chiều. Việc nắm vững lý thuyết và công thức tính góc là vô cùng quan trọng để giải quyết các bài toán này một cách chính xác và hiệu quả. Bài viết này sẽ đi sâu vào các khái niệm, định nghĩa và công thức liên quan đến góc trong không gian, giúp bạn hiểu rõ và áp dụng chúng vào thực tế.
Để xác định góc giữa hai đường thẳng trong không gian, ta cần hiểu rõ khái niệm vectơ chỉ phương. Góc giữa hai đường thẳng là góc giữa hai vectơ chỉ phương của chúng.
Góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng đó và hình chiếu của nó lên mặt phẳng.
Góc nhị diện là góc tạo bởi hai nửa mặt phẳng có chung một đường thẳng. Để đo góc nhị diện, ta sử dụng góc giữa hai vectơ pháp tuyến của hai nửa mặt phẳng đó.
Ngoài các công thức cơ bản trên, còn có một số công thức và kỹ thuật hỗ trợ trong việc tính góc trong không gian:
Ví dụ 1: Cho hai đường thẳng d1: x = 1 + t, y = 2 - t, z = 3 + 2t" và d2: x = 2 - s, y = 1 + s, z = 4 - s". Tính góc giữa hai đường thẳng này.
Giải:
Vectơ chỉ phương của d1 là \vec{u_1} = (1, -1, 2)". Vectơ chỉ phương của d2 là \vec{u_2} = (-1, 1, -1)".
cos(\vec{u_1}, \vec{u_2}) = \frac{(1)(-1) + (-1)(1) + (2)(-1)}{\sqrt{1^2 + (-1)^2 + 2^2} \cdot \sqrt{(-1)^2 + 1^2 + (-1)^2}} = \frac{-4}{\sqrt{6} \cdot \sqrt{3}} = \frac{-4}{\sqrt{18}} = \frac{-4}{3\sqrt{2}} = \frac{-2\sqrt{2}}{3}"
Vậy góc giữa hai đường thẳng là arccos(\frac{-2\sqrt{2}}{3})".
Ví dụ 2: Cho mặt phẳng (P): 2x - y + z - 5 = 0" và đường thẳng d: x = 1 + t, y = 2 - t, z = 3 + t". Tính góc giữa đường thẳng d và mặt phẳng (P).
Giải:
Vectơ pháp tuyến của (P) là \vec{n} = (2, -1, 1)". Vectơ chỉ phương của d là \vec{u} = (1, -1, 1)".
sin(\vec{d}, (P)) = \frac{|(1)(2) + (-1)(-1) + (1)(1)|}{\sqrt{1^2 + (-1)^2 + 1^2} \cdot \sqrt{2^2 + (-1)^2 + 1^2}} = \frac{|2 + 1 + 1|}{\sqrt{3} \cdot \sqrt{6}} = \frac{4}{\sqrt{18}} = \frac{4}{3\sqrt{2}} = \frac{2\sqrt{2}}{3}"
Vậy góc giữa đường thẳng d và mặt phẳng (P) là arcsin(\frac{2\sqrt{2}}{3})".
Việc hiểu rõ lý thuyết và công thức tính góc trong không gian là nền tảng để giải quyết các bài toán hình học không gian trong chương trình Toán 12 Kết nối tri thức. Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cần thiết và hữu ích. Hãy luyện tập thêm nhiều bài tập để nắm vững kiến thức và kỹ năng giải toán.