Lý thuyết Hệ trục tọa độ trong không gian Toán 12 Kết nối tri thức

Chào mừng bạn đến với bài học về Lý thuyết Hệ trục tọa độ trong không gian, một phần quan trọng trong chương trình Toán 12 Kết nối tri thức. Bài học này sẽ cung cấp cho bạn những kiến thức nền tảng và các công thức cần thiết để giải quyết các bài toán liên quan đến hình học không gian.

Chúng ta sẽ cùng nhau tìm hiểu về hệ trục tọa độ, tọa độ của điểm và vector, các phép toán vector trong không gian, và ứng dụng của chúng trong việc xác định phương trình của đường thẳng và mặt phẳng.

1. Hệ trục tọa độ trong không gian

1. Hệ trục tọa độ trong không gian

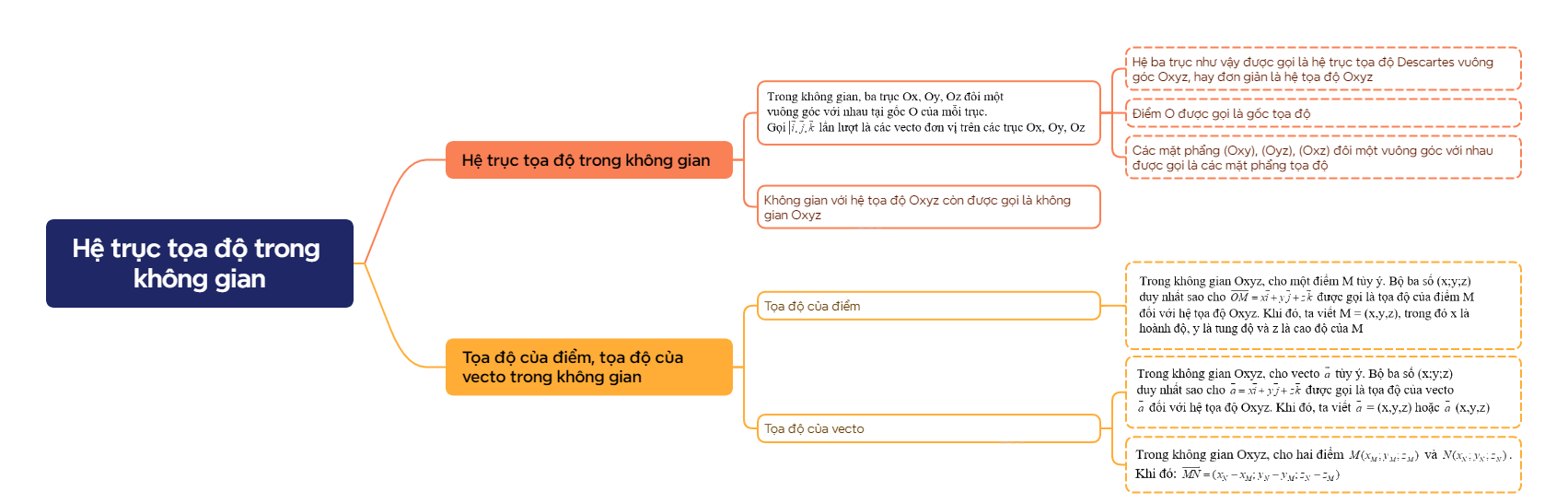
Trong không gian, ba trục Ox, Oy, Oz đôi một vuông góc với nhau tại gốc O của mỗi trục. Gọi \(\overrightarrow i ,\overrightarrow j ,\overrightarrow k \) lần lượt là các vecto đơn vị trên các trục Ox, Oy, Oz

- Hệ ba trục như vậy được gọi là hệ trục tọa độ Descartes vuông góc Oxyz, hay đơn giản là hệ tọa độ Oxyz

- Điểm O được gọi là gốc tọa độ

- Các mặt phẳng (Oxy), (Oyz), (Oxz) đôi một vuông góc với nhau được gọi là các mặt phẳng tọa độ

Không gian với hệ tọa độ Oxyz còn được gọi là không gian Oxyz

2. Tọa độ của điểm, tọa độ của vecto trong không gian

Tọa độ của điểm

Trong không gian Oxyz, cho một điểm M tùy ý. Bộ ba số (x;y;z) duy nhất sao cho \(\overrightarrow {OM} = x\overrightarrow i + y\overrightarrow j + z\overrightarrow k \) được gọi là tọa độ của điểm M đối với hệ tọa độ Oxyz. Khi đó, ta viết M = (x,y,z), trong đó x là hoành độ, y là tung độ và z là cao độ của M

Tọa độ của vecto

Trong không gian Oxyz, cho vecto \(\overrightarrow a \) tùy ý. Bộ ba số (x;y;z) duy nhất sao cho \(\overrightarrow a = x\overrightarrow i + y\overrightarrow j + z\overrightarrow k \) được gọi là tọa độ của vecto \(\overrightarrow a \) đối với hệ tọa độ Oxyz. Khi đó, ta viết \(\overrightarrow a \) = (x,y,z) hoặc \(\overrightarrow a \) (x,y,z)

Trong không gian Oxyz, cho hai điểm \(M({x_M};{y_M};{z_M})\) và \(N({x_N};{y_N};{z_N})\). Khi đó:

\(\overrightarrow {MN} = ({x_N} - {x_M};{y_N} - {y_M};{z_N} - {z_M})\)

Ví dụ: Trong không gian Oxyz, cho hình lăng trụ tam giác ABC.A’B’C có A(1;0;2), B(3;2;5), C(7;-3;9)

a) Tìm tọa độ của \(\overrightarrow {AA'} \)

b) Tìm tọa độ của các điểm B’, C’

Lời giải

a) Ta có: \(\overrightarrow {AA'} = ({x_{A'}} - {x_A};{y_{A'}} - {y_A};{z_{A'}} - {z_A}) = (4;0; - 1)\)

b) Gọi tọa độ của điểm B’ là (x,y,z) thì \(\overrightarrow {BB'} \) = (x-3;y-2;z-5). Vì ABC.A’B’C’ là hình lăng trụ nên ABB’A’ là hình bình hành, suy ra \(\overrightarrow {AA'} \) = \(\overrightarrow {BB'} \)

Do đó \(\left\{ \begin{array}{l}x - 3 = 4\\y - 2 = 0\\z - 5 = - 1\end{array} \right.\) hay x = 7, y = 2, z = 4. Vậy B’(7;2;4)

Lập luận tương tự suy ra C’(11;-3;8)

Lý thuyết Hệ trục tọa độ trong không gian Toán 12 Kết nối tri thức 1

Tự tin bứt phá Kỳ thi THPT Quốc gia môn Toán! Đừng bỏ lỡ Lý thuyết Hệ trục tọa độ trong không gian Toán 12 Kết nối tri thức đặc sắc thuộc chuyên mục giải sgk toán 12 trên nền tảng môn toán. Với bộ bài tập toán thpt được biên soạn chuyên sâu, bám sát cấu trúc đề thi và chương trình Toán 12, đây chính là "chiến lược vàng" giúp các em tối ưu hóa ôn luyện. Học sinh sẽ không chỉ làm chủ mọi dạng bài thi mà còn nắm vững chiến thuật làm bài hiệu quả, sẵn sàng tự tin chinh phục điểm cao, vững bước vào đại học mơ ước nhờ phương pháp học trực quan, khoa học và hiệu quả học tập vượt trội!

Lý thuyết Hệ trục tọa độ trong không gian Toán 12 Kết nối tri thức

Hệ trục tọa độ trong không gian là một công cụ quan trọng để mô tả vị trí của các điểm và vector trong không gian ba chiều. Nó bao gồm ba trục vuông góc với nhau, thường được ký hiệu là Ox, Oy và Oz. Giao điểm của ba trục này được gọi là gốc tọa độ O.

1. Hệ trục tọa độ Oxyz

Hệ trục tọa độ Oxyz được xác định bởi ba trục Ox, Oy, Oz. Mỗi điểm trong không gian có thể được xác định duy nhất bởi bộ ba số thực (x, y, z), gọi là tọa độ của điểm đó. Tọa độ x, y, z lần lượt là hình chiếu vuông góc của điểm lên các trục Ox, Oy, Oz.

2. Tọa độ của điểm và vector

Tọa độ của điểm: Nếu M là một điểm trong không gian, tọa độ của M là (x_M, y_M, z_M).

Tọa độ của vector: Nếu a là một vector trong không gian, tọa độ của a là (a_x, a_y, a_z).

3. Các phép toán vector trong không gian

Phép cộng vector:a + b = (a_x + b_x, a_y + b_y, a_z + b_z)
Phép trừ vector:a - b = (a_x - b_x, a_y - b_y, a_z - b_z)
Phép nhân vector với một số thực: ka = (ka_x, ka_y, ka_z)
Tích vô hướng của hai vector:a ⋅ b = a_xb_x + a_yb_y + a_zb_z
Tích có hướng của hai vector:a × b = (a_yb_z - a_zb_y, a_zb_x - a_xb_z, a_xb_y - a_yb_x)

4. Ứng dụng của hệ trục tọa độ trong không gian

Hệ trục tọa độ trong không gian được sử dụng để:

Xác định vị trí của các điểm và vật thể trong không gian.
Tính toán khoảng cách giữa các điểm.
Xác định góc giữa các đường thẳng và mặt phẳng.
Viết phương trình của đường thẳng và mặt phẳng.

5. Phương trình đường thẳng trong không gian

Có nhiều dạng phương trình để biểu diễn một đường thẳng trong không gian:

Phương trình tham số: x = x₀ + at y = y₀ + bt z = z₀ + ct (trong đó (x₀, y₀, z₀) là một điểm thuộc đường thẳng và (a, b, c) là vector chỉ phương của đường thẳng)
Phương trình chính tắc: (x - x₀)/a = (y - y₀)/b = (z - z₀)/c

6. Phương trình mặt phẳng trong không gian

Phương trình tổng quát của một mặt phẳng trong không gian có dạng:

Ax + By + Cz + D = 0 (trong đó (A, B, C) là vector pháp tuyến của mặt phẳng)

7. Bài tập ví dụ

Bài tập 1: Cho hai điểm A(1, 2, 3) và B(4, 5, 6). Tính độ dài đoạn thẳng AB.

Giải: AB = √((4-1)² + (5-2)² + (6-3)²) = √(3² + 3² + 3²) = √27 = 3√3

Bài tập 2: Tìm phương trình mặt phẳng đi qua điểm M(1, 2, 3) và có vector pháp tuyến n = (1, 1, 1).

Giải: Phương trình mặt phẳng là: 1(x - 1) + 1(y - 2) + 1(z - 3) = 0 => x + y + z - 6 = 0

Hy vọng bài học này đã cung cấp cho bạn những kiến thức cơ bản và hữu ích về Lý thuyết Hệ trục tọa độ trong không gian Toán 12 Kết nối tri thức. Chúc bạn học tốt!