Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 12. Bài viết này sẽ hướng dẫn bạn cách giải bài tập 5.50 trang 63 SGK Toán 12 tập 2 - Kết nối tri thức một cách nhanh chóng và hiệu quả.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp bạn nắm vững kiến thức và đạt kết quả cao trong môn Toán.
Từ mặt nước trong một bể nước, tại ba vị trí đôi một cách nhau 2m, người ta lần lượt thả dây dọi để quả dọi chạm đáy bể. Phần dây dọi (thẳng) nằm trong nước tại ba vị trí đó lần lượt có độ dài 4m; 4,4m; 4,8m. Biết đáy bể là phẳng. Hỏi đáy bể nghiêng so với mặt phẳng nằm ngang một góc bao nhiêu độ?
Đề bài
Từ mặt nước trong một bể nước, tại ba vị trí đôi một cách nhau 2 m, người ta lần lượt thả dây dọi để quả dọi chạm đáy bể. Phần dây dọi (thẳng) nằm trong nước tại ba vị trí đó lần lượt có độ dài 4 m; 4,4 m; 4,8 m. Biết đáy bể là phẳng. Hỏi đáy bể nghiêng so với mặt phẳng nằm ngang một góc bao nhiêu độ?
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về góc giữa hai mặt phẳng để tính: Trong không gian Oxyz, cho hai mặt phẳng (P), (Q) tương ứng có các vectơ pháp tuyến là \(\overrightarrow n = \left( {A;B;C} \right),\overrightarrow {n'} = \left( {A';B';C'} \right)\). Khi đó, góc giữa (P) và (Q), kí hiệu là ((P), (Q)) được tính theo công thức:
\(\cos \left( {\left( P \right),\left( Q \right)} \right) = \left| {\cos \left( {\overrightarrow n ,\overrightarrow {n'} } \right)} \right| = \frac{{\left| {AA' + BB' + CC'} \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} .\sqrt {A{'^2} + B{'^2} + C{'^2}} }}\).
Lời giải chi tiết
Gọi 3 điểm cách nhau 2m trên mặt nước là A, B, C. Vị trí thả quả rọi xuống đáy bể lần lượt là A’, B’, C’ sao cho AA' = 4 m, BB' = 4,4 m, CC' = 4,8 m. Chọn gốc tọa độ O tại trung điểm AB.
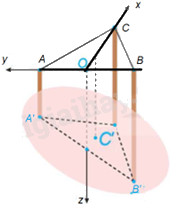
Khi đó, A(0;1;0) B(0;-1;0) C(\(\sqrt 3 \);0;0); A’(0;1;4); B’(0;-1;4,4); C’ (\(\sqrt 3 \);0; 4,8).
Ta có: \(\overrightarrow {A'B'} = \left( {0; - 2;0,4} \right);\overrightarrow {B'C'} = \left( {\sqrt 3 ;1;0,4} \right)\).
Mặt phẳng (A’B’C’) nhận \(\left[ {\overrightarrow {A'B'} ;\overrightarrow {B'C'} } \right]\) làm một vectơ pháp tuyến.
Ta có: \(\left[ {\overrightarrow {A'B'} ;\overrightarrow {B'C'} } \right] = \left( {\left| {\begin{array}{*{20}{c}}{ - 2}&{0,4}\\1&{0,4}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{0,4}&0\\{0,4}&{\sqrt 3 }\end{array}} \right|;\left| {\begin{array}{*{20}{c}}0&{ - 2}\\{\sqrt 3 }&1\end{array}} \right|} \right) = \left( {\frac{{ - 6}}{5};\frac{{2\sqrt 3 }}{5};2\sqrt 3 } \right)\).
Mặt phẳng đáy bể là mặt phẳng (A’ B’ C’) nên có vectơ pháp tuyến là \(\overrightarrow n = \left( { - \frac{6}{5};\frac{{2\sqrt 3 }}{5};2\sqrt 3 } \right)\).
Mặt phẳng ngang (mặt nước) là mặt phẳng (Oxy) có vectơ pháp tuyến là \(\overrightarrow k {\rm{ = }}\left( {0;0;1} \right)\).
Nên góc giữa mặt phẳng đáy bể và mặt phẳng ngang là:
\(\cos \left( {\left( {A'B'C'} \right),\left( {Oxy} \right)} \right) = \frac{{\left| {\frac{{ - 6}}{5}.0 + \frac{{2\sqrt 3 }}{5}.0 + 2\sqrt 3 .1} \right|}}{{\sqrt {{{\left( {\frac{{ - 6}}{5}} \right)}^2} + {{\left( {\frac{{2\sqrt 3 }}{5}} \right)}^2} + {{\left( {2\sqrt 3 } \right)}^2}} .\sqrt {{0^2} + {0^2} + {1^2}} }} = \frac{{5\sqrt {29} }}{{29}}\).
\( \Rightarrow \left( {\left( {A'B'C'} \right),\left( {Oxy} \right)} \right) \approx 21,{8^0}\).
Vậy đáy bể nghiêng so với mặt phẳng nằm ngang một góc khoảng 21,8 độ.
Bài tập 5.50 trang 63 SGK Toán 12 tập 2 - Kết nối tri thức thuộc chương trình học về tích phân. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về nguyên hàm, tích phân xác định để tính diện tích hình phẳng hoặc thể tích vật thể. Để giải bài tập này một cách hiệu quả, bạn cần nắm vững các khái niệm cơ bản và các công thức liên quan.
Để cung cấp lời giải chi tiết, chúng ta cần biết nội dung cụ thể của bài tập 5.50. Giả sử bài tập yêu cầu tính diện tích hình phẳng giới hạn bởi các đường y = f(x), y = g(x), x = a và x = b. Lời giải sẽ bao gồm các bước sau:
Giả sử bài tập 5.50 yêu cầu tính diện tích hình phẳng giới hạn bởi các đường y = x2, y = 4x và x = 0. Ta thực hiện các bước sau:
Vậy diện tích hình phẳng là 32/3.
Để củng cố kiến thức, bạn có thể tham khảo các bài tập tương tự trong SGK Toán 12 tập 2 - Kết nối tri thức hoặc trên các trang web học toán online khác.
Bài tập 5.50 trang 63 SGK Toán 12 tập 2 - Kết nối tri thức là một bài tập quan trọng giúp bạn rèn luyện kỹ năng vận dụng kiến thức về tích phân để giải quyết các bài toán thực tế. Hy vọng với lời giải chi tiết và các lưu ý trên, bạn sẽ giải bài tập này một cách dễ dàng và hiệu quả.