Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 12. Bài viết này sẽ hướng dẫn bạn giải bài tập 7 trang 90 SGK Toán 12 tập 2 - Kết nối tri thức một cách nhanh chóng và hiệu quả.
Chúng tôi cam kết mang đến cho bạn những giải pháp học tập tốt nhất, giúp bạn nắm vững kiến thức và đạt kết quả cao trong môn Toán.
Cho hàm số f(x) liên tục trên \(\mathbb{R}\). Gọi S là diện tích hình phẳng giới hạn bởi các đường \(y = f\left( x \right),y = 0,x = - 1\) và \(x = 4\) như hình bên. Khẳng định nào dưới đây là đúng? A. \(S = \int\limits_{ - 1}^1 {f\left( x \right)dx} + \int\limits_1^4 {f\left( x \right)dx} \). B. \(S = \int\limits_{ - 1}^1 {f\left( x \right)dx} - \int\limits_1^4 {f\left( x \right)dx} \). C. \(S = - \int\limits_{ - 1}^1 {f\left( x \right)dx} + \int\limits_1^4 {f\left( x \right)dx} \).
Đề bài
Cho hàm số f(x) liên tục trên \(\mathbb{R}\). Gọi S là diện tích hình phẳng giới hạn bởi các đường \(y = f\left( x \right),y = 0,x = - 1\) và \(x = 4\) như hình bên.
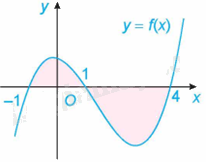
Khẳng định nào dưới đây là đúng?
A. \(S = \int\limits_{ - 1}^1 {f\left( x \right)dx} + \int\limits_1^4 {f\left( x \right)dx} \).
B. \(S = \int\limits_{ - 1}^1 {f\left( x \right)dx} - \int\limits_1^4 {f\left( x \right)dx} \).
C. \(S = - \int\limits_{ - 1}^1 {f\left( x \right)dx} + \int\limits_1^4 {f\left( x \right)dx} \).
D. \(S = - \int\limits_{ - 1}^1 {f\left( x \right)dx} - \int\limits_1^4 {f\left( x \right)dx} \).
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về diện tích hình phẳng giới hạn bởi hai đồ thị hàm số và đường thẳng \(x = a,x = b\) để tính: Diện tích S của hình phẳng giới hạn đồ thị của hai hàm số f(x), g(x) liên tục trên đoạn [a; b] và hai đường thẳng \(x = a,x = b\), được tính bằng công thức \(S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \).
Lời giải chi tiết
Diện tích hình phẳng cần tính là: \(S = \int\limits_{ - 1}^4 {\left| {f\left( x \right) - 0} \right|dx} = \int\limits_{ - 1}^1 {f\left( x \right)dx} - \int\limits_1^4 {f\left( x \right)dx} \)
Chọn B
Bài tập 7 trang 90 SGK Toán 12 tập 2 - Kết nối tri thức thuộc chương trình học về Đạo hàm. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức về đạo hàm của hàm số, đạo hàm của tổng, hiệu, tích, thương của các hàm số, và quy tắc đạo hàm của hàm hợp để giải quyết các bài toán cụ thể. Việc nắm vững các khái niệm và công thức đạo hàm là yếu tố then chốt để hoàn thành tốt bài tập này.
Bài tập 7 thường bao gồm các dạng bài sau:
Để giải quyết bài tập 7 trang 90 SGK Toán 12 tập 2 - Kết nối tri thức một cách hiệu quả, bạn có thể áp dụng các phương pháp sau:
Ví dụ: Tính đạo hàm của hàm số f(x) = x3 + 2x2 - 5x + 1.
Giải:
f'(x) = (x3)' + (2x2)' - (5x)' + (1)'
f'(x) = 3x2 + 4x - 5 + 0
f'(x) = 3x2 + 4x - 5
Khi giải bài tập 7 trang 90 SGK Toán 12 tập 2 - Kết nối tri thức, bạn cần lưu ý những điều sau:
Bài tập 7 trang 90 SGK Toán 12 tập 2 - Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm. Bằng cách áp dụng các phương pháp giải phù hợp và luyện tập thường xuyên, bạn có thể hoàn thành tốt bài tập này và đạt kết quả cao trong môn Toán.
| Hàm số | Đạo hàm |
|---|---|
| y = c (hằng số) | y' = 0 |
| y = xn | y' = nxn-1 |
| y = sinx | y' = cosx |
| y = cosx | y' = -sinx |