Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và chính xác các bài tập Toán 12 tập 1 - Kết nối tri thức. Bài viết này sẽ hướng dẫn bạn giải bài 1 trang 91 một cách dễ hiểu, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập hiệu quả nhất, đồng thời giúp bạn tiết kiệm thời gian và công sức.
Sử dụng phần mềm GeoGebra thực hiện các yêu cầu sau: Cho các hàm số đa thức sau: (1) (y = 3{x^2} + sqrt 3 x + 1); (2) (y = {x^3} - 6{x^2} + 9), (3) (y = {x^4} - 4{x^2} + 3). a) Tìm đạo hàm cấp một và đạo hàm cấp hai của các hàm số trên. b) Tìm tất cả các điểm cực trị của các hàm số trên. c) Vẽ đồ thị của các hàm số trên.
Đề bài
Sử dụng phần mềm GeoGebra thực hiện các yêu cầu sau:
Cho các hàm số đa thức sau:
(1) \(y = 3{x^2} + \sqrt 3 x + 1\); (2) \(y = {x^3} - 6{x^2} + 9\), (3) \(y = {x^4} - 4{x^2} + 3\).
a) Tìm đạo hàm cấp một và đạo hàm cấp hai của các hàm số trên.
b) Tìm tất cả các điểm cực trị của các hàm số trên.
c) Vẽ đồ thị của các hàm số trên.
Phương pháp giải - Xem chi tiết
a, b) Sử dụng kiến thức về các cú pháp lệnh trong GeoGebra để thực hiện:

c) Sử dụng kiến thức về vẽ đồ thị của hàm đa thức để vẽ đồ thị hàm số: Nhập hàm số vào ô lệnh, màn hình sẽ hiển thị đồ thị hàm số cần vẽ.
Lời giải chi tiết
a) Hàm số \(y = 3{x^2} + \sqrt 3 x + 1\)
Để tính đạo hàm cấp 1 ta nhập DaoHam (\(3{x^2} + \sqrt 3 x + 1\))
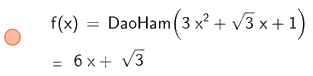
Do đó, đạo hàm cấp 1 của hàm số \(y = 3{x^2} + \sqrt 3 x + 1\) là \(6x + \sqrt 3 \)
Để tính đạo hàm cấp 2 ta nhập DaoHam (\(3{x^2} + \sqrt 3 x + 1\), 2)

Do đó, đạo hàm cấp 2 của hàm số \(y = 3{x^2} + \sqrt 3 x + 1\) là \(6\)
Hàm số \(y = {x^3} - 6{x^2} + 9\)
Để tính đạo hàm cấp 1 ta nhập DaoHam (\({x^3} - 6{x^2} + 9\))
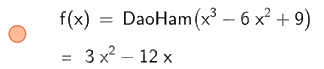
Do đó, đạo hàm cấp 1 của hàm số \(y = {x^3} - 6{x^2} + 9\) là \(3{x^2} - 12x\)
Để tính đạo hàm cấp 2 ta nhập DaoHam (, 2)
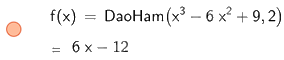
Do đó, đạo hàm cấp 2 của hàm số \(y = {x^3} - 6{x^2} + 9\) là \(6x - 12\)
Hàm số \(y = {x^4} - 4{x^2} + 3\)
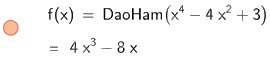
Để tính đạo hàm cấp 1 ta nhập DaoHam (\({x^4} - 4{x^2} + 3\))
Do đó, đạo hàm cấp 1 của hàm số \(y = {x^4} - 4{x^2} + 3\) là \(4{x^3} - 8x\)
Để tính đạo hàm cấp 2 ta nhập DaoHam (\({x^4} - 4{x^2} + 3\), 2)
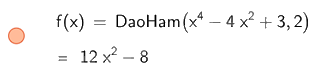
Do đó, đạo hàm cấp 2 của hàm số \(y = {x^4} - 4{x^2} + 3\) là \(12{x^2} - 8\)
b) Hàm số \(y = 3{x^2} + \sqrt 3 x + 1\)
Để tìm cực trị ta nhập lệnh, kết quả hiện thị ngay bên dưới:
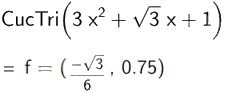
Do đó, hàm số \(y = 3{x^2} + \sqrt 3 x + 1\) có điểm cực trị là \(\left( {\frac{{ - \sqrt 3 }}{6};0,75} \right)\)
Hàm số \(y = {x^3} - 6{x^2} + 9\)
Để tìm cực trị ta nhập lệnh, kết quả hiện thị ngay bên dưới:
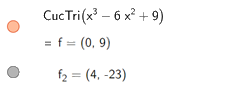
Do đó, hàm số \(y = {x^3} - 6{x^2} + 9\) có các điểm cực trị là \(\left( {0;9} \right);\left( {4; - 23} \right)\)
Hàm số \(y = {x^4} - 4{x^2} + 3\)
Để tìm cực trị ta nhập lệnh, kết quả hiện thị ngay bên dưới:
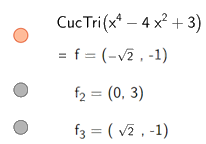
Do đó, hàm số \(y = {x^4} - 4{x^2} + 3\) có các điểm cực trị là \(\left( { - \sqrt 2 ; - 1} \right);\left( {0;3} \right);\left( {\sqrt 2 ; - 1} \right)\)
c) Đồ thị hàm số \(y = 3{x^2} + \sqrt 3 x + 1\): Ta nhập hàm số \(y = 3{x^2} + \sqrt 3 x + 1\) vào ô lệnh, màn hình sẽ hiển thị đồ thị của hàm số cần vẽ:
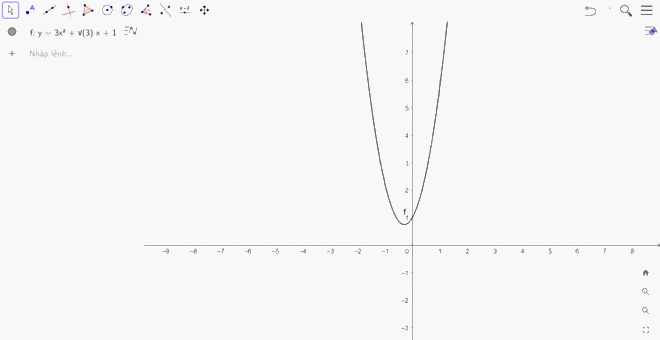
Đồ thị hàm số \(y = {x^3} - 6{x^2} + 9\): Ta nhập hàm số \(y = {x^3} - 6{x^2} + 9\) vào ô lệnh, màn hình sẽ hiển thị đồ thị của hàm số cần vẽ:
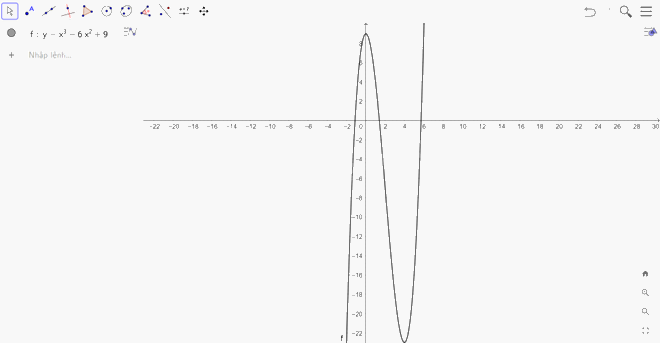
Đồ thị hàm số \(y = {x^4} - 4{x^2} + 3\): Ta nhập hàm số \(y = {x^4} - 4{x^2} + 3\) vào ô lệnh, màn hình sẽ hiển thị đồ thị của hàm số cần vẽ:
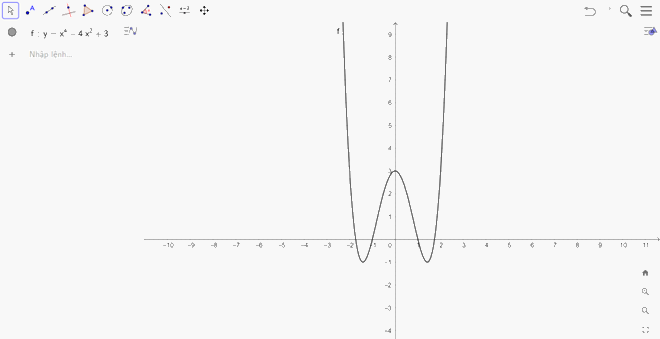
Bài 1 trang 91 SGK Toán 12 tập 1 - Kết nối tri thức thuộc chương trình học về giới hạn của hàm số. Bài tập này yêu cầu học sinh vận dụng kiến thức về định nghĩa giới hạn để tính giới hạn của hàm số tại một điểm. Việc nắm vững kiến thức này là nền tảng quan trọng để học các kiến thức tiếp theo về đạo hàm và tích phân.
Bài 1 trang 91 SGK Toán 12 tập 1 - Kết nối tri thức thường bao gồm các dạng bài tập sau:
Để giải bài 1 trang 91 SGK Toán 12 tập 1 - Kết nối tri thức, chúng ta cần thực hiện các bước sau:
Ví dụ, xét bài tập sau:
Tính limx→2 (x2 - 4) / (x - 2)
Lời giải:
Ta có:
limx→2 (x2 - 4) / (x - 2) = limx→2 (x - 2)(x + 2) / (x - 2) = limx→2 (x + 2) = 2 + 2 = 4
Ngoài bài 1 trang 91, SGK Toán 12 tập 1 - Kết nối tri thức còn có nhiều bài tập tương tự về giới hạn hàm số. Để giải các bài tập này, bạn có thể áp dụng các phương pháp sau:
Để học tốt môn Toán 12, bạn nên:
Dưới đây là một số tài liệu tham khảo hữu ích cho việc học Toán 12:
Bài 1 trang 91 SGK Toán 12 tập 1 - Kết nối tri thức là một bài tập quan trọng giúp bạn củng cố kiến thức về giới hạn hàm số. Hy vọng với lời giải chi tiết và các phương pháp giải bài tập tương tự mà chúng tôi đã cung cấp, bạn sẽ tự tin hơn trong quá trình học tập môn Toán 12.