Giải bài tập 2.2 trang 58 SGK Toán 12 tập 1 - Kết nối tri thức

Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 12. Bài viết này sẽ hướng dẫn bạn cách giải bài tập 2.2 trang 58 SGK Toán 12 tập 1 - Kết nối tri thức một cách nhanh chóng và hiệu quả.

Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn, đặc biệt là với những bài tập đòi hỏi sự tư duy logic và vận dụng kiến thức. Vì vậy, chúng tôi luôn cố gắng cung cấp những lời giải rõ ràng, chi tiết, kèm theo các giải thích cụ thể để bạn có thể hiểu rõ bản chất của bài toán.

Cho hình hộp chữ nhật ABCD.A’B’C’D’ có (AB = 2,AD = 3) và (AA' = 4). Tính độ dài của các vectơ (overrightarrow {BB'} ,overrightarrow {BD} ) và (overrightarrow {BD'} ).

Đề bài

Cho hình hộp chữ nhật ABCD.A’B’C’D’ có \(AB = 2,AD = 3\) và \(AA' = 4\). Tính độ dài của các vectơ \(\overrightarrow {BB'} ,\overrightarrow {BD} \) và \(\overrightarrow {BD'} \).

Phương pháp giải - Xem chi tiết Giải bài tập 2.2 trang 58 SGK Toán 12 tập 1 - Kết nối tri thức 1

Sử dụng kiến thức về độ dài vectơ để tính: Độ dài của vectơ trong không gian là khoảng cách giữa điểm đầu và điểm cuối của vectơ đó. Độ dài của vectơ \(\overrightarrow a \) được kí hiệu là \(\left| {\overrightarrow a } \right|\).

Lời giải chi tiết

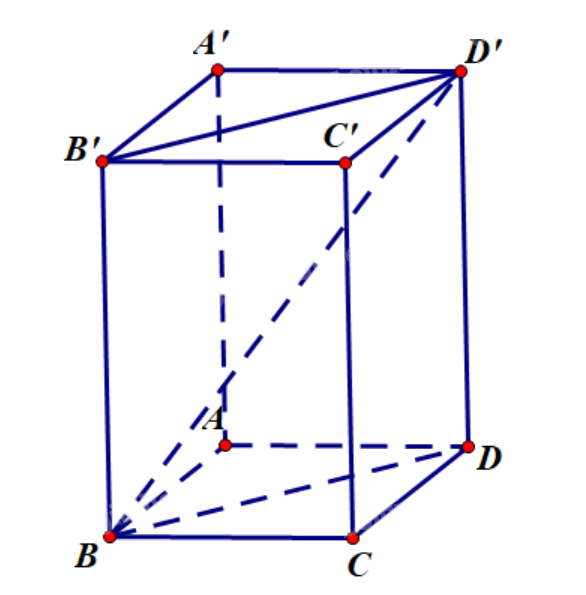
Giải bài tập 2.2 trang 58 SGK Toán 12 tập 1 - Kết nối tri thức 2

Vì B’BAA’ là hình chữ nhật nên \(BB' = AA' = DD' = 4 \Rightarrow \left| {\overrightarrow {BB'} } \right| = 4\).

Vì tứ giác ABCD là hình chữ nhật nên tam giác BAD vuông tại A.

Do đó, \(BD = \sqrt {A{B^2} + A{D^2}} = \sqrt {{2^2} + {3^2}} = \sqrt {13} \) (định lí Pythagore), suy ra: \(\left| {\overrightarrow {BD} } \right| = \sqrt {13} \).

Vì BB’D’D là hình chữ nhật nên tam giác DD’B vuông tại D.

Theo định lí Pythagore ta có: \(BD' = \sqrt {B{D^2} + DD{'^2}} = \sqrt {13 + {4^2}} = \sqrt {29} \Rightarrow \left| {\overrightarrow {BD'} } \right| = \sqrt {29} \).

Tự tin bứt phá Kỳ thi THPT Quốc gia môn Toán! Đừng bỏ lỡ Giải bài tập 2.2 trang 58 SGK Toán 12 tập 1 - Kết nối tri thức đặc sắc thuộc chuyên mục toán lớp 12 trên nền tảng toán học. Với bộ bài tập toán trung học phổ thông được biên soạn chuyên sâu, bám sát cấu trúc đề thi và chương trình Toán 12, đây chính là "chiến lược vàng" giúp các em tối ưu hóa ôn luyện. Học sinh sẽ không chỉ làm chủ mọi dạng bài thi mà còn nắm vững chiến thuật làm bài hiệu quả, sẵn sàng tự tin chinh phục điểm cao, vững bước vào đại học mơ ước nhờ phương pháp học trực quan, khoa học và hiệu quả học tập vượt trội!

Giải bài tập 2.2 trang 58 SGK Toán 12 tập 1 - Kết nối tri thức: Tổng quan

Bài tập 2.2 trang 58 SGK Toán 12 tập 1 - Kết nối tri thức thuộc chương trình học về giới hạn của hàm số. Bài tập này yêu cầu học sinh vận dụng kiến thức về định nghĩa giới hạn, các tính chất của giới hạn và các phương pháp tính giới hạn để giải quyết các bài toán cụ thể.

Nội dung bài tập 2.2

Bài tập 2.2 bao gồm một số câu hỏi nhỏ, yêu cầu học sinh tính giới hạn của các hàm số tại một điểm cho trước. Các hàm số có thể là hàm đa thức, hàm hữu tỉ, hoặc các hàm số phức tạp hơn. Để giải quyết bài tập này, học sinh cần nắm vững các kiến thức sau:

Định nghĩa giới hạn: Hiểu rõ khái niệm giới hạn của hàm số tại một điểm.
Các tính chất của giới hạn: Biết cách vận dụng các tính chất của giới hạn để đơn giản hóa bài toán.
Các phương pháp tính giới hạn: Nắm vững các phương pháp tính giới hạn như phương pháp trực tiếp, phương pháp phân tích thành nhân tử, phương pháp nhân liên hợp, và phương pháp sử dụng định lý L'Hopital.

Hướng dẫn giải chi tiết bài tập 2.2

Để giúp bạn hiểu rõ hơn về cách giải bài tập 2.2, chúng tôi sẽ trình bày lời giải chi tiết cho từng câu hỏi nhỏ:

Câu a: Tính lim_x→2 (x² - 4) / (x - 2)

Để tính giới hạn này, ta có thể phân tích tử số thành nhân tử:

(x² - 4) = (x - 2)(x + 2)

Khi đó, biểu thức trở thành:

lim_x→2 (x - 2)(x + 2) / (x - 2) = lim_x→2 (x + 2)

Thay x = 2 vào biểu thức, ta được:

lim_x→2 (x + 2) = 2 + 2 = 4

Vậy, lim_x→2 (x² - 4) / (x - 2) = 4

Câu b: Tính lim_x→0 sin(x) / x

Đây là một giới hạn quen thuộc trong toán học. Giới hạn này có thể được tính bằng định lý L'Hopital hoặc bằng cách sử dụng quy tắc giới hạn đặc biệt:

lim_x→0 sin(x) / x = 1

Câu c: Tính lim_x→∞ (2x + 1) / (x - 3)

Để tính giới hạn này, ta có thể chia cả tử số và mẫu số cho x:

lim_x→∞ (2x + 1) / (x - 3) = lim_x→∞ (2 + 1/x) / (1 - 3/x)

Khi x → ∞, 1/x → 0 và 3/x → 0. Do đó:

lim_x→∞ (2 + 1/x) / (1 - 3/x) = (2 + 0) / (1 - 0) = 2

Vậy, lim_x→∞ (2x + 1) / (x - 3) = 2

Lưu ý khi giải bài tập về giới hạn

Luôn kiểm tra xem giới hạn có tồn tại hay không trước khi tính toán.
Sử dụng các tính chất của giới hạn một cách hợp lý để đơn giản hóa bài toán.
Nắm vững các phương pháp tính giới hạn và lựa chọn phương pháp phù hợp cho từng bài toán cụ thể.
Kiểm tra lại kết quả sau khi tính toán để đảm bảo tính chính xác.

Kết luận

Bài tập 2.2 trang 58 SGK Toán 12 tập 1 - Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về giới hạn của hàm số. Hy vọng rằng với hướng dẫn chi tiết này, bạn đã có thể giải quyết bài tập này một cách dễ dàng và hiệu quả. Chúc bạn học tập tốt!