Chào mừng các em học sinh đến với lời giải chi tiết bài tập 1.40 trang 43 SGK Toán 12 tập 1 - Kết nối tri thức. Bài viết này sẽ cung cấp phương pháp giải bài tập một cách dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán, cung cấp các giải pháp học tập hiệu quả và chất lượng.
Xét chiều biến thiên và tìm các cực trị (nếu có) của các hàm số sau: a) (y = {x^3} - 3{x^2} + 3x - 1); b) (y = {x^4} - 2{x^2} - 1); c) (y = frac{{2x - 1}}{{3x + 1}}); d) (y = frac{{{x^2} + 2x + 2}}{{x + 1}}).
Đề bài
Xét chiều biến thiên và tìm các cực trị (nếu có) của các hàm số sau:a) \(y = {x^3} - 3{x^2} + 3x - 1\);b) \(y = {x^4} - 2{x^2} - 1\);c) \(y = \frac{{2x - 1}}{{3x + 1}}\);d) \(y = \frac{{{x^2} + 2x + 2}}{{x + 1}}\).
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về cách tìm cực trị của hàm số \(y = f\left( x \right)\) để tìm cực trị của hàm số:
1. Tìm tập xác định của hàm số.
2. Tính đạo hàm f’(x). Tìm các điểm mà tại đó đạo hàm f’(x) bằng 0 hoặc đạo hàm không tồn tại.
3. Lập bảng biến thiên của hàm số.
4. Từ bảng biến thiên suy ra các cực trị của hàm số.
Lời giải chi tiết
a) Tập xác định: \(D = \mathbb{R}\).
Ta có: \(y' = 3{x^2} - 6x + 3 = 3{\left( {x - 1} \right)^2},y' = 0 \Leftrightarrow x = 1\)
Lập bảng biến thiên của hàm số:
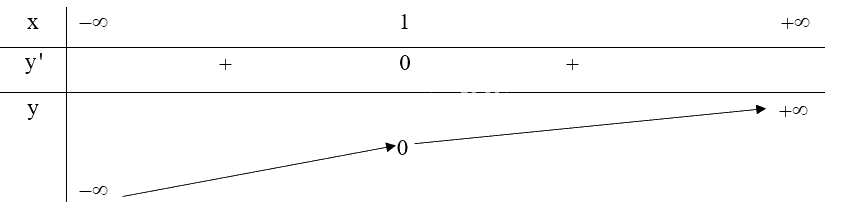
Hàm số \(y = {x^3} - 3{x^2} + 3x - 1\) đồng biến trên R.
Hàm số \(y = {x^3} - 3{x^2} + 3x - 1\) không có cực trị.
b) Tập xác định của hàm số là \(D = \mathbb{R}\).
Ta có: \(y' = 4{x^3} - 4x,y' = 0 \Leftrightarrow 4{x^3} - 4x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \pm 1\end{array} \right.\)
Bảng biến thiên:
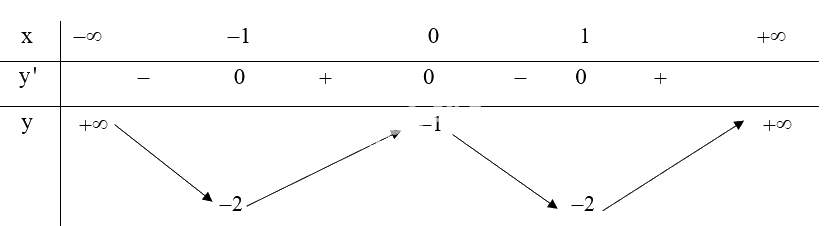
Từ bảng biến thiên ta có:
Hàm số \(y = {x^4} - 2{x^2} - 1\) đồng biến trên khoảng \(\left( { - 1;0} \right)\) và \(\left( {1; + \infty } \right)\).
Hàm số \(y = {x^4} - 2{x^2} - 1\) nghịch biến trên khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( {0;1} \right)\).
Hàm số \(y = {x^4} - 2{x^2} - 1\) đạt cực đại tại \(x = 0\) và .
Hàm số \(y = {x^4} - 2{x^2} - 1\) đạt cực tiểu tại \(x = \pm 1\) và \({y_{CT}} = - 2\).
c) Tập xác định: \(D = \mathbb{R}\backslash \left\{ { - \frac{1}{3}} \right\}\).
Ta có: \(y' = \frac{{2\left( {3x + 1} \right) - 3\left( {2x - 1} \right)}}{{{{\left( {3x + 1} \right)}^2}}} = \frac{5}{{{{\left( {3x + 1} \right)}^2}}} > 0\;\forall x \ne \frac{{ - 1}}{3}\)
Lập bảng biến thiên của hàm số:
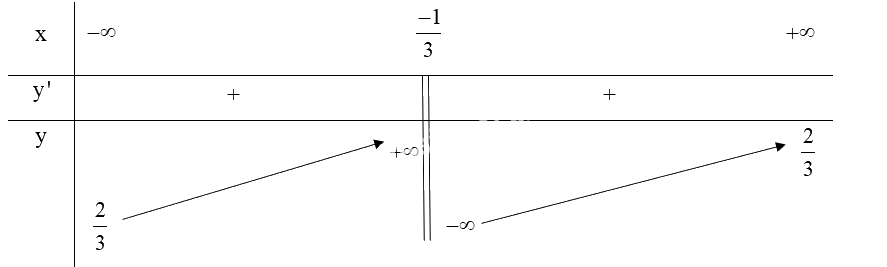
Từ bảng biến thiên ta có:
Hàm số \(y = \frac{{2x - 1}}{{3x + 1}}\) đồng biến trên \(\left( { - \infty ;\frac{{ - 1}}{3}} \right)\) và \(\left( {\frac{{ - 1}}{3}; + \infty } \right)\).
Hàm số không có cực trị.
d) Tập xác định: \(D = \mathbb{R}\backslash \left\{ { - 1} \right\}\).
Ta có: \(y' = \frac{{\left( {2x + 2} \right)\left( {x + 1} \right) - \left( {{x^2} + 2x + 2} \right)}}{{{{\left( {x + 1} \right)}^2}}} = \frac{{{x^2} + 2x}}{{{{\left( {x + 1} \right)}^2}}}\)
\(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = - 2\end{array} \right.\) (thỏa mãn)
Lập bảng biến thiên của hàm số:
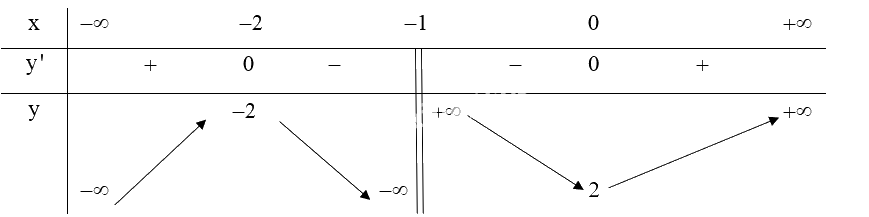
Từ bảng biến thiên ta có:
Hàm số \(y = \frac{{{x^2} + 2x + 2}}{{x + 1}}\) đồng biến trên khoảng \(\left( { - \infty ; - 2} \right)\) và \(\left( {0; + \infty } \right)\).
Hàm số \(y = \frac{{{x^2} + 2x + 2}}{{x + 1}}\) nghịch biến trên khoảng \(\left( { - 2; - 1} \right)\) và \(\left( { - 1;0} \right)\).
Hàm số \(y = \frac{{{x^2} + 2x + 2}}{{x + 1}}\) đạt cực đại tại \(x = - 2\) và \({y_{CĐ}} = -2\).
Hàm số \(y = \frac{{{x^2} + 2x + 2}}{{x + 1}}\) đạt cực tiểu tại \(x = 0\) và \({y_{CT}} = 2\).
Bài tập 1.40 trang 43 SGK Toán 12 tập 1 - Kết nối tri thức thuộc chương trình học về đạo hàm. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm của hàm số để giải quyết các bài toán thực tế. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các khái niệm và công thức liên quan đến đạo hàm, bao gồm:
Bài tập 1.40 thường có dạng yêu cầu tính đạo hàm của một hàm số tại một điểm hoặc trên một khoảng. Ngoài ra, bài tập có thể yêu cầu tìm điều kiện để hàm số có đạo hàm tại một điểm hoặc tìm các điểm không có đạo hàm. Để giải quyết các bài tập này, chúng ta cần thực hiện các bước sau:
(Giả sử bài tập 1.40 là: Tính đạo hàm của hàm số f(x) = x^3 - 2x^2 + x - 1)
Lời giải:
Để tính đạo hàm của hàm số f(x) = x^3 - 2x^2 + x - 1, ta áp dụng các quy tắc tính đạo hàm:
Vậy, f'(x) = 3x^2 - 4x + 1
Để hiểu rõ hơn về cách giải bài tập 1.40, chúng ta hãy xem xét một ví dụ minh họa khác:
(Giả sử bài tập là: Tìm đạo hàm của hàm số g(x) = sin(2x))
Lời giải:
Để tìm đạo hàm của hàm số g(x) = sin(2x), ta áp dụng quy tắc đạo hàm hợp:
(sin(u))' = cos(u) * u'
Trong trường hợp này, u = 2x, vậy u' = 2
Do đó, g'(x) = cos(2x) * 2 = 2cos(2x)
Khi giải bài tập về đạo hàm, các em cần lưu ý một số điểm sau:
Đạo hàm có rất nhiều ứng dụng trong thực tế, bao gồm:
Bài tập 1.40 trang 43 SGK Toán 12 tập 1 - Kết nối tri thức là một bài tập quan trọng giúp các em củng cố kiến thức về đạo hàm. Hy vọng rằng, với lời giải chi tiết và các ví dụ minh họa trong bài viết này, các em sẽ tự tin hơn trong quá trình học tập và giải quyết các bài toán liên quan đến đạo hàm.
Giaitoan.edu.vn sẽ tiếp tục đồng hành cùng các em trong quá trình học tập môn Toán. Chúc các em học tốt!