Giải bài tập 5.19 trang 49 SGK Toán 12 tập 2 - Kết nối tri thức

Bài tập 5.19 trang 49 SGK Toán 12 tập 2 thuộc chương trình học Toán 12 Kết nối tri thức. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế liên quan đến hàm số.

Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập 5.19, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.

Trên mặt đất phẳng, người ta dựng một cây cột thẳng cao 6m vuông góc với mặt đất, có chân cột đặt tại vị trí O trên mặt đất. Tại một thời điểm, dưới ánh nắng mặt trời, bóng của đỉnh cột dưới mặt đất cách chân cột 3m về hướng S60oE (hướng tạo với hướng nam góc \({60^o}\) và tạo với hướng đông góc \({30^o}\)) (H.5.32). Chọn hệ trục Oxyz có gốc tọa độ là O, tia Ox chỉ hướng nam, tia Oy chỉ hướng đông, tia Oz chứa cây cột, đơn vị đo là mét. Hãy viết phương trình đường thẳng chứa tia nắng mặt trời đi

Đề bài

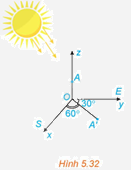
Trên mặt đất phẳng, người ta dựng một cây cột thẳng cao 6m vuông góc với mặt đất, có chân cột đặt tại vị trí O trên mặt đất. Tại một thời điểm, dưới ánh nắng mặt trời, bóng của đỉnh cột dưới mặt đất cách chân cột 3m về hướng S60^oE (hướng tạo với hướng nam góc \({60^o}\) và tạo với hướng đông góc \({30^o}\)) (H.5.32). Chọn hệ trục Oxyz có gốc tọa độ là O, tia Ox chỉ hướng nam, tia Oy chỉ hướng đông, tia Oz chứa cây cột, đơn vị đo là mét. Hãy viết phương trình đường thẳng chứa tia nắng mặt trời đi qua đỉnh cột tại thời điểm đang xét.

Giải bài tập 5.19 trang 49 SGK Toán 12 tập 2 - Kết nối tri thức 1

Phương pháp giải - Xem chi tiết Giải bài tập 5.19 trang 49 SGK Toán 12 tập 2 - Kết nối tri thức 2

Sử dụng kiến thức về lập phương trình đường thẳng đi qua hai điểm để viết phương trình: Trong không gian Oxyz, cho hai điểm phân biệt \({A_1}\left( {{x_1};{y_1};{z_1}} \right),{A_2}\left( {{x_2};{y_2};{z_2}} \right)\). Đường thẳng \({A_1}{A_2}\) có vectơ chỉ phương là \(\overrightarrow {{A_1}{A_2}} \left( {{x_2} - {x_1};{y_2} - {y_1};{z_2} - {z_1}} \right)\).

Đường thẳng \({A_1}{A_2}\) có phương trình đường thẳng tham số là: \(\left\{ \begin{array}{l}x = {x_1} + \left( {{x_2} - {x_1}} \right)t\\y = {y_1} + \left( {{y_2} - {y_1}} \right)t\\z = {z_1} + \left( {{z_2} - {z_1}} \right)t\end{array} \right.\left( {t \in \mathbb{R}} \right)\)

Sử dụng kiến thức về phương trình chính tắc của đường thẳng để viết phương trình đường thẳng: Trong không gian Oxyz, cho đường thẳng \(\Delta \) đi qua điểm \(A\left( {{x_0};{y_0};{z_0}} \right)\) và có vectơ chỉ phương \(\overrightarrow u = \left( {a;b;c} \right)\) với a, b, c là các số khác 0. Hệ phương trình \(\frac{{x - {x_0}}}{a} = \frac{{y - {y_0}}}{b} = \frac{{z - {z_0}}}{c}\) được gọi là phương trình chính tắc của đường thẳng \(\Delta \).

Lời giải chi tiết

Ta có: \(A\left( {0;0;6} \right),A'\left( {\frac{3}{2};\frac{{3\sqrt 3 }}{2};0} \right)\) nên \(\overrightarrow {AA'} \left( {\frac{3}{2};\frac{{3\sqrt 3 }}{2}; - 6} \right) \Rightarrow \frac{1}{3}\overrightarrow {AA'} = \left( {\frac{1}{2};\frac{{\sqrt 3 }}{2}; - 2} \right)\)

Đường thẳng AA’ đi qua điểm \(A\left( {0;0;6} \right)\) và nhận \(\frac{1}{3}\overrightarrow {AA'} = \left( {\frac{1}{2};\frac{{\sqrt 3 }}{2}; - 2} \right)\) làm vectơ chỉ phương nên phương trình tham số của đường thẳng AA’ là: \(\left\{ \begin{array}{l}x = \frac{1}{2}t\\y = \frac{{\sqrt 3 }}{2}t\\z = 6 - 2t\end{array} \right.\) và phương trình chính tắc là \(\frac{x}{{\frac{1}{2}}} = \frac{y}{{\frac{{\sqrt 3 }}{2}}} = \frac{{z - 6}}{{ - 2}} \Rightarrow \frac{{2x}}{1} = \frac{{2\sqrt 3 y}}{3} = \frac{{z - 6}}{{ - 2}}\).

Tự tin bứt phá Kỳ thi THPT Quốc gia môn Toán! Đừng bỏ lỡ Giải bài tập 5.19 trang 49 SGK Toán 12 tập 2 - Kết nối tri thức đặc sắc thuộc chuyên mục toán lớp 12 trên nền tảng soạn toán. Với bộ bài tập toán thpt được biên soạn chuyên sâu, bám sát cấu trúc đề thi và chương trình Toán 12, đây chính là "chiến lược vàng" giúp các em tối ưu hóa ôn luyện. Học sinh sẽ không chỉ làm chủ mọi dạng bài thi mà còn nắm vững chiến thuật làm bài hiệu quả, sẵn sàng tự tin chinh phục điểm cao, vững bước vào đại học mơ ước nhờ phương pháp học trực quan, khoa học và hiệu quả học tập vượt trội!

Giải bài tập 5.19 trang 49 SGK Toán 12 tập 2 - Kết nối tri thức: Đề bài

Bài tập 5.19 SGK Toán 12 tập 2 Kết nối tri thức yêu cầu học sinh giải một bài toán liên quan đến việc tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số sử dụng đạo hàm. Cụ thể, đề bài thường cho một hàm số và một khoảng xác định, yêu cầu tìm giá trị lớn nhất và nhỏ nhất của hàm số trên khoảng đó.

Phương pháp giải bài tập tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số

Tìm tập xác định của hàm số: Xác định miền giá trị mà hàm số có thể nhận.
Tính đạo hàm bậc nhất của hàm số: f'(x)
Tìm các điểm dừng của hàm số: Giải phương trình f'(x) = 0 để tìm các điểm mà đạo hàm bằng 0.
Xác định dấu của đạo hàm trên các khoảng xác định: Sử dụng bảng xét dấu để xác định khoảng hàm số đồng biến và nghịch biến.
Tính giá trị của hàm số tại các điểm dừng và các điểm mút của khoảng xác định: f(x₁), f(x₂), ...
So sánh các giá trị tìm được: Giá trị lớn nhất là giá trị lớn nhất trong các giá trị đã tính, giá trị nhỏ nhất là giá trị nhỏ nhất trong các giá trị đã tính.

Giải chi tiết bài tập 5.19 trang 49 SGK Toán 12 tập 2 - Kết nối tri thức

(Nội dung giải chi tiết bài tập 5.19 sẽ được trình bày tại đây. Bao gồm các bước thực hiện theo phương pháp đã nêu trên, với các phép tính cụ thể và giải thích rõ ràng. Ví dụ:)

Ví dụ: Giả sử hàm số f(x) = x³ - 3x + 2 trên khoảng [-2; 2].

Tập xác định: [-2; 2]
f'(x) = 3x² - 3
Giải f'(x) = 0: 3x² - 3 = 0 => x = ±1
Bảng xét dấu f'(x):

x	-∞	-1	1	+∞
f'(x)	+	-	+	+
f(x)	Đồng biến	Nghịch biến	Đồng biến	Đồng biến

Tính giá trị hàm số tại các điểm dừng và mút:

f(-2) = (-2)³ - 3(-2) + 2 = -8 + 6 + 2 = 0
f(-1) = (-1)³ - 3(-1) + 2 = -1 + 3 + 2 = 4
f(1) = (1)³ - 3(1) + 2 = 1 - 3 + 2 = 0
f(2) = (2)³ - 3(2) + 2 = 8 - 6 + 2 = 4

So sánh: Max f(x) = 4 tại x = -1 và x = 2; Min f(x) = 0 tại x = -2 và x = 1

Lưu ý khi giải bài tập

Luôn kiểm tra tập xác định của hàm số trước khi tính đạo hàm.
Chú ý các điểm không xác định của hàm số (ví dụ: mẫu số bằng 0).
Sử dụng bảng xét dấu đạo hàm để xác định khoảng hàm số đồng biến và nghịch biến một cách chính xác.
Kiểm tra lại các phép tính để tránh sai sót.

Ứng dụng của việc tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số

Việc tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số có nhiều ứng dụng trong thực tế, như:

Tối ưu hóa chi phí: Tìm giá trị nhỏ nhất của hàm chi phí để giảm thiểu chi phí sản xuất.
Tối đa hóa lợi nhuận: Tìm giá trị lớn nhất của hàm lợi nhuận để tăng lợi nhuận.
Thiết kế kỹ thuật: Tìm kích thước tối ưu của một vật thể để đạt được hiệu suất tốt nhất.

Hy vọng với lời giải chi tiết và phương pháp giải bài tập được trình bày trên, các em học sinh sẽ tự tin hơn khi giải các bài tập tương tự trong chương trình Toán 12 Kết nối tri thức.