Bài tập 2.28 trang 73 SGK Toán 12 tập 1 thuộc chương trình học Toán 12 Kết nối tri thức. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập 2.28, giúp các em học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Cho tứ diện đều ABCD có độ dài cạnh bằng a, gọi M là trung điểm của đoạn thẳng CD. Tích vô hướng \(\overrightarrow {AB} .\overrightarrow {AM} \) bằng A. \(\frac{{{a^2}}}{4}\). B. \(\frac{{{a^2}}}{2}\). C. \(\frac{{{a^2}}}{3}\). D. \({a^2}\).
Đề bài
Cho tứ diện đều ABCD có độ dài cạnh bằng a, gọi M là trung điểm của đoạn thẳng CD. Tích vô hướng \(\overrightarrow {AB} .\overrightarrow {AM} \) bằngA. \(\frac{{{a^2}}}{4}\).B. \(\frac{{{a^2}}}{2}\).C. \(\frac{{{a^2}}}{3}\).D. \({a^2}\).
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về công thức xác định tích vô hướng của hai vectơ trong không gian để tính: Trong không gian, cho hai vectơ \(\overrightarrow a \), \(\overrightarrow b \) đều khác \(\overrightarrow 0 \). Tích vô hướng của hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) là một số, kí hiệu là \(\overrightarrow a \cdot \overrightarrow b \), được xác định bởi công thức sau: \(\overrightarrow a \cdot \overrightarrow b = \left| {\overrightarrow a } \right| \cdot \left| {\overrightarrow b } \right| \cdot \cos \left( {\overrightarrow a ,\overrightarrow b } \right)\).
Lời giải chi tiết
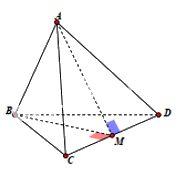
Tam giác ACD có ba cạnh bằng a nên tam giác ACD đều, AM là đường trung tuyến đồng thời là đường cao nên \(AM = \frac{{a\sqrt 3 }}{2}\).
Tam giác CBD có ba cạnh bằng a nên tam giác CBD đều, BM là đường trung tuyến đồng thời là đường cao nên \(BM = \frac{{a\sqrt 3 }}{2}\).
Áp dụng định côsin vào tam giác ABM ta có:
\(\cos \widehat {BAM} = \frac{{A{M^2} + A{B^2} - M{B^2}}}{{2AB.MB}} = \frac{{{{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2} + {a^2} - {{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2}}}{{2.\frac{{a\sqrt 3 }}{2}.a}} = \frac{{\sqrt 3 }}{3}\)
\(\overrightarrow {AB} .\overrightarrow {AM} = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AM} } \right|.\cos \left( {\overrightarrow {AB} ;\overrightarrow {AM} } \right) = a.\frac{{a\sqrt 3 }}{2}.\frac{{\sqrt 3 }}{3} = \frac{{{a^2}}}{2}\)
Chọn B
Bài tập 2.28 SGK Toán 12 tập 1 Kết nối tri thức là một bài toán ứng dụng đạo hàm để giải quyết một vấn đề thực tế. Để giải bài tập này, học sinh cần nắm vững các kiến thức về:
Dưới đây là lời giải chi tiết bài tập 2.28 trang 73 SGK Toán 12 tập 1 Kết nối tri thức:
Một vật thể chuyển động theo quy luật s = t3 - 3t2 + 5t + 2, trong đó s tính bằng mét và t tính bằng giây. Hãy tìm vận tốc của vật tại thời điểm t = 2.
Vận tốc của vật tại thời điểm t được tính bằng đạo hàm của hàm s theo t:
v(t) = s'(t) = 3t2 - 6t + 5
Thay t = 2 vào công thức trên, ta được:
v(2) = 3(2)2 - 6(2) + 5 = 12 - 12 + 5 = 5
Vậy vận tốc của vật tại thời điểm t = 2 là 5 m/s.
Bài toán này yêu cầu học sinh hiểu rõ mối liên hệ giữa quãng đường đi được (s) và vận tốc (v). Vận tốc là đạo hàm của quãng đường theo thời gian. Việc tính đạo hàm và thay giá trị t vào đạo hàm để tìm vận tốc là kỹ năng quan trọng trong chương trình Toán 12.
Để làm tốt các bài toán tương tự, học sinh cần:
Để củng cố kiến thức về đạo hàm và ứng dụng của đạo hàm, học sinh có thể tham khảo các bài tập sau:
Bài tập 2.28 trang 73 SGK Toán 12 tập 1 Kết nối tri thức là một bài toán ứng dụng đạo hàm đơn giản nhưng quan trọng. Việc giải bài tập này giúp học sinh hiểu rõ hơn về mối liên hệ giữa quãng đường, vận tốc và đạo hàm. Hy vọng với lời giải chi tiết và phân tích bài toán trên, các em học sinh sẽ nắm vững kiến thức và tự tin giải các bài tập tương tự.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán. Chúc các em học tập tốt!