Bài tập 3.4 trang 84 SGK Toán 12 tập 1 thuộc chương trình học Toán 12 Kết nối tri thức. Bài tập này thường xoay quanh các kiến thức về đạo hàm, ứng dụng của đạo hàm trong việc khảo sát hàm số và tìm cực trị.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập 3.4, giúp các em học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Kiểm tra khối lượng của 30 bao xi măng (đơn vị: kg) được chọn ngẫu nhiên trước khi xuất xưởng cho kết quả như sau: a) Thay dấu “?” bằng số thích hợp để hoàn thiện mẫu số liệu ghép nhóm sau. b) Tìm phương sai và độ lệch chuẩn của mẫu số liệu gốc và mẫu số liệu ghép nhóm. Giá trị nào là giá trị chính xác? Giá trị nào là giá trị xấp xỉ?
Đề bài
Kiểm tra khối lượng của 30 bao xi măng (đơn vị: kg) được chọn ngẫu nhiên trước khi xuất xưởng cho kết quả như sau:

a) Thay dấu “?” bằng số thích hợp để hoàn thiện mẫu số liệu ghép nhóm sau.

b) Tìm phương sai và độ lệch chuẩn của mẫu số liệu gốc và mẫu số liệu ghép nhóm. Giá trị nào là giá trị chính xác? Giá trị nào là giá trị xấp xỉ?
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về phương sai của mẫu số liệu ghép nhóm để tính: Phương sai của mẫu số liệu ghép nhóm, kí hiệu là \({s^2}\), là một số được tính theo công thức sau: \({s^2} = \frac{1}{n}\left( {{m_1}x_1^2 + ... + {m_k}x_k^2} \right) - {\left( {\overline x } \right)^2}\), trong đó \(n = {m_1} + ... + {m_k}\) với \(\overline x = \frac{{{m_1}{x_1} + ... + {m_k}{x_k}}}{n}\) là số trung bình của mẫu số liệu ghép nhóm.
Sử dụng kiến thức độ lệch chuẩn của mẫu số liệu ghép nhóm để tính: Độ lệch chuẩn của mẫu số liệu ghép nhóm, kí hiệu là s, là căn bậc hai số học của phương sai của mẫu số liệu ghép nhóm, tức là \(s = \sqrt {{s^2}} \)
Lời giải chi tiết
a) Hoàn thành bảng:

b) Với mẫu số liệu gốc:
+ Giá trị trung bình là: \(\overline x = (49,5 + 48,9 + 51,4 + 51,1 + 49,3 + 48,7 + 50,8 + 50,7 + 51,2 + \)
\( + 50,2 + 48,8 + 50,6 + 48,7 + 49,8 + 50,9 + 49,6 + 48,8 + 49,2 + 51,3 + 51,2 + 50,7 + 51,4 + \)
\( + 50,4 + 51,1 + 50,1 + 50,0 + 48,6 + 50,5 + 51,2 + 49,6).\frac{1}{{30}} = \frac{{15043}}{{300}}\)
+ Phương sai: 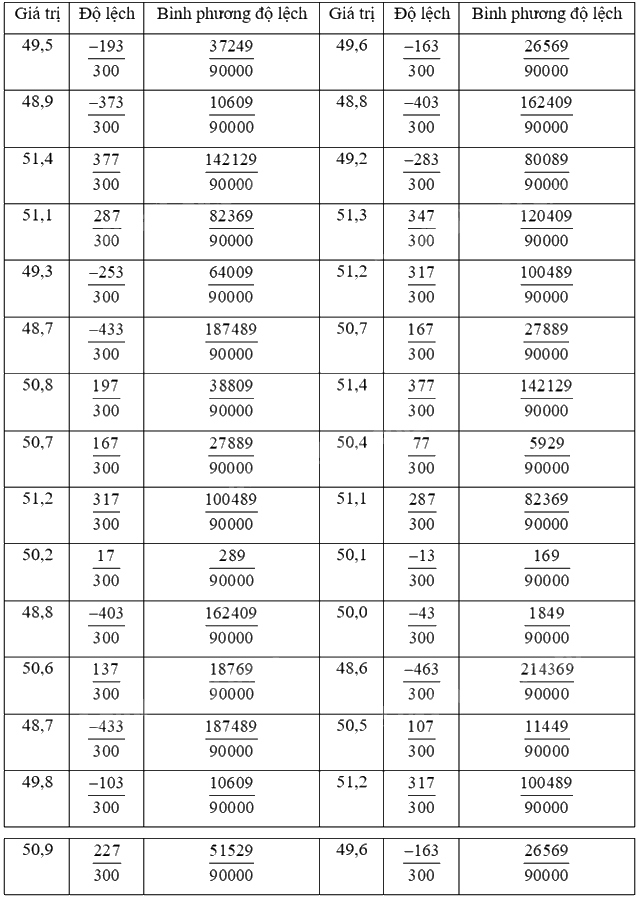
Tổng bình phương độ lệch: \(\frac{{78461}}{{3000}}\)
Phương sai: \({s^2} = \frac{1}{{30}}.\frac{{78461}}{{3000}} = \frac{{78461}}{{90000}}\)
Độ lệch chuẩn: \[s = \sqrt {{s^2}} = \frac{{\sqrt {78461} }}{{300}} \approx 0,934\]
Theo mẫu số liệu ghép nhóm:
Ta có bảng số liệu với giá trị đại diện:
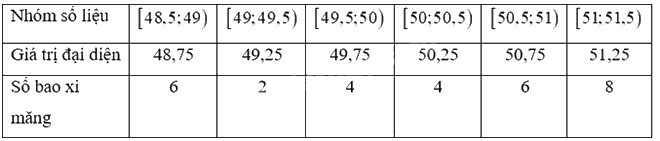
Giá trị trung bình: \(\overline x = \frac{{48,75.6 + 49,25.2 + 49,75.4 + 50,25.4 + 50,75.6 + 51,25.8}}{{30}} = \frac{{3011}}{{60}}\)
Phương sai:
\({s^2} = \frac{1}{{30}}\left( {48,{{75}^2}.6 + 49,{{25}^2}.2 + 49,{{75}^2}.4 + 50,{{25}^2}.4 + 50,{{75}^2}.6 + 51,{{25}^2}.8} \right) - {\left( {\frac{{3011}}{{60}}} \right)^2} = \frac{{194}}{{225}}\)
Độ lệch chuẩn: \(s = \sqrt {{s^2}} \approx 0,929\)
Giá trị tính từ mẫu số liệu gốc là chính xác, giá trị tính từ mẫu số liệu ghép nhóm là giá trị xấp xỉ.
Bài tập 3.4 trang 84 SGK Toán 12 tập 1 - Kết nối tri thức là một bài tập quan trọng trong chương trình học Toán 12, giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của đạo hàm. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm và định lý liên quan.
Đề bài thường yêu cầu học sinh thực hiện các thao tác sau:
Để giải bài tập 3.4 trang 84 SGK Toán 12 tập 1 - Kết nối tri thức, học sinh có thể áp dụng các phương pháp sau:
Ví dụ: Cho hàm số y = x3 - 3x2 + 2. Hãy khảo sát sự biến thiên và vẽ đồ thị của hàm số.
Lời giải:
Để giải bài tập 3.4 trang 84 SGK Toán 12 tập 1 - Kết nối tri thức một cách chính xác và hiệu quả, học sinh cần lưu ý những điều sau:
Bài tập 3.4 trang 84 SGK Toán 12 tập 1 - Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của đạo hàm. Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ giải bài tập một cách dễ dàng và hiệu quả.