Đường tiệm cận là một khái niệm quan trọng trong chương trình Toán 12, đặc biệt là khi nghiên cứu về đồ thị hàm số. Hiểu rõ lý thuyết đường tiệm cận giúp học sinh phân tích, vẽ và dự đoán được hình dạng của đồ thị hàm số một cách chính xác.
Tại giaitoan.edu.vn, chúng tôi cung cấp bài học chi tiết, dễ hiểu về lý thuyết đường tiệm cận, kèm theo các ví dụ minh họa và bài tập thực hành để bạn có thể nắm vững kiến thức một cách hiệu quả.
1. Đường tiệm cận ngang
1. Đường tiệm cận ngang
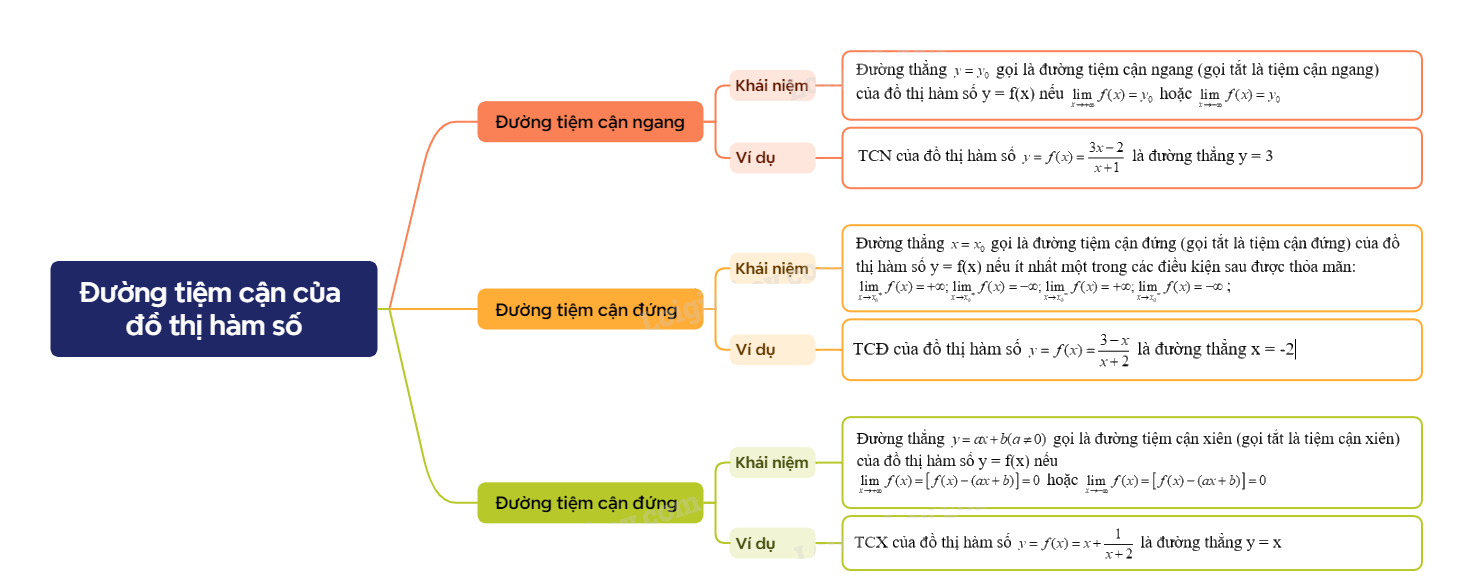
Đường thẳng \(y = {y_0}\) gọi là đường tiệm cận ngang (gọi tắt là tiệm cận ngang) của đồ thị hàm số y = f(x) nếu \(\mathop {\lim }\limits_{x \to + \infty } f(x) = {y_0}\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } f(x) = {y_0}\) |
Ví dụ: Tìm TCN của đồ thị hàm số \(y = f(x) = \frac{{3x - 2}}{{x + 1}}\)
Ta có: \(\mathop {\lim }\limits_{x \to + \infty } \frac{{3x - 2}}{{x + 1}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{3x - 2}}{{x + 1}} = 3\)
Vậy đồ thị hàm số f(x) có TCN là y = 3.
2. Đường tiệm cận đứng
Đường thẳng \(x = {x_0}\) gọi là đường tiệm cận đứng (gọi tắt là tiệm cận đứng) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn:\(\mathop {\lim }\limits_{x \to {x_0}^ + } f(x) = + \infty ;\mathop {\lim }\limits_{x \to {x_0}^ + } f(x) = - \infty ;\mathop {\lim }\limits_{x \to {x_0}^ - } f(x) = + \infty ;\mathop {\lim }\limits_{x \to {x_0}^ - } f(x) = - \infty \); |
Ví dụ: Tìm TCĐ của đồ thị hàm số \(y = f(x) = \frac{{3 - x}}{{x + 2}}\)
Ta có: \(\mathop {\lim }\limits_{x \to - {2^ + }} \frac{{3 - x}}{{x + 2}} = + \infty \)
Vậy đồ thị hàm số có TCĐ là x = -2
3.Đường tiệm cận xiên
Đường thẳng \(y = ax + b(a \ne 0)\) gọi là đường tiệm cận xiên (gọi tắt là tiệm cận xiên) của đồ thị hàm số y = f(x) nếu \(\mathop {\lim }\limits_{x \to + \infty } f(x) = \left[ {f(x) - (ax + b)} \right] = 0\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } f(x) = \left[ {f(x) - (ax + b)} \right] = 0\) |
Ví dụ: Tìm TCX của đồ thị hàm số \(y = f(x) = x + \frac{1}{{x + 2}}\)
Ta có: \(\mathop {\lim }\limits_{x \to + \infty } \left[ {f(x) - x} \right] = \mathop {\lim }\limits_{x \to + \infty } \frac{1}{{x + 2}} = 0\)
Vậy đồ thị hàm số có TCX là y = x
Đường tiệm cận đóng vai trò then chốt trong việc xác định hình dạng và tính chất của đồ thị hàm số. Việc nắm vững lý thuyết này không chỉ giúp học sinh giải quyết các bài toán trắc nghiệm và tự luận mà còn là nền tảng cho việc học tập các môn học liên quan đến toán học ở các cấp độ cao hơn.
Đường tiệm cận của đồ thị hàm số y = f(x) là đường thẳng mà đồ thị của hàm số tiến gần đến khi x hoặc y tiến đến vô cùng.
Việc tìm đường tiệm cận phụ thuộc vào dạng hàm số. Dưới đây là hướng dẫn tìm đường tiệm cận cho một số dạng hàm số thường gặp:
Xét hàm số y = P(x) / Q(x), trong đó P(x) và Q(x) là các đa thức.
Đối với hàm số mũ y = ax, đường tiệm cận ngang là y = 0. Đối với hàm số logarit y = logax, đường tiệm cận đứng là x = 0.
Ví dụ 1: Tìm đường tiệm cận của hàm số y = (2x + 1) / (x - 3).
Giải:
Ví dụ 2: Tìm đường tiệm cận của hàm số y = x2 + 1 / x.
Giải:
Để củng cố kiến thức về lý thuyết đường tiệm cận, bạn có thể thực hành giải các bài tập sau:
Hy vọng với những kiến thức và ví dụ trên, bạn đã nắm vững lý thuyết đường tiệm cận của đồ thị hàm số Toán 12 Kết nối tri thức. Chúc bạn học tập tốt!