Bài tập 1.22 trang 32 SGK Toán 12 tập 1 thuộc chương trình học Toán 12 Kết nối tri thức. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập 1.22 trang 32 SGK Toán 12 tập 1, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau: a) \(y = \frac{{2x + 1}}{{x + 1}}\); b) \(y = \frac{{x + 3}}{{1 - x}}\).
Đề bài
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau:
a) \(y = \frac{{2x + 1}}{{x + 1}}\);
b) \(y = \frac{{x + 3}}{{1 - x}}\).
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về sơ đồ khảo sát hàm số phân thức để khảo sát và vẽ đồ thị hàm số:
Sơ đồ khảo sát hàm số phân thức
1. Tìm tập xác định của hàm số.
2. Khảo sát sự biến thiên của hàm số:
+ Tính đạo hàm y’. Tìm các điểm tại đó y’ bằng 0 hoặc đạo hàm không tồn tại.
+ Xét dấu y’ để chỉ ra các khoảng đơn điệu của hàm số.
+ Tìm cực trị của hàm số.
+ Tìm các giới hạn tại vô cực, giới hạn vô cực và tìm tiệm cận của đồ thị hàm số.
+ Lập bảng biến thiên của hàm số.
3. Vẽ đồ thị của hàm số dựa vào bảng biến thiên.
Lời giải chi tiết
a) 1. Tập xác định của hàm số: \(\mathbb{R}\backslash \left\{ { - 1} \right\}\)
2. Sự biến thiên:
\(y' = \frac{1}{{{{\left( {x + 1} \right)}^2}}} > 0\forall x \ne - 1\)
Hàm số đồng biến trên khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( { - 1; + \infty } \right)\).
Hàm số không có cực trị.
\(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \frac{{2x + 1}}{{x + 1}} = 2;\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \frac{{2x + 1}}{{x + 1}} = 2\). \(\mathop {\lim }\limits_{x \to - {1^ - }} y = \mathop {\lim }\limits_{x \to - {1^ - }} \frac{{2x + 1}}{{x + 1}} = + \infty ;\mathop {\lim }\limits_{x \to - {1^ + }} y = \mathop {\lim }\limits_{x \to - {1^ + }} \frac{{2x + 1}}{{x + 1}} = - \infty \).
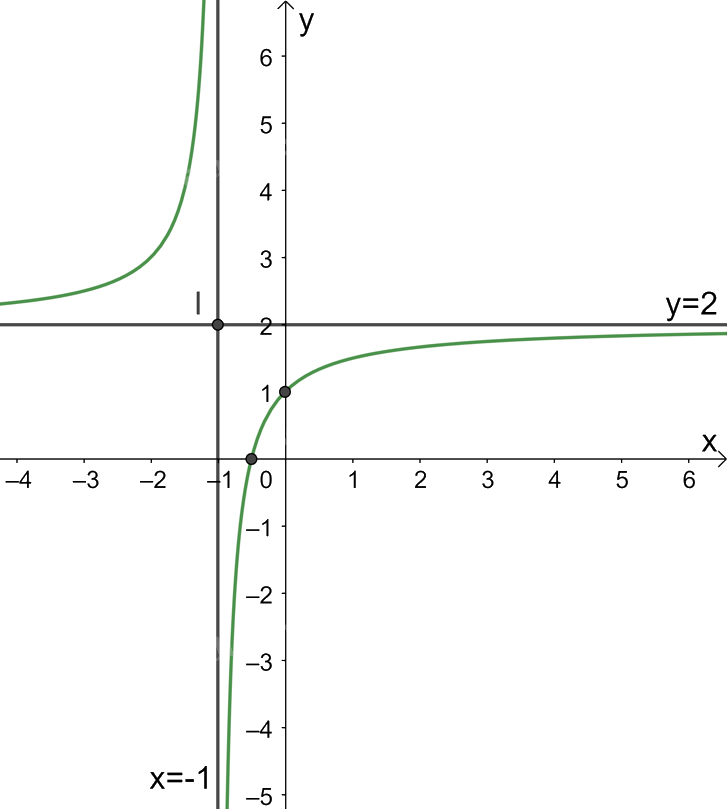
Do đó, đồ thị hàm số nhận đường thẳng \(x = - 1\) làm tiệm cận đứng và đường thẳng \(y = 2\) làm tiệm cận ngang.
Bảng biến thiên:

3. Đồ thị: Giao điểm của đồ thị hàm số với trục tung là (0;1).
\(y = 0 \Leftrightarrow \frac{{2x + 1}}{{x + 1}} = 0 \Leftrightarrow x = \frac{{ - 1}}{2}\)
Giao điểm của đồ thị hàm số với trục hoành là điểm \(\left( {\frac{{ - 1}}{2};0} \right)\).
Đồ thị hàm số nhận giao điểm I(-1; 2) của hai đường tiệm cận làm tâm đối xứng và nhận hai đường phân giác của góc tạo bởi hai đường tiệm cận này làm các trục đối xứng.
b) 1. Tập xác định của hàm số: \(\mathbb{R}\backslash \left\{ 1 \right\}\)
2. Sự biến thiên:
\(y' = \frac{4}{{{{\left( {1 - x} \right)}^2}}} > 0\forall x \ne 1\)
Hàm số đồng biến trên khoảng \(\left( { - \infty ;1} \right)\) và \(\left( {1; + \infty } \right)\).
Hàm số không có cực trị.
\(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \frac{{x + 3}}{{1 - x}} = - 1;\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \frac{{x + 3}}{{1 - x}} = - 1\) \(\mathop {\lim }\limits_{x \to {1^ - }} y = \mathop {\lim }\limits_{x \to {1^ - }} \frac{{x + 3}}{{1 - x}} = + \infty ;\mathop {\lim }\limits_{x \to {1^ + }} y = \mathop {\lim }\limits_{x \to {1^ + }} \frac{{x + 3}}{{1 - x}} = - \infty \)
Do đó, đồ thị hàm số nhận đường thẳng \(x = 1\) làm tiệm cận đứng và đường thẳng \(y = - 1\) làm tiệm cận ngang.
Bảng biến thiên:

3. Đồ thị:
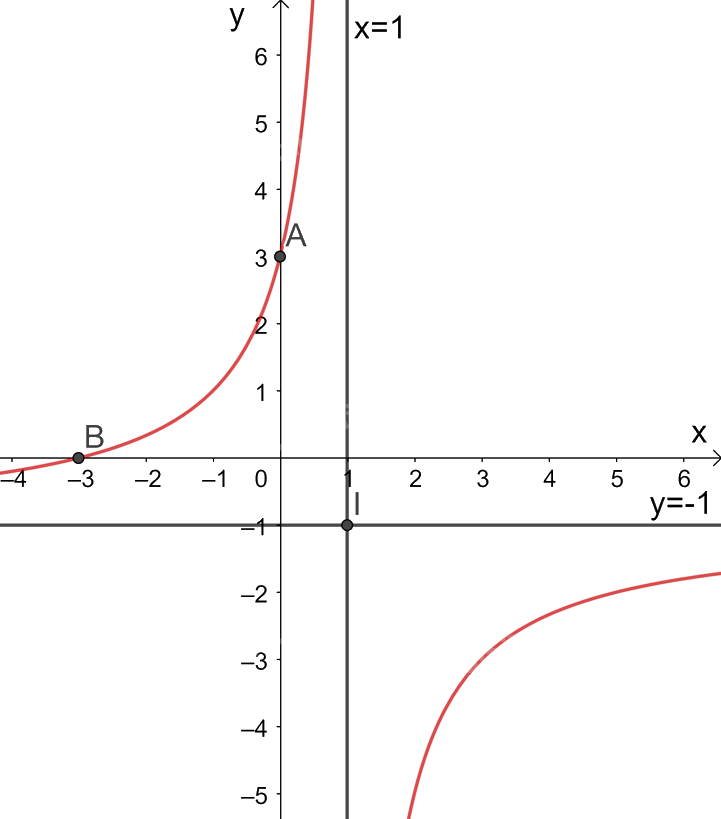
Giao điểm của đồ thị hàm số với trục tung là (0; 3).
\(y = 0 \Leftrightarrow \frac{{x + 3}}{{1 - x}} = 0 \Leftrightarrow x = - 3\)
Giao điểm của đồ thị hàm số với trục hoành là điểm \(\left( { - 3;0} \right)\).
Đồ thị hàm số nhận giao điểm I(1; -1) của hai đường tiệm cận làm tâm đối xứng và nhận hai đường phân giác của góc tạo bởi hai đường tiệm cận này làm các trục đối xứng.
Bài tập 1.22 trang 32 SGK Toán 12 tập 1 - Kết nối tri thức là một bài toán quan trọng trong chương trình học, giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của đạo hàm trong việc giải quyết các bài toán thực tế. Dưới đây là hướng dẫn giải chi tiết bài tập này:
Cho hàm số f(x) = x3 - 3x2 + 2. Tìm các điểm cực trị của hàm số.
f'(x) = 3x2 - 6x
f'(x) = 0 ⇔ 3x2 - 6x = 0 ⇔ 3x(x - 2) = 0
Vậy, x = 0 hoặc x = 2
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| f'(x) | + | - | + | |
| f(x) | NB | ĐC | NT |
(NB: Nghịch biến, ĐC: Đồng biến, NT: Ngược biến)
Đạo hàm có rất nhiều ứng dụng trong thực tế, ví dụ như:
Để nắm vững kiến thức về đạo hàm và ứng dụng của đạo hàm, các em nên luyện tập thêm các bài tập tương tự trong SGK và các tài liệu tham khảo khác. Giaitoan.edu.vn sẽ tiếp tục cung cấp các bài giải chi tiết và hướng dẫn giải các bài tập Toán 12 khác. Chúc các em học tốt!