Khoảng biến thiên và khoảng tứ phân vị là những khái niệm quan trọng trong thống kê, giúp đo lường mức độ phân tán của một tập dữ liệu. Trong chương trình Toán 12 Kết nối tri thức, việc nắm vững lý thuyết này là nền tảng để giải quyết các bài toán thực tế và nâng cao kỹ năng phân tích dữ liệu.
Giaitoan.edu.vn cung cấp bài giảng chi tiết, dễ hiểu cùng với các bài tập vận dụng đa dạng, giúp bạn tự tin chinh phục kiến thức về khoảng biến thiên và khoảng tứ phân vị.
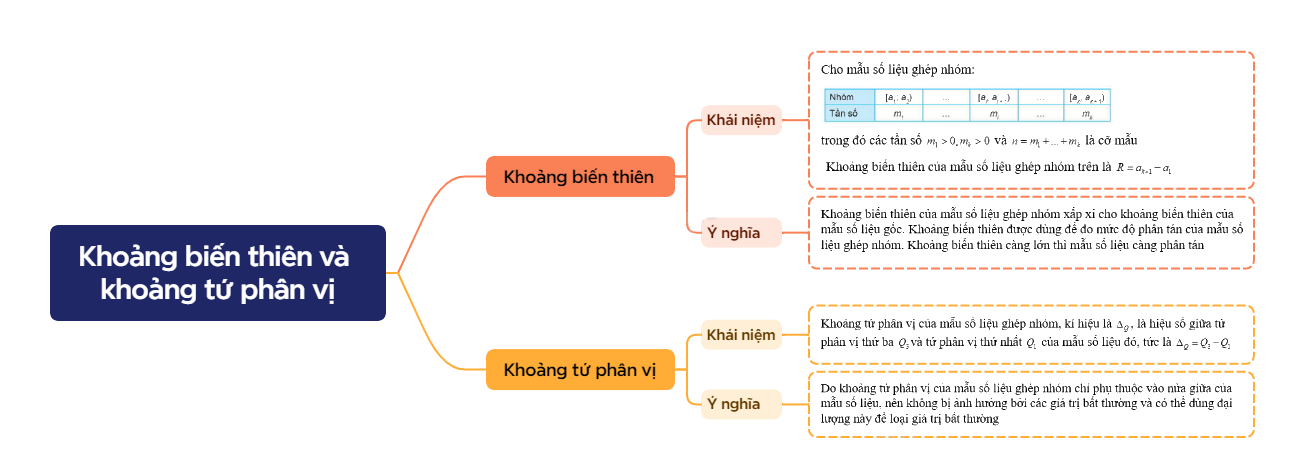
1. Khoảng biến thiên
1. Khoảng biến thiên
Cho mẫu số liệu ghép nhóm:

trong đó các tần số \({m_1} > 0,{m_k} > 0\) và \(n = {m_1} + ... + {m_k}\) là cỡ mẫu
Khoảng biến thiên của mẫu số liệu ghép nhóm trên là \(R = {a_{k + 1}} - {a_1}\) |
Ý nghĩa: Khoảng biến thiên của mẫu số liệu ghép nhóm xấp xỉ cho khoảng biến thiên của mẫu số liệu gốc. Khoảng biến thiên được dùng để đo mức độ phân tán của mẫu số liệu ghép nhóm. Khoảng biến thiên càng lớn thì mẫu số liệu càng phân tán
2. Khoảng tứ phân vị
Khoảng tứ phân vị của mẫu số liệu ghép nhóm, kí hiệu là \({\Delta _Q}\), là hiệu số giữa tứ phân vị thứ ba \({Q_3}\)và tứ phân vị thứ nhất \({Q_1}\) của mẫu số liệu đó, tức là \({\Delta _Q} = {Q_3} - {Q_1}\) |
Ý nghĩa: Do khoảng tứ phân vị của mẫu số liệu ghép nhóm chỉ phụ thuộc vào nửa giữa của mẫu số liệu, nên không bị ảnh hưởng bởi các giá trị bất thường và có thể dùng đại lượng này để loại giá trị bất thường
Trong chương trình Toán 12 Kết nối tri thức, thống kê đóng vai trò quan trọng trong việc phân tích và hiểu dữ liệu. Hai khái niệm then chốt trong phần này là khoảng biến thiên và khoảng tứ phân vị. Bài viết này sẽ cung cấp một cái nhìn toàn diện về lý thuyết, công thức và ứng dụng của chúng.
Khoảng biến thiên là một thước đo đơn giản để đánh giá mức độ phân tán của một tập dữ liệu. Nó được tính bằng hiệu giữa giá trị lớn nhất và giá trị nhỏ nhất trong tập dữ liệu đó.
Công thức:
R = Xmax - Xmin
Trong đó:
Ví dụ: Cho tập dữ liệu: 2, 5, 8, 11, 15. Khoảng biến thiên là 15 - 2 = 13.
Khoảng tứ phân vị là khoảng cách giữa tứ phân vị thứ nhất (Q1) và tứ phân vị thứ ba (Q3). Nó thể hiện phạm vi chứa 50% dữ liệu trung tâm của tập dữ liệu, ít bị ảnh hưởng bởi các giá trị ngoại lệ hơn so với khoảng biến thiên.
Các bước tính khoảng tứ phân vị:
Ví dụ: Cho tập dữ liệu: 3, 7, 8, 10, 12, 15, 18, 20.
| Đặc điểm | Khoảng biến thiên | Khoảng tứ phân vị |
|---|---|---|
| Cách tính | Xmax - Xmin | Q3 - Q1 |
| Ảnh hưởng bởi giá trị ngoại lệ | Cao | Thấp |
| Phạm vi dữ liệu | Toàn bộ dữ liệu | 50% dữ liệu trung tâm |
| Ứng dụng | Đánh giá nhanh mức độ phân tán | Đánh giá mức độ phân tán ổn định hơn |
Khoảng biến thiên và khoảng tứ phân vị được sử dụng rộng rãi trong nhiều lĩnh vực, bao gồm:
Bài 1: Tính khoảng biến thiên và khoảng tứ phân vị cho tập dữ liệu sau: 12, 15, 18, 20, 22, 25, 28.
Bài 2: So sánh khoảng biến thiên và khoảng tứ phân vị của hai tập dữ liệu sau và rút ra kết luận về mức độ phân tán của chúng:
Tập dữ liệu 1: 5, 10, 15, 20, 25
Tập dữ liệu 2: 5, 10, 15, 20, 100
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cơ bản và hữu ích về lý thuyết Khoảng biến thiên và khoảng tứ phân vị Toán 12 Kết nối tri thức. Hãy luyện tập thêm các bài tập để nắm vững kiến thức và áp dụng vào giải quyết các bài toán thực tế.