Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 12. Bài viết này sẽ hướng dẫn bạn cách giải bài tập 1.10 trang 19 SGK Toán 12 tập 1 - Kết nối tri thức một cách nhanh chóng và hiệu quả.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp bạn nắm vững kiến thức và đạt kết quả cao trong môn Toán.
Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau: a) (y = - {x^2} + 4x + 3); b) (y = {x^3} - 2{x^2} + 1) trên (left[ {0; + infty } right)); c) (y = frac{{{x^2} - 2x + 3}}{{x - 1}}) trên (left( {1; + infty } right)); d) (y = sqrt {4x - 2{x^2}} ).
Đề bài
Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau:a) \(y = - {x^2} + 4x + 3\);b) \(y = {x^3} - 2{x^2} + 1\) trên \(\left[ {0; + \infty } \right)\);c) \(y = \frac{{{x^2} - 2x + 3}}{{x - 1}}\) trên \(\left( {1; + \infty } \right)\);d) \(y = \sqrt {4x - 2{x^2}} \).
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về cách tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên một đoạn để tính: Giả sử \(y = f\left( x \right)\) là hàm số liên tục trên \(\left[ {a;b} \right]\) và có đạo hàm trên (a; b), có thể trừ ra tại một số hữu hạn điểm mà tại đó hàm số không có đạo hàm. Giả sử chỉ có hữu hạn điểm trong đoạn \(\left[ {a;b} \right]\) mà đạo hàm \(f'\left( x \right) = 0\).
Các bước tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn \(\left[ {a;b} \right]\):
1. Tìm các điểm \({x_1},{x_2},...{x_n} \in \left( {a;b} \right)\), tại đó \(f'\left( x \right) = 0\) hoặc không tồn tại.
2. Tính \(f\left( {{x_1}} \right);f\left( {{x_2}} \right);...;f\left( {{x_n}} \right)\), f(a) và f(b).
3. Tìm số lớn nhất M và số nhỏ nhất m trong các số trên. Ta có:
\(M = \mathop {\max }\limits_{\left[ {a;b} \right]} f\left( x \right),m = \mathop {\min }\limits_{\left[ {a;b} \right]} f\left( x \right)\)
Lời giải chi tiết
a) Ta có: \(y = - {x^2} + 4x + 3 \), khi đó \(y' = - 2x + 4 = 0 \Leftrightarrow x = 2\).
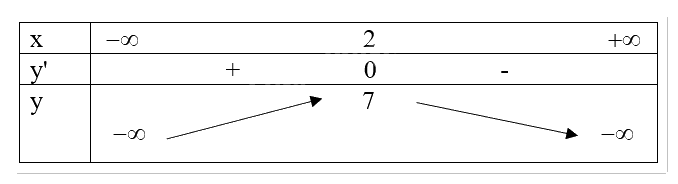
Do đó, \(\max f\left( x \right) = f\left( 2 \right) = 7\), hàm số không có giá trị nhỏ nhất.
b) GTLN, GTNN của \(y = {x^3} - 2{x^2} + 1\) trên \(\left[ {0; + \infty } \right)\).
Ta có: \(y' = 3{x^2} - 4x,y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\left( {tm} \right)\\x = \frac{4}{3}\left( {tm} \right)\end{array} \right.\)
Bảng biến thiên:
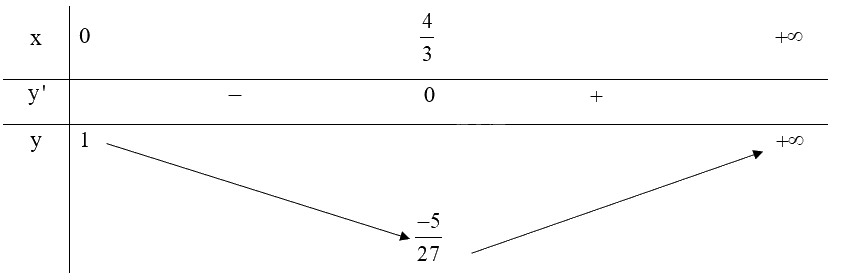
Do đó, \(\mathop {\min }\limits_{\left[ {0; + \infty } \right)} y = y\left( {\frac{4}{3}} \right) = \frac{{ - 5}}{{27}}\), hàm số không có giá trị lớn nhất.
c) Ta có: \(y' = \frac{{\left( {2x - 2} \right)\left( {x - 1} \right) - \left( {{x^2} - 2x + 3} \right)}}{{{{\left( {x - 1} \right)}^2}}} = \frac{{{x^2} - 2x - 1}}{{{{\left( {x - 1} \right)}^2}}}\)
\(y' = 0 \Leftrightarrow x = 1 + \sqrt 2 \) (do \(x \in \left( {1; + \infty } \right)\))
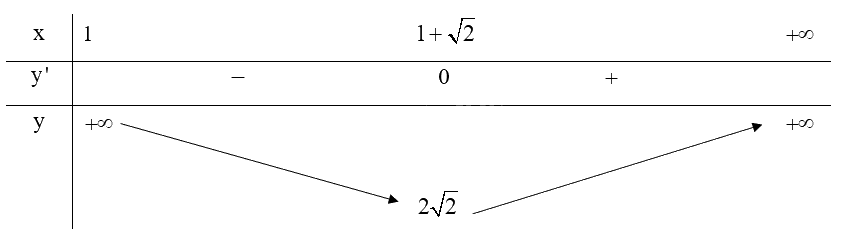
Do đó, \(\mathop {\min }\limits_{\left( {1; + \infty } \right)} y = y\left( {1 + \sqrt 2 } \right) = 2\sqrt 2 \), hàm số không có giá trị lớn nhất trên \(\left( {1; + \infty } \right)\).
d) Tập xác định của hàm số là: \(D = \left[ {0;2} \right]\)
\(y' = \frac{{\left( {4x - 2{x^2}} \right)'}}{{2\sqrt {4x - 2{x^2}} }} = \frac{{4 - 4x}}{{2\sqrt {4x - 2{x^2}} }} = \frac{{2\left( {1 - x} \right)}}{{\sqrt {4x - 2{x^2}} }}\)
\(y' = 0 \Leftrightarrow x = 1\left( {tm} \right)\)
\(y\left( 0 \right) = 0;y\left( 1 \right) = \sqrt 2 ;y\left( 2 \right) = 0\).
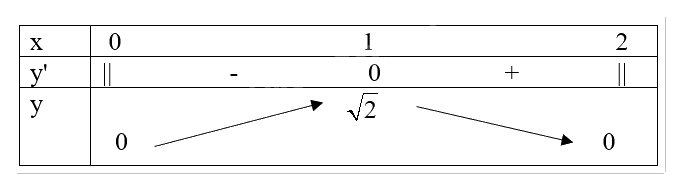
Do đó, \(\mathop {\max }\limits_{\left[ {0;2} \right]} y = y\left( 1 \right) = \sqrt 2 ,\mathop {\min }\limits_{\left[ {0;2} \right]} y = y\left( 0 \right) = y\left( 2 \right) = 0\).
Bài tập 1.10 trang 19 SGK Toán 12 tập 1 - Kết nối tri thức thuộc chương 1: Hàm số và đồ thị. Bài tập này yêu cầu học sinh vận dụng kiến thức về điều kiện xác định của hàm số, các phép toán trên hàm số và cách biểu diễn hàm số bằng đồ thị để giải quyết các bài toán cụ thể.
Bài tập 1.10 bao gồm các câu hỏi trắc nghiệm và bài tập tự luận. Các câu hỏi trắc nghiệm thường kiểm tra khả năng hiểu và vận dụng các khái niệm cơ bản về hàm số. Các bài tập tự luận yêu cầu học sinh phải trình bày lời giải chi tiết, rõ ràng và chính xác.
Để giúp các bạn học sinh giải quyết bài tập 1.10 một cách hiệu quả, giaitoan.edu.vn xin trình bày lời giải chi tiết cho từng câu hỏi:
Cho hàm số f(x) = √(x-2). Xác định tập xác định của hàm số.
Lời giải:
Hàm số f(x) = √(x-2) xác định khi và chỉ khi biểu thức dưới dấu căn không âm, tức là:
x - 2 ≥ 0
⇔ x ≥ 2
Vậy tập xác định của hàm số là D = [2; +∞).
Cho hàm số f(x) = x2 + 1 và g(x) = 2x - 3. Tính (f + g)(x) và (f - g)(x).
Lời giải:
(f + g)(x) = f(x) + g(x) = (x2 + 1) + (2x - 3) = x2 + 2x - 2
(f - g)(x) = f(x) - g(x) = (x2 + 1) - (2x - 3) = x2 - 2x + 4
Vẽ đồ thị của hàm số y = |x|.
Lời giải:
Hàm số y = |x| được định nghĩa như sau:
Đồ thị của hàm số y = |x| là hai đoạn thẳng:
Ngoài bài tập 1.10, chương 1 còn xuất hiện nhiều dạng bài tập khác. Dưới đây là một số dạng bài tập thường gặp:
Để giải bài tập về hàm số một cách hiệu quả, bạn nên:
Bài tập 1.10 trang 19 SGK Toán 12 tập 1 - Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số. Hy vọng với lời giải chi tiết và các mẹo giải bài tập mà giaitoan.edu.vn đã cung cấp, các bạn học sinh sẽ giải quyết bài tập này một cách dễ dàng và hiệu quả.
Chúc các bạn học tập tốt!