Chào mừng các em học sinh đến với bài giải chi tiết mục 6 trang 38,39 SGK Toán 12 tập 2 - Kết nối tri thức trên giaitoan.edu.vn. Bài viết này cung cấp lời giải đầy đủ, dễ hiểu cho từng bài tập, giúp các em nắm vững kiến thức và tự tin làm bài tập về nhà.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập hiệu quả nhất, hỗ trợ các em học tập tốt môn Toán.
KHOẢNG CÁCH TỪ MỘT ĐIỂM ĐẾN MỘT MẶT PHẲNG
Trả lời câu hỏi Luyện tập 11 trang 39 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, cho hai mặt phẳng \(\left( P \right):x + 3y + z + 2 = 0\) và \(\left( Q \right):x + 3y + z + 5 = 0\)
a) Chứng minh rằng (P) và (Q) song song với nhau.
b) Lấy một điểm thuộc (P), tính khoảng cách từ điểm đó đến (Q). Từ đó tính khoảng cách giữa hai mặt phẳng (P) và (Q).
Phương pháp giải:
Sử dụng kiến thức về điều kiện để hai mặt phẳng song song để chứng minh: Trong không gian Oxyz, cho hai mặt phẳng \(\left( \alpha \right):Ax + By + Cz + D = 0\), \(\left( \beta \right):A'x + B'y + C'z + D' = 0\) với các vectơ pháp tuyến \(\overrightarrow n = \left( {A;B;C} \right),\overrightarrow {n'} = \left( {A';B';C'} \right)\) tương ứng. Khi đó, \(\left( \alpha \right)//\left( \beta \right) \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow {n'} = k\overrightarrow n \\D' \ne kD\end{array} \right.\) với k nào đó.
Sử dụng kiến thức về khoảng cách từ một điểm đến một mặt phẳng để tính: Trong không gian Oxyz, khoảng cách từ điểm \(M\left( {{x_0};{y_0};{z_0}} \right)\) đến mặt phẳng \(\left( P \right):Ax + By + Cz + D = 0\) là \(d\left( {M,\left( P \right)} \right) = \frac{{\left| {A{x_0} + B{y_0} + C{z_0} + D} \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}\).
Lời giải chi tiết:
a) Mặt phẳng (P) có một vectơ pháp tuyến là: \(\overrightarrow {{n_P}} = \left( {1;3;1} \right)\), mặt phẳng (Q) có một vectơ pháp tuyến là: \(\overrightarrow {{n_Q}} = \left( {1;3;1} \right)\). Vì \(\overrightarrow {{n_P}} = \overrightarrow {{n_Q}} \) và \(2 \ne 5\) nên (P) và (Q) song song với nhau.
b) Lấy điểm A(0; 0; -2) thuộc mặt phẳng (P). Ta có: \(d\left( {A,\left( Q \right)} \right) = \frac{{\left| {0 + 3.0 - 2 + 5} \right|}}{{\sqrt {{1^2} + {3^2} + {1^2}} }} = \frac{{3\sqrt {11} }}{{11}}\)
Vì (P) và (Q) song song với nhau nên \(d\left( {\left( P \right),\left( Q \right)} \right) = d\left( {A,\left( Q \right)} \right) = \frac{{3\sqrt {11} }}{{11}}\).
Trả lời câu hỏi Hoạt động 10 trang 38 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, cho điểm \(M\left( {{x_0};{y_0};{z_0}} \right)\) và mặt phẳng \(\left( P \right):Ax + By + Cz + D = 0\) có vectơ pháp tuyến \(\overrightarrow n = \left( {A;B;C} \right)\). Gọi N là hình chiếu vuông góc của M trên (P). (H.5.13)
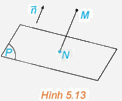
a) Giải thích vì sao tồn tại số k để \(\overrightarrow {MN} = k\overrightarrow n \). Tính tọa độ của N theo k, tọa độ của M và các hệ số A, B, C, D.
b) Thay tọa độ của N vào phương trình mặt phẳng (P) để từ đó tính k theo tọa độ của M và các hệ số A, B, C, D.
c) Từ \(\left| {\overrightarrow {MN} } \right| = \left| k \right|\left| {\overrightarrow n } \right|\), hãy tính độ dài của đoạn thẳng MN theo tọa độ của M và các hệ số A, B, C, D. Từ đó suy ra công thức tính khoảng cách từ điểm M đến mặt phẳng (P).
Phương pháp giải:
Sử dụng kiến thức về vectơ pháp tuyến của mặt phẳng để chứng minh: Vectơ \(\overrightarrow n \ne \overrightarrow 0 \) được gọi là vectơ pháp tuyến của mặt phẳng \(\left( \alpha \right)\) nếu giá của \(\overrightarrow n \) vuông góc với \(\left( \alpha \right)\).
Lời giải chi tiết:
a) Vì N là hình chiếu vuông góc của M trên (P) nên \(MN \bot \left( P \right)\). Mà \(\overrightarrow n \) là vectơ pháp tuyến của mặt phẳng (P) nên hai vectơ \(\overrightarrow {MN} \) và \(\overrightarrow n \) cùng phương. Do đó, tồn tại số k để \(\overrightarrow {MN} = k\overrightarrow n \). Suy ra: \(\left\{ \begin{array}{l}{x_N} - {x_M} = kA\\{y_N} - {y_M} = kB\\{z_N} - {z_M} = kC\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_N} = kA + {x_0}\\{y_N} = kB + {y_0}\\{z_N} = kC + {z_0}\end{array} \right.\) nên \(N\left( {kA + {x_0};kB + {y_0};kC + {z_0}} \right)\)
b) Thay \(x = kA + {x_0};y = kB + {y_0};z = kC + {z_0}\) vào phương trình \(Ax + By + Cz + D = 0\) ta có: \(A\left( {kA + {x_0}} \right) + B\left( {kB + {y_0}} \right) + C\left( {kC + {z_0}} \right) + D = 0\)
\( \Leftrightarrow k{A^2} + A{x_0} + k{B^2} + B{y_0} + k{C^2} + C{z_0} + D = 0\)
\( \Leftrightarrow k\left( {{A^2} + {B^2} + {C^2}} \right) + A{x_0} + B{y_0} + C{z_0} + D = 0\)\( \Leftrightarrow k = \frac{{ - \left( {A{x_0} + B{y_0} + C{z_0} + D} \right)}}{{{A^2} + {B^2} + {C^2}}}\)
c) Ta có: \(\left| {\overrightarrow n } \right| = \sqrt {{A^2} + {B^2} + {C^2}} \) nên \(\left| {\overrightarrow {MN} } \right| = \left| k \right|\left| {\overrightarrow n } \right| = \left| k \right|\sqrt {{A^2} + {B^2} + {C^2}} \) \( = \sqrt {\frac{{{{\left( {A{x_0} + B{y_0} + C{z_0} + D} \right)}^2}\left( {{A^2} + {B^2} + {C^2}} \right)}}{{{{\left( {{A^2} + {B^2} + {C^2}} \right)}^2}}}} \)\( = \frac{{\left| {A{x_0} + B{y_0} + C{z_0} + D} \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}\)
Do đó, công thức tính khoảng cách từ điểm M đến mặt phẳng (P) là:
\(d\left( {M,\left( P \right)} \right) = \frac{{\left| {A{x_0} + B{y_0} + C{z_0} + D} \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}\)
Trả lời câu hỏi Vận dụng 5 trang 39 SGK Toán 12 Kết nối tri thức
Góc quan sát ngang của một camera là \({115^0}\). Trong không gian Oxyz, camera được đặt tại điểm C(1; 2; 4) và chiếu thẳng về phía mặt phẳng \(\left( P \right):x + 2y + 2z + 3 = 0\). Hỏi vùng quan sát được trên mặt phẳng (P) của camera là hình tròn có bán kính bằng bao nhiêu? (Làm tròn kết quả đến chữ số thập phân thứ nhất).
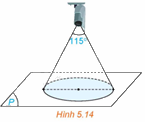
Phương pháp giải:
Sử dụng kiến thức về khoảng cách từ một điểm đến một mặt phẳng để tính: Trong không gian Oxyz, khoảng cách từ điểm \(M\left( {{x_0};{y_0};{z_0}} \right)\) đến mặt phẳng \(\left( P \right):Ax + By + Cz + D = 0\) là \(d\left( {M,\left( P \right)} \right) = \frac{{\left| {A{x_0} + B{y_0} + C{z_0} + D} \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}\).
Lời giải chi tiết:
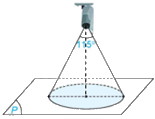
Khoảng cách từ điểm C đến mặt phẳng (P) là: \(d\left( {C,\left( P \right)} \right) = \frac{{\left| {1.1 + 2.2 + 2.4 + 3} \right|}}{{\sqrt {{1^2} + {2^2} + {2^2}} }} = \frac{{16}}{3}\)
Vùng quan sát trên mặt phẳng (P) của camera là hình tròn có bán kính là:
\(R = d\left( {C,\left( P \right)} \right).\tan \frac{{{{115}^0}}}{2} \approx 8,4\)
Trả lời câu hỏi Hoạt động 10 trang 38 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, cho điểm \(M\left( {{x_0};{y_0};{z_0}} \right)\) và mặt phẳng \(\left( P \right):Ax + By + Cz + D = 0\) có vectơ pháp tuyến \(\overrightarrow n = \left( {A;B;C} \right)\). Gọi N là hình chiếu vuông góc của M trên (P). (H.5.13)
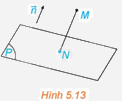
a) Giải thích vì sao tồn tại số k để \(\overrightarrow {MN} = k\overrightarrow n \). Tính tọa độ của N theo k, tọa độ của M và các hệ số A, B, C, D.
b) Thay tọa độ của N vào phương trình mặt phẳng (P) để từ đó tính k theo tọa độ của M và các hệ số A, B, C, D.
c) Từ \(\left| {\overrightarrow {MN} } \right| = \left| k \right|\left| {\overrightarrow n } \right|\), hãy tính độ dài của đoạn thẳng MN theo tọa độ của M và các hệ số A, B, C, D. Từ đó suy ra công thức tính khoảng cách từ điểm M đến mặt phẳng (P).
Phương pháp giải:
Sử dụng kiến thức về vectơ pháp tuyến của mặt phẳng để chứng minh: Vectơ \(\overrightarrow n \ne \overrightarrow 0 \) được gọi là vectơ pháp tuyến của mặt phẳng \(\left( \alpha \right)\) nếu giá của \(\overrightarrow n \) vuông góc với \(\left( \alpha \right)\).
Lời giải chi tiết:
a) Vì N là hình chiếu vuông góc của M trên (P) nên \(MN \bot \left( P \right)\). Mà \(\overrightarrow n \) là vectơ pháp tuyến của mặt phẳng (P) nên hai vectơ \(\overrightarrow {MN} \) và \(\overrightarrow n \) cùng phương. Do đó, tồn tại số k để \(\overrightarrow {MN} = k\overrightarrow n \). Suy ra: \(\left\{ \begin{array}{l}{x_N} - {x_M} = kA\\{y_N} - {y_M} = kB\\{z_N} - {z_M} = kC\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_N} = kA + {x_0}\\{y_N} = kB + {y_0}\\{z_N} = kC + {z_0}\end{array} \right.\) nên \(N\left( {kA + {x_0};kB + {y_0};kC + {z_0}} \right)\)
b) Thay \(x = kA + {x_0};y = kB + {y_0};z = kC + {z_0}\) vào phương trình \(Ax + By + Cz + D = 0\) ta có: \(A\left( {kA + {x_0}} \right) + B\left( {kB + {y_0}} \right) + C\left( {kC + {z_0}} \right) + D = 0\)
\( \Leftrightarrow k{A^2} + A{x_0} + k{B^2} + B{y_0} + k{C^2} + C{z_0} + D = 0\)
\( \Leftrightarrow k\left( {{A^2} + {B^2} + {C^2}} \right) + A{x_0} + B{y_0} + C{z_0} + D = 0\)\( \Leftrightarrow k = \frac{{ - \left( {A{x_0} + B{y_0} + C{z_0} + D} \right)}}{{{A^2} + {B^2} + {C^2}}}\)
c) Ta có: \(\left| {\overrightarrow n } \right| = \sqrt {{A^2} + {B^2} + {C^2}} \) nên \(\left| {\overrightarrow {MN} } \right| = \left| k \right|\left| {\overrightarrow n } \right| = \left| k \right|\sqrt {{A^2} + {B^2} + {C^2}} \) \( = \sqrt {\frac{{{{\left( {A{x_0} + B{y_0} + C{z_0} + D} \right)}^2}\left( {{A^2} + {B^2} + {C^2}} \right)}}{{{{\left( {{A^2} + {B^2} + {C^2}} \right)}^2}}}} \)\( = \frac{{\left| {A{x_0} + B{y_0} + C{z_0} + D} \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}\)
Do đó, công thức tính khoảng cách từ điểm M đến mặt phẳng (P) là:
\(d\left( {M,\left( P \right)} \right) = \frac{{\left| {A{x_0} + B{y_0} + C{z_0} + D} \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}\)
Trả lời câu hỏi Luyện tập 11 trang 39 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, cho hai mặt phẳng \(\left( P \right):x + 3y + z + 2 = 0\) và \(\left( Q \right):x + 3y + z + 5 = 0\)
a) Chứng minh rằng (P) và (Q) song song với nhau.
b) Lấy một điểm thuộc (P), tính khoảng cách từ điểm đó đến (Q). Từ đó tính khoảng cách giữa hai mặt phẳng (P) và (Q).
Phương pháp giải:
Sử dụng kiến thức về điều kiện để hai mặt phẳng song song để chứng minh: Trong không gian Oxyz, cho hai mặt phẳng \(\left( \alpha \right):Ax + By + Cz + D = 0\), \(\left( \beta \right):A'x + B'y + C'z + D' = 0\) với các vectơ pháp tuyến \(\overrightarrow n = \left( {A;B;C} \right),\overrightarrow {n'} = \left( {A';B';C'} \right)\) tương ứng. Khi đó, \(\left( \alpha \right)//\left( \beta \right) \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow {n'} = k\overrightarrow n \\D' \ne kD\end{array} \right.\) với k nào đó.
Sử dụng kiến thức về khoảng cách từ một điểm đến một mặt phẳng để tính: Trong không gian Oxyz, khoảng cách từ điểm \(M\left( {{x_0};{y_0};{z_0}} \right)\) đến mặt phẳng \(\left( P \right):Ax + By + Cz + D = 0\) là \(d\left( {M,\left( P \right)} \right) = \frac{{\left| {A{x_0} + B{y_0} + C{z_0} + D} \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}\).
Lời giải chi tiết:
a) Mặt phẳng (P) có một vectơ pháp tuyến là: \(\overrightarrow {{n_P}} = \left( {1;3;1} \right)\), mặt phẳng (Q) có một vectơ pháp tuyến là: \(\overrightarrow {{n_Q}} = \left( {1;3;1} \right)\). Vì \(\overrightarrow {{n_P}} = \overrightarrow {{n_Q}} \) và \(2 \ne 5\) nên (P) và (Q) song song với nhau.
b) Lấy điểm A(0; 0; -2) thuộc mặt phẳng (P). Ta có: \(d\left( {A,\left( Q \right)} \right) = \frac{{\left| {0 + 3.0 - 2 + 5} \right|}}{{\sqrt {{1^2} + {3^2} + {1^2}} }} = \frac{{3\sqrt {11} }}{{11}}\)
Vì (P) và (Q) song song với nhau nên \(d\left( {\left( P \right),\left( Q \right)} \right) = d\left( {A,\left( Q \right)} \right) = \frac{{3\sqrt {11} }}{{11}}\).
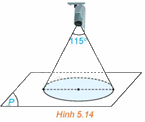
Trả lời câu hỏi Vận dụng 5 trang 39 SGK Toán 12 Kết nối tri thức
Góc quan sát ngang của một camera là \({115^0}\). Trong không gian Oxyz, camera được đặt tại điểm C(1; 2; 4) và chiếu thẳng về phía mặt phẳng \(\left( P \right):x + 2y + 2z + 3 = 0\). Hỏi vùng quan sát được trên mặt phẳng (P) của camera là hình tròn có bán kính bằng bao nhiêu? (Làm tròn kết quả đến chữ số thập phân thứ nhất).
Phương pháp giải:
Sử dụng kiến thức về khoảng cách từ một điểm đến một mặt phẳng để tính: Trong không gian Oxyz, khoảng cách từ điểm \(M\left( {{x_0};{y_0};{z_0}} \right)\) đến mặt phẳng \(\left( P \right):Ax + By + Cz + D = 0\) là \(d\left( {M,\left( P \right)} \right) = \frac{{\left| {A{x_0} + B{y_0} + C{z_0} + D} \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}\).
Lời giải chi tiết:
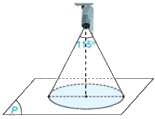
Khoảng cách từ điểm C đến mặt phẳng (P) là: \(d\left( {C,\left( P \right)} \right) = \frac{{\left| {1.1 + 2.2 + 2.4 + 3} \right|}}{{\sqrt {{1^2} + {2^2} + {2^2}} }} = \frac{{16}}{3}\)
Vùng quan sát trên mặt phẳng (P) của camera là hình tròn có bán kính là:
\(R = d\left( {C,\left( P \right)} \right).\tan \frac{{{{115}^0}}}{2} \approx 8,4\)
Mục 6 trong SGK Toán 12 tập 2 - Kết nối tri thức tập trung vào các kiến thức về Số phức. Đây là một phần quan trọng trong chương trình Toán học lớp 12, đòi hỏi học sinh phải nắm vững các khái niệm cơ bản và kỹ năng giải bài tập liên quan. Bài viết này sẽ cung cấp lời giải chi tiết cho từng bài tập trong mục 6, trang 38 và 39, giúp các em hiểu rõ hơn về các khái niệm và phương pháp giải quyết các bài toán về số phức.
Đề bài: Tìm phần thực và phần ảo của các số phức sau: a) 3 + 2i; b) -1 - 5i; c) 0,5 - 0,8i; d) -7.
Lời giải:
Đề bài: Thực hiện các phép tính sau: a) (2 + 3i) + (1 - i); b) (5 - 2i) - (3 + 4i); c) (1 + i)(2 - 3i); d) (4 + 5i)/(1 - i).
Lời giải:
Đề bài: Tìm số phức liên hợp của các số phức sau: a) 2 - 3i; b) -1 + i; c) 5; d) -4i.
Lời giải:
Số phức không chỉ là một khái niệm trừu tượng trong Toán học mà còn có nhiều ứng dụng thực tế trong các lĩnh vực như:
Hy vọng bài giải chi tiết này sẽ giúp các em hiểu rõ hơn về mục 6 trang 38,39 SGK Toán 12 tập 2 - Kết nối tri thức. Chúc các em học tập tốt!