Chào mừng các em học sinh đến với bài giải chi tiết mục 5 trang 37,38 SGK Toán 12 tập 2 - Kết nối tri thức trên giaitoan.edu.vn. Bài viết này cung cấp lời giải đầy đủ, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập liên quan.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng cao, hỗ trợ các em học tập hiệu quả và đạt kết quả tốt nhất.
ĐIỀU KIỆN ĐỂ HAI MẶT PHẲNG SONG SONG VỚI NHAU
Trả lời câu hỏi Luyện tập 10 trang 37 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, cho hai mặt phẳng: \(\left( \alpha \right):5x + 2y - 4z + 6 = 0\) và \(\left( \beta \right):10x + 4y - 2z + 12 = 0\)
a) Hỏi \(\left( \alpha \right)\) và \(\left( \beta \right)\) có song song với nhau hay không?
b) Chứng minh rằng điểm \(M\left( {1; - 3;5} \right)\) không thuộc mặt phẳng \(\left( \alpha \right)\) nhưng thuộc mặt phẳng \(\left( \beta \right)\).
c) Viết phương trình mặt phẳng (P) đi qua \(M\left( {1; - 3;5} \right)\) và song song với \(\left( \alpha \right)\).
Phương pháp giải:
Sử dụng kiến thức về điều kiện để hai mặt phẳng song song hoặc trùng nhau để tính: Trong không gian Oxyz, cho hai mặt phẳng \(\left( \alpha \right):Ax + By + Cz + D = 0\), \(\left( \beta \right):A'x + B'y + C'z + D' = 0\) với các vectơ pháp tuyến \(\overrightarrow n = \left( {A;B;C} \right),\overrightarrow {n'} = \left( {A';B';C'} \right)\) tương ứng. Khi đó, \(\left( \alpha \right)//\left( \beta \right) \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow {n'} = k\overrightarrow n \\D' \ne kD\end{array} \right.\) với k nào đó.
Sử dụng kiến thức về điều kiện để hai mặt phẳng song song để tính: Nếu hai mặt phẳng song song với nhau thì vectơ pháp tuyến của mặt phẳng này cũng là vectơ pháp tuyến của mặt phẳng kia.
Lời giải chi tiết:
a) Mặt phẳng \(\left( \alpha \right)\) có một vectơ pháp tuyến là: \(\overrightarrow {{n_\alpha }} = \left( {5;2; - 4} \right)\), mặt phẳng \(\left( \beta \right)\) có một vectơ pháp tuyến là: \(\overrightarrow {{n_\beta }} = \left( {10;4; - 2} \right)\).
Vì \(\frac{5}{{10}} = \frac{4}{2} \ne \frac{{ - 4}}{2}\) nên \(\overrightarrow {{n_\alpha }} \) và \(\overrightarrow {{n_\beta }} \) không cùng phương. Do đó, hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\) không song song với nhau.
b) Vì \(5.1 - 3.2 - 4.5 + 6 = 5 - 6 - 20 + 6 = - 15 \ne 0\) nên điểm \(M\left( {1; - 3;5} \right)\) không thuộc mặt phẳng \(\left( \alpha \right)\).
Vì \(10.1 + 4.\left( { - 3} \right) - 2.5 + 12 = 0\) nên điểm \(M\left( {1; - 3;5} \right)\) thuộc mặt phẳng \(\left( \beta \right)\).
c) Vì mặt phẳng (P) song song với \(\left( \alpha \right)\) nên mặt phẳng (P) nhận \(\overrightarrow {{n_\alpha }} = \left( {5;2; - 4} \right)\) làm một vectơ pháp tuyến. Mà điểm \(M\left( {1; - 3;5} \right)\) thuộc (P) nên phương trình mặt phẳng (P) là:
\(5\left( {x - 1} \right) + 2\left( {y + 3} \right) - 4\left( {z - 5} \right) = 0 \Leftrightarrow 5x + 2y - 4z + 21 = 0\)
Trả lời câu hỏi Hoạt động 9 trang 37 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, cho hai mặt phẳng \(\left( \alpha \right):Ax + By + Cz + D = 0\), \(\left( \beta \right):A'x + B'y + C'z + D' = 0\) với các vectơ pháp tuyến \(\overrightarrow n = \left( {A;B;C} \right),\overrightarrow {n'} = \left( {A';B';C'} \right)\) tương ứng.
Nếu hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\) song song hoặc trùng nhau thì các vectơ \(\overrightarrow n ,\overrightarrow {n'} \) có mối quan hệ gì?
Phương pháp giải:
Sử dụng kiến thức về vectơ pháp tuyến của mặt phẳng: Vectơ \(\overrightarrow n \ne \overrightarrow 0 \) được gọi là vectơ pháp tuyến của mặt phẳng \(\left( \alpha \right)\) nếu \(\overrightarrow n \) vuông góc với \(\left( \alpha \right)\).
Lời giải chi tiết:
Nếu hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\) song song hoặc trùng nhau thì giá của các vectơ \(\overrightarrow n ,\overrightarrow {n'} \) song song song hoặc trùng nhau. Do đó, các vectơ \(\overrightarrow n ,\overrightarrow {n'} \) cùng phương với nhau.
Trả lời câu hỏi Hoạt động 9 trang 37 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, cho hai mặt phẳng \(\left( \alpha \right):Ax + By + Cz + D = 0\), \(\left( \beta \right):A'x + B'y + C'z + D' = 0\) với các vectơ pháp tuyến \(\overrightarrow n = \left( {A;B;C} \right),\overrightarrow {n'} = \left( {A';B';C'} \right)\) tương ứng.
Nếu hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\) song song hoặc trùng nhau thì các vectơ \(\overrightarrow n ,\overrightarrow {n'} \) có mối quan hệ gì?
Phương pháp giải:
Sử dụng kiến thức về vectơ pháp tuyến của mặt phẳng: Vectơ \(\overrightarrow n \ne \overrightarrow 0 \) được gọi là vectơ pháp tuyến của mặt phẳng \(\left( \alpha \right)\) nếu \(\overrightarrow n \) vuông góc với \(\left( \alpha \right)\).
Lời giải chi tiết:
Nếu hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\) song song hoặc trùng nhau thì giá của các vectơ \(\overrightarrow n ,\overrightarrow {n'} \) song song song hoặc trùng nhau. Do đó, các vectơ \(\overrightarrow n ,\overrightarrow {n'} \) cùng phương với nhau.
Trả lời câu hỏi Luyện tập 10 trang 37 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, cho hai mặt phẳng: \(\left( \alpha \right):5x + 2y - 4z + 6 = 0\) và \(\left( \beta \right):10x + 4y - 2z + 12 = 0\)
a) Hỏi \(\left( \alpha \right)\) và \(\left( \beta \right)\) có song song với nhau hay không?
b) Chứng minh rằng điểm \(M\left( {1; - 3;5} \right)\) không thuộc mặt phẳng \(\left( \alpha \right)\) nhưng thuộc mặt phẳng \(\left( \beta \right)\).
c) Viết phương trình mặt phẳng (P) đi qua \(M\left( {1; - 3;5} \right)\) và song song với \(\left( \alpha \right)\).
Phương pháp giải:
Sử dụng kiến thức về điều kiện để hai mặt phẳng song song hoặc trùng nhau để tính: Trong không gian Oxyz, cho hai mặt phẳng \(\left( \alpha \right):Ax + By + Cz + D = 0\), \(\left( \beta \right):A'x + B'y + C'z + D' = 0\) với các vectơ pháp tuyến \(\overrightarrow n = \left( {A;B;C} \right),\overrightarrow {n'} = \left( {A';B';C'} \right)\) tương ứng. Khi đó, \(\left( \alpha \right)//\left( \beta \right) \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow {n'} = k\overrightarrow n \\D' \ne kD\end{array} \right.\) với k nào đó.
Sử dụng kiến thức về điều kiện để hai mặt phẳng song song để tính: Nếu hai mặt phẳng song song với nhau thì vectơ pháp tuyến của mặt phẳng này cũng là vectơ pháp tuyến của mặt phẳng kia.
Lời giải chi tiết:
a) Mặt phẳng \(\left( \alpha \right)\) có một vectơ pháp tuyến là: \(\overrightarrow {{n_\alpha }} = \left( {5;2; - 4} \right)\), mặt phẳng \(\left( \beta \right)\) có một vectơ pháp tuyến là: \(\overrightarrow {{n_\beta }} = \left( {10;4; - 2} \right)\).
Vì \(\frac{5}{{10}} = \frac{4}{2} \ne \frac{{ - 4}}{2}\) nên \(\overrightarrow {{n_\alpha }} \) và \(\overrightarrow {{n_\beta }} \) không cùng phương. Do đó, hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\) không song song với nhau.
b) Vì \(5.1 - 3.2 - 4.5 + 6 = 5 - 6 - 20 + 6 = - 15 \ne 0\) nên điểm \(M\left( {1; - 3;5} \right)\) không thuộc mặt phẳng \(\left( \alpha \right)\).
Vì \(10.1 + 4.\left( { - 3} \right) - 2.5 + 12 = 0\) nên điểm \(M\left( {1; - 3;5} \right)\) thuộc mặt phẳng \(\left( \beta \right)\).
c) Vì mặt phẳng (P) song song với \(\left( \alpha \right)\) nên mặt phẳng (P) nhận \(\overrightarrow {{n_\alpha }} = \left( {5;2; - 4} \right)\) làm một vectơ pháp tuyến. Mà điểm \(M\left( {1; - 3;5} \right)\) thuộc (P) nên phương trình mặt phẳng (P) là:
\(5\left( {x - 1} \right) + 2\left( {y + 3} \right) - 4\left( {z - 5} \right) = 0 \Leftrightarrow 5x + 2y - 4z + 21 = 0\)
Trả lời câu hỏi Vận dụng 4 trang 37 SGK Toán 12 Kết nối tri thức
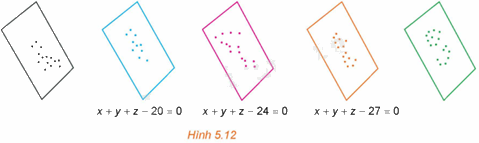
Trong một kì thi tuyển sinh có ba môn thi Toán, Văn, Tiếng Anh. Trong không gian Oxyz, người ta biểu diễn kết quả thi của mỗi thí sinh bởi điểm có hoành độ, tung độ, cao độ tương ứng là điểm Toán, Văn, Tiếng Anh của thí sinh đó.
a) Chứng minh rằng các điểm biểu diễn tương ứng với các thí sinh có tổng số điểm ba môn bằng 27 (nếu có) cùng thuộc mặt phẳng có phương trình \(x + y + z - 27 = 0\).
b) Chứng minh rằng tồn tại một số mặt phẳng đôi một song song với nhau sao cho hai điểm biểu diễn ứng với hai thí sinh có tổng số điểm thi bằng nhau thì cùng thuộc một mặt phẳng trong số các mặt phẳng đó.
Phương pháp giải:
Sử dụng kiến thức về điều kiện để hai mặt phẳng song song để chứng minh: Nếu hai mặt phẳng song song với nhau thì vectơ pháp tuyến của mặt phẳng này cũng là vectơ pháp tuyến của mặt phẳng kia.
Lời giải chi tiết:
a) Gọi điểm Toán, Văn, Tiếng Anh của một thí sinh lần lượt là \({x_0};{y_0};{z_0}\) sao cho tổng điểm của thí sinh đó là 27. Khi đó, \({x_0} + {y_0} + {z_0} = 27\). Suy ra, điểm \(M\left( {{x_0};{y_0};{z_0}} \right)\) biểu diễn kết quả thi của thí sinh đó.
Thay \(x = {x_0};y = {y_0},z = {z_0}\) vào phương trình \(x + y + z - 27 = 0\) ta có:
${{x}_{0}}+{{y}_{0}}+{{z}_{0}}-27=0\Leftrightarrow 27-27=0\left( LD \right)$
Do đó, điểm \(M\left( {{x_0};{y_0};{z_0}} \right)\) thuộc mặt phẳng có phương trình \(x + y + z - 27 = 0\).
Vậy các điểm biểu diễn tương ứng với các thí sinh có tổng số điểm ba môn bằng 27 (nếu có) cùng thuộc mặt phẳng có phương trình \(x + y + z - 27 = 0\).
b) Xét phương trình mặt phẳng (M): \(x + y + z - 24 = 0\)
Gọi điểm Toán, Văn, Tiếng Anh của một thí sinh lần lượt là \({x_1};{y_1};{z_1}\) sao cho tổng điểm của thí sinh đó là 24. Khi đó, \({x_1} + {y_1} + {z_1} = 24\). Khi đó, điểm \(A\left( {{x_1};{y_1};{z_1}} \right)\) biểu diễn kết quả thi của thí sinh đó.
Thay \(x = {x_1};y = {y_1},z = {z_1}\) vào phương trình \(x + y + z - 24 = 0\) ta có:
${{x}_{1}}+{{y}_{1}}+{{z}_{1}}-24=0\Leftrightarrow 24-24=0\left( L \right)$
Do đó, điểm \(A\left( {{x_1};{y_1};{z_1}} \right)\) thuộc mặt phẳng có phương trình \(x + y + z - 24 = 0\).
Vậy các điểm biểu diễn tương ứng với các thí sinh có tổng số điểm ba môn bằng 24 (nếu có) cùng thuộc mặt phẳng (M).
Xét phương trình mặt phẳng (N): \(x + y + z - 20 = 0\)
Gọi điểm Toán, Văn, Tiếng Anh của một thí sinh lần lượt là \({x_2};{y_2};{z_2}\) sao cho tổng điểm của thí sinh đó là 20. Khi đó, \({x_2} + {y_2} + {z_2} = 20\). Khi đó, điểm \(B\left( {{x_2};{y_2};{z_2}} \right)\) biểu diễn kết quả thi của thí sinh đó.
Thay \(x = {x_2};y = {y_2},z = {z_2}\) vào phương trình \(x + y + z - 20 = 0\) ta có:
${{x}_{2}}+{{y}_{2}}+{{z}_{2}}-20=0\Leftrightarrow 20-20=0\left( LD \right)$
Do đó, điểm \(B\left( {{x_2};{y_2};{z_2}} \right)\) thuộc mặt phẳng (N).
Vậy các điểm biểu diễn tương ứng với các thí sinh có tổng số điểm ba môn bằng 20 cùng thuộc mặt phẳng có phương trình (N).
Theo a, các điểm biểu diễn tương ứng với các thí sinh có tổng số điểm ba môn bằng 27 cùng thuộc mặt phẳng (P) có phương trình \(x + y + z - 27 = 0\).
Ta thấy ba mặt phẳng (M), (N), (P) có vectơ pháp tuyến \(\overrightarrow n \left( {1;1;1} \right)\) và \( - 24 \ne - 20 \ne - 27\) nên ba mặt phẳng (M), (N), (P) song song với nhau.
Từ đó ta có kết luận: Tồn tại một số mặt phẳng đôi một song song với nhau sao cho hai điểm biểu diễn ứng với hai thí sinh có tổng số điểm thi bằng nhau thì cùng thuộc một mặt phẳng trong số các mặt phẳng đó.
Trả lời câu hỏi Vận dụng 4 trang 37 SGK Toán 12 Kết nối tri thức
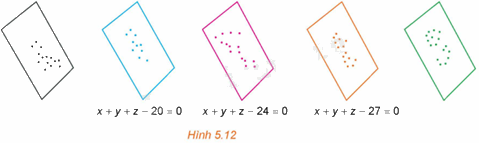
Trong một kì thi tuyển sinh có ba môn thi Toán, Văn, Tiếng Anh. Trong không gian Oxyz, người ta biểu diễn kết quả thi của mỗi thí sinh bởi điểm có hoành độ, tung độ, cao độ tương ứng là điểm Toán, Văn, Tiếng Anh của thí sinh đó.
a) Chứng minh rằng các điểm biểu diễn tương ứng với các thí sinh có tổng số điểm ba môn bằng 27 (nếu có) cùng thuộc mặt phẳng có phương trình \(x + y + z - 27 = 0\).
b) Chứng minh rằng tồn tại một số mặt phẳng đôi một song song với nhau sao cho hai điểm biểu diễn ứng với hai thí sinh có tổng số điểm thi bằng nhau thì cùng thuộc một mặt phẳng trong số các mặt phẳng đó.
Phương pháp giải:
Sử dụng kiến thức về điều kiện để hai mặt phẳng song song để chứng minh: Nếu hai mặt phẳng song song với nhau thì vectơ pháp tuyến của mặt phẳng này cũng là vectơ pháp tuyến của mặt phẳng kia.
Lời giải chi tiết:
a) Gọi điểm Toán, Văn, Tiếng Anh của một thí sinh lần lượt là \({x_0};{y_0};{z_0}\) sao cho tổng điểm của thí sinh đó là 27. Khi đó, \({x_0} + {y_0} + {z_0} = 27\). Suy ra, điểm \(M\left( {{x_0};{y_0};{z_0}} \right)\) biểu diễn kết quả thi của thí sinh đó.
Thay \(x = {x_0};y = {y_0},z = {z_0}\) vào phương trình \(x + y + z - 27 = 0\) ta có:
${{x}_{0}}+{{y}_{0}}+{{z}_{0}}-27=0\Leftrightarrow 27-27=0\left( LD \right)$
Do đó, điểm \(M\left( {{x_0};{y_0};{z_0}} \right)\) thuộc mặt phẳng có phương trình \(x + y + z - 27 = 0\).
Vậy các điểm biểu diễn tương ứng với các thí sinh có tổng số điểm ba môn bằng 27 (nếu có) cùng thuộc mặt phẳng có phương trình \(x + y + z - 27 = 0\).
b) Xét phương trình mặt phẳng (M): \(x + y + z - 24 = 0\)
Gọi điểm Toán, Văn, Tiếng Anh của một thí sinh lần lượt là \({x_1};{y_1};{z_1}\) sao cho tổng điểm của thí sinh đó là 24. Khi đó, \({x_1} + {y_1} + {z_1} = 24\). Khi đó, điểm \(A\left( {{x_1};{y_1};{z_1}} \right)\) biểu diễn kết quả thi của thí sinh đó.
Thay \(x = {x_1};y = {y_1},z = {z_1}\) vào phương trình \(x + y + z - 24 = 0\) ta có:
${{x}_{1}}+{{y}_{1}}+{{z}_{1}}-24=0\Leftrightarrow 24-24=0\left( L \right)$
Do đó, điểm \(A\left( {{x_1};{y_1};{z_1}} \right)\) thuộc mặt phẳng có phương trình \(x + y + z - 24 = 0\).
Vậy các điểm biểu diễn tương ứng với các thí sinh có tổng số điểm ba môn bằng 24 (nếu có) cùng thuộc mặt phẳng (M).
Xét phương trình mặt phẳng (N): \(x + y + z - 20 = 0\)
Gọi điểm Toán, Văn, Tiếng Anh của một thí sinh lần lượt là \({x_2};{y_2};{z_2}\) sao cho tổng điểm của thí sinh đó là 20. Khi đó, \({x_2} + {y_2} + {z_2} = 20\). Khi đó, điểm \(B\left( {{x_2};{y_2};{z_2}} \right)\) biểu diễn kết quả thi của thí sinh đó.
Thay \(x = {x_2};y = {y_2},z = {z_2}\) vào phương trình \(x + y + z - 20 = 0\) ta có:
${{x}_{2}}+{{y}_{2}}+{{z}_{2}}-20=0\Leftrightarrow 20-20=0\left( LD \right)$
Do đó, điểm \(B\left( {{x_2};{y_2};{z_2}} \right)\) thuộc mặt phẳng (N).
Vậy các điểm biểu diễn tương ứng với các thí sinh có tổng số điểm ba môn bằng 20 cùng thuộc mặt phẳng có phương trình (N).
Theo a, các điểm biểu diễn tương ứng với các thí sinh có tổng số điểm ba môn bằng 27 cùng thuộc mặt phẳng (P) có phương trình \(x + y + z - 27 = 0\).
Ta thấy ba mặt phẳng (M), (N), (P) có vectơ pháp tuyến \(\overrightarrow n \left( {1;1;1} \right)\) và \( - 24 \ne - 20 \ne - 27\) nên ba mặt phẳng (M), (N), (P) song song với nhau.
Từ đó ta có kết luận: Tồn tại một số mặt phẳng đôi một song song với nhau sao cho hai điểm biểu diễn ứng với hai thí sinh có tổng số điểm thi bằng nhau thì cùng thuộc một mặt phẳng trong số các mặt phẳng đó.
Mục 5 trong SGK Toán 12 tập 2 - Kết nối tri thức tập trung vào việc ôn tập chương về các số phức. Đây là một phần quan trọng, thường xuyên xuất hiện trong các kỳ thi THPT Quốc gia. Việc nắm vững kiến thức về số phức, các phép toán trên số phức, và ứng dụng của chúng là điều cần thiết để đạt điểm cao trong môn Toán.
Mục 5 bao gồm các bài tập tổng hợp, giúp học sinh rèn luyện kỹ năng giải quyết các vấn đề liên quan đến:
Để tìm phần thực và phần ảo của một số phức z = a + bi, ta chỉ cần xác định giá trị của a (phần thực) và b (phần ảo). Ví dụ, nếu z = 3 - 2i, thì phần thực của z là 3 và phần ảo của z là -2.
Để cộng hoặc trừ hai số phức, ta cộng hoặc trừ các phần thực và phần ảo tương ứng. Ví dụ, (2 + 3i) + (1 - i) = (2 + 1) + (3 - 1)i = 3 + 2i.
Để nhân hai số phức, ta sử dụng công thức (a + bi)(c + di) = (ac - bd) + (ad + bc)i. Ví dụ, (1 + i)(2 - i) = (1*2 - 1*(-1)) + (1*(-1) + 1*2)i = 3 + i.
Để chia hai số phức, ta nhân cả tử và mẫu với số phức liên hợp của mẫu. Ví dụ, (1 + i)/(2 - i) = ((1 + i)(2 + i))/((2 - i)(2 + i)) = (2 + i + 2i - 1)/(4 + 1) = (1 + 3i)/5 = 1/5 + 3/5i.
Module của số phức z = a + bi được tính bằng công thức |z| = √(a² + b²). Ví dụ, nếu z = 3 + 4i, thì |z| = √(3² + 4²) = 5.
Số phức không chỉ là một khái niệm trừu tượng trong toán học mà còn có nhiều ứng dụng trong thực tế, như:
Hy vọng bài giải chi tiết mục 5 trang 37,38 SGK Toán 12 tập 2 - Kết nối tri thức trên giaitoan.edu.vn sẽ giúp các em học sinh hiểu rõ hơn về các kiến thức và kỹ năng liên quan đến số phức. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!
| Công thức | Mô tả |
|---|---|
| |z| = √(a² + b²) | Module của số phức z = a + bi |
| z* = a - bi | Số phức liên hợp của z = a + bi |