Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 12. Bài viết này sẽ hướng dẫn bạn cách giải bài tập 1.16 trang 25 SGK Toán 12 tập 1 - Kết nối tri thức một cách nhanh chóng và hiệu quả.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp bạn nắm vững kiến thức và đạt kết quả cao trong môn Toán.
Hình 1.26 là đồ thị của hàm số (y = fleft( x right) = frac{{2{x^2}}}{{{x^2} - 1}}) Sử dụng đồ thị này, hãy: a) Viết kết quả của các giới hạn sau: (mathop {lim }limits_{x to - infty } fleft( x right)); (mathop {lim }limits_{x to + infty } fleft( x right)); (mathop {lim }limits_{x to {1^ - }} fleft( x right)); (mathop {lim }limits_{x to - {1^ + }} fleft( x right)) b) Chỉ ra các tiệm cận của đồ thị hàm số đã cho.
Đề bài
Hình 1.26 là đồ thị của hàm số \(y = f\left( x \right) = \frac{{2{x^2}}}{{{x^2} - 1}}\)
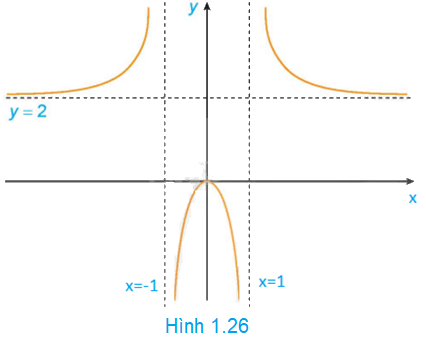
Sử dụng đồ thị này, hãy:a) Viết kết quả của các giới hạn sau: \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right)\); \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right)\); \(\mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right)\); \(\mathop {\lim }\limits_{x \to - {1^ + }} f\left( x \right)\)b) Chỉ ra các tiệm cận của đồ thị hàm số đã cho.
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về khái niệm tiệm cận ngang của đồ thị hàm số để tìm tiệm cận ngang: Đường thẳng \(y = {y_0}\) gọi là đường tiệm cận ngang (gọi tắt là tiệm cận ngang) của đồ thị hàm số \(y = f\left( x \right)\) nếu \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = {y_0}\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = {y_0}\)
Sử dụng kiến thức về khái niệm tiệm cận đứng của đồ thị hàm số để tìm tiệm cận đứng: Đường thẳng \(x = {x_0}\) gọi là đường tiệm cận đứng (gọi tắt là tiệm cận đứng) của đồ thị hàm số \(y = f\left( x \right)\) nếu ít nhất một trong các điều kiện sau được thỏa mãn: \(\mathop {\lim }\limits_{x \to x_0^ + } f\left( x \right) = + \infty \); \(\mathop {\lim }\limits_{x \to x_0^ - } f\left( x \right) = - \infty \); \(\mathop {\lim }\limits_{x \to x_0^ + } f\left( x \right) = - \infty \); \(\mathop {\lim }\limits_{x \to x_0^ - } f\left( x \right) = + \infty \)
Lời giải chi tiết
a) \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = 2\); \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 2\); \(\mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right) = - \infty \); \(\mathop {\lim }\limits_{x \to - {1^ + }} f\left( x \right) = - \infty \)
b) Do đó, tiệm cận đứng của đồ thị hàm số là \(x = 1;x = - 1\).
Tiệm cận ngang của đồ thị hàm số là \(y = 2\)
Bài tập 1.16 trang 25 SGK Toán 12 tập 1 - Kết nối tri thức thuộc chương 1: Hàm số và đồ thị. Bài tập này thường liên quan đến việc xác định tính đơn điệu của hàm số, tìm khoảng đồng biến, nghịch biến và cực trị của hàm số. Để giải bài tập này, học sinh cần nắm vững các kiến thức về đạo hàm, điều kiện cần và đủ để hàm số đạt cực trị, và các phương pháp xét dấu đạo hàm.
Giả sử hàm số cần xét là f(x) = x3 - 3x2 + 2.
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| f'(x) | + | - | + | |
| f(x) | Đồng biến | Nghịch biến | Đồng biến |
Để củng cố kiến thức và kỹ năng giải bài tập về hàm số, bạn có thể luyện tập thêm với các bài tập tương tự trong SGK Toán 12 tập 1 - Kết nối tri thức và các đề thi thử Toán 12. Ngoài ra, bạn có thể tham khảo các tài liệu học tập trực tuyến và các video hướng dẫn giải bài tập trên giaitoan.edu.vn.
Bài tập 1.16 trang 25 SGK Toán 12 tập 1 - Kết nối tri thức là một bài tập quan trọng giúp học sinh hiểu rõ hơn về tính đơn điệu và cực trị của hàm số. Bằng cách nắm vững các kiến thức và phương pháp giải bài tập, bạn có thể tự tin giải quyết các bài toán tương tự và đạt kết quả tốt trong môn Toán.