Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 12. Mục 2 trang 95 SGK Toán 12 tập 1 - Kết nối tri thức là một phần quan trọng trong chương trình học, đòi hỏi học sinh nắm vững kiến thức và kỹ năng giải quyết vấn đề.
Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn lời giải chi tiết, giúp bạn hiểu rõ bản chất của bài toán và áp dụng vào các bài tập tương tự.
Tóm tắt và phân tích dữ liệu
Trả lời câu hỏi Hoạt động 4 trang 95 SGK Toán 12 Kết nối tri thức
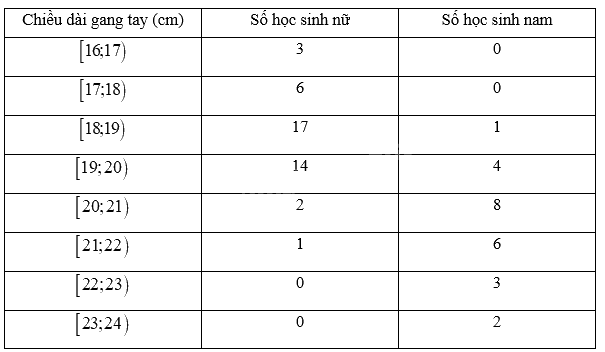
Bảng tần số sau đây là dữ liệu thu được trên một lớp học. Hãy thực hiện HĐ3 cho mẫu số liệu này.
Phương pháp giải:
Sử dụng kiến thức về phương sai của mẫu số liệu ghép nhóm để tính: Phương sai của mẫu số liệu ghép nhóm, kí hiệu là \({s^2}\), là một số được tính theo công thức sau: \({s^2} = \frac{1}{n}\left( {{m_1}x_1^2 + ... + {m_k}x_k^2} \right) - {\left( {\overline x } \right)^2}\), trong đó \(n = {m_1} + ... + {m_k}\) với \(\overline x = \frac{{{m_1}{x_1} + ... + {m_k}{x_k}}}{n}\) là số trung bình của mẫu số liệu ghép nhóm.
Sử dụng kiến thức độ lệch chuẩn của mẫu số liệu ghép nhóm để tính: Độ lệch chuẩn của mẫu số liệu ghép nhóm, kí hiệu là s, là căn bậc hai số học của phương sai của mẫu số liệu ghép nhóm, tức là \(s = \sqrt {{s^2}} \)
Sử dụng kiến thức về hệ số biến thiên để tính hệ số biến thiên độ dài gang tay: Hệ số biến thiên tính theo công thức: \(cv = \frac{s}{{\overline x }}\), trong đó: s là độ lệch chuẩn của mẫu số liệu, \(\overline x \) là giá trị trung bình của mẫu số liệu
Lời giải chi tiết:
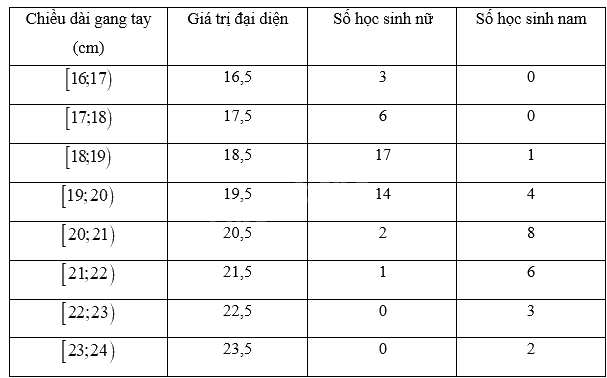
a) Bảng số liệu với giá trị đại diện
Chiều dài gang tay trung bình của học sinh nam trong lớp là:
\(\overline {{x_1}} = \frac{{18,5.1 + 19,5.4 + 20,5.8 + 21,5.6 + 22,5.3 + 23,5.2}}{{1 + 4 + 8 + 6 + 3 + 2}} = 21\left( {cm} \right)\)
Chiều dài gang tay trung bình của học sinh nữ trong lớp là:
\(\overline {{x_2}} = \frac{{16,5.3 + 17,5.6 + 18,5.17 + 19,5.14 + 20,5.2 + 21,5.1}}{{3 + 6 + 17 + 14 + 2 + 1}} = \frac{{1609}}{{86}}\left( {cm} \right)\)
b) Chiều dài gang tay của học sinh nam có:
Phương sai:
\(s_1^2 = \frac{1}{{24}}\left( {1.18,{5^2} + 4.19,{5^2} + 8.20,{5^2} + 6.21,{5^2} + 3.22,{5^2} + 2.23,{5^2}} \right) - {21^2} = \frac{{19}}{{12}}\)
Độ lệch chuẩn: \({s_1} = \sqrt {\frac{{19}}{{12}}} = \frac{{\sqrt {57} }}{6}\)
Hệ số biến thiên: \(c{v_1} = \frac{{{s_1}}}{{\overline {{x_1}} }} = \frac{{\frac{{\sqrt {57} }}{6}}}{{21}} \approx 0,0599\)
Chiều dài gang tay của học sinh nữ có:
Phương sai:
\(s_2^2 = \frac{1}{{43}}\left( {16,{5^2}.3 + 17,{5^2}.6 + 18,{5^2}.17 + 19,{5^2}.14 + 20,{5^2}.2 + 21,{5^2}.1} \right) - {\left( {\frac{{1609}}{{86}}} \right)^2} \approx 1,1\)
Độ lệch chuẩn: \({s_2} = \sqrt {1,1} \approx 1,05\)
Hệ số biến thiên: \(c{v_2} = \frac{{{s_2}}}{{\overline {{x_2}} }} = \frac{{1,05}}{{\frac{{1609}}{{86}}}} \approx 0,0561\)
Vì \(c{v_1} > c{v_2}\) nên độ dài gang tay học sinh nam phân tán nhiều hơn độ dài gang tay học sinh nữ trong lớp.
Trả lời câu hỏi Hoạt động 3 trang 95 SGK Toán 12 Kết nối tri thức
Sử dụng bảng tần số thu được ở HĐ2, em hãy:
a) Tính độ gang tay trung bình của các học sinh nữ, học sinh nam trong lớp và so sánh.
b) Tính phương sai và độ lệch chuẩn và từ đó tính hệ số biến thiên độ dài gang tay của hai nhóm học sinh này và so sánh.
Phương pháp giải:
Sử dụng kiến thức về phương sai của mẫu số liệu ghép nhóm để tính: Phương sai của mẫu số liệu ghép nhóm, kí hiệu là \({s^2}\), là một số được tính theo công thức sau: \({s^2} = \frac{1}{n}\left( {{m_1}x_1^2 + ... + {m_k}x_k^2} \right) - {\left( {\overline x } \right)^2}\), trong đó với là số trung bình của mẫu số liệu ghép nhóm.
Sử dụng kiến thức độ lệch chuẩn của mẫu số liệu ghép nhóm để tính: Độ lệch chuẩn của mẫu số liệu ghép nhóm, kí hiệu là s, là căn bậc \(n = {m_1} + ... + {m_k}\)hai số học của phương sai của mẫu số liệu ghép nhóm, tức là \(s = \sqrt {{s^2}} \)
Sử dụng kiến thức về hệ số biến thiên để tính hệ số biến thiên độ dài gang tay: Hệ số biến thiên tính theo công thức: \(cv = \frac{s}{{\overline x }}\), trong đó: s là độ lệch chuẩn của mẫu số liệu, \(\overline x \) là giá trị trung bình của mẫu số liệu
Lời giải chi tiết:
a) Bảng số liệu với giá trị đại diện
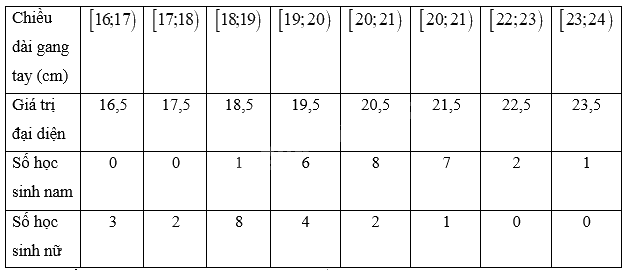
Chiều dài gang tay trung bình của học sinh nam trong lớp là:
\(\overline {{x_1}} = \frac{{18,5.1 + 19,5.6 + 20,5.8 + 21,5.7 + 22,5.2 + 23,5.1}}{{1 + 6 + 8 + 7 + 2 + 1}} = 20,74\left( {cm} \right)\)
Chiều dài gang tay trung bình của học sinh nữ trong lớp là:
\(\overline {{x_2}} = \frac{{16,5.3 + 17,5.2 + 18,5.8 + 19,5.4 + 20,5.2 + 21,5.1}}{{3 + 2 + 8 + 4 + 2 + 1}} = 18,65\left( {cm} \right)\)
b) Chiều dài gang tay của học sinh nam:
Phương sai:
\(s_1^2 = \frac{1}{{25}}\left( {1.18,{5^2} + 6.19,{5^2} + 8.20,{5^2} + 7.21,{5^2} + 2.22,{5^2} + 1.23,{5^2}} \right) - 20,{74^2} = 1,3024\)
Độ lệch chuẩn: \({s_1} = \sqrt {1,3024} = \frac{{\sqrt {814} }}{{25}}\)
Hệ số biến thiên: \(c{v_1} = \frac{{{s_1}}}{{\overline {{x_1}} }} = \frac{{\frac{{\sqrt {814} }}{{25}}}}{{20,74}} \approx 0,055\)
Chiều dài gang tay của học sinh nữ:
Phương sai:
\(s_2^2 = \frac{1}{{20}}\left( {16,{5^2}.3 + 17,{5^2}.2 + 18,{5^2}.8 + 19,{5^2}.4 + 20,{5^2}.2 + 21,{5^2}.1} \right) - 18,{65^2} = 1,7275\)
Độ lệch chuẩn: \({s_2} = \sqrt {1,7275} = \frac{{\sqrt {691} }}{{20}}\)
Hệ số biến thiên: \(c{v_2} = \frac{{{s_2}}}{{\overline {{x_2}} }} = \frac{{\frac{{\sqrt {691} }}{{20}}}}{{18,65}} \approx 0,07\)
Vì \(c{v_1} < c{v_2}\) nên chiều dài gang tay học sinh nữ phân tán nhiều hơn chiều dài gang tay học sinh nam trong lớp.
Trả lời câu hỏi Hoạt động 2 trang 95 SGK Toán 12 Kết nối tri thức
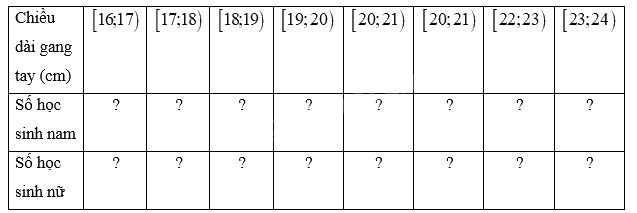
Lập bảng tần số ghép nhóm cho dữ liệu thu được trên từng nhóm theo mẫu sau đây và minh họa bằng biểu đồ tần số.
Phương pháp giải:
Sử dụng kiến thức về lập bảng tần số ghép nhóm cho dữ liệu và vẽ biểu đồ để thực hiện.
Lời giải chi tiết:
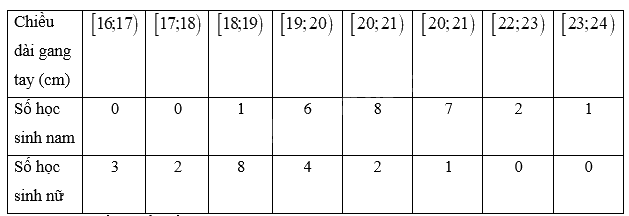
Minh họa bằng biểu đồ:
+ Biểu đồ thể hiện tần số chiều dài gang tay của các học sinh nam:
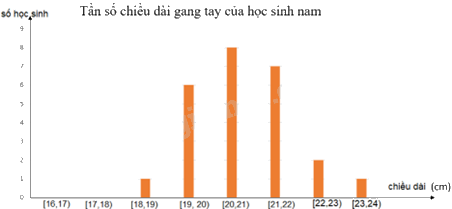
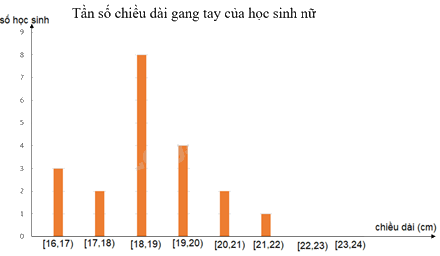
+ Biểu đồ thể hiện tần số chiều dài gang tay của các học sinh nữ:
Trả lời câu hỏi Hoạt động 2 trang 95 SGK Toán 12 Kết nối tri thức
Lập bảng tần số ghép nhóm cho dữ liệu thu được trên từng nhóm theo mẫu sau đây và minh họa bằng biểu đồ tần số.
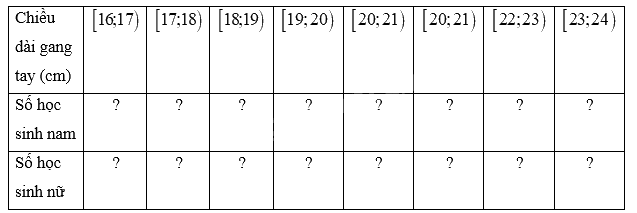
Phương pháp giải:
Sử dụng kiến thức về lập bảng tần số ghép nhóm cho dữ liệu và vẽ biểu đồ để thực hiện.
Lời giải chi tiết:
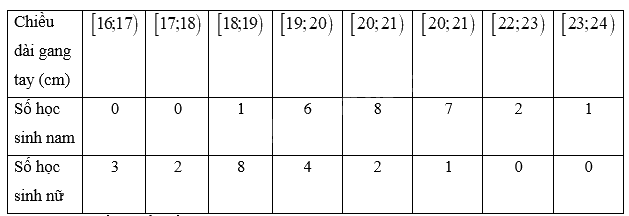
Minh họa bằng biểu đồ:
+ Biểu đồ thể hiện tần số chiều dài gang tay của các học sinh nam:
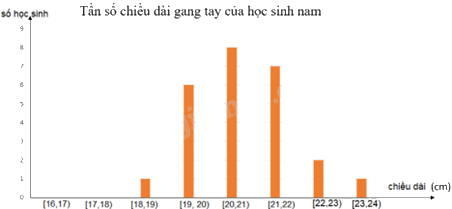
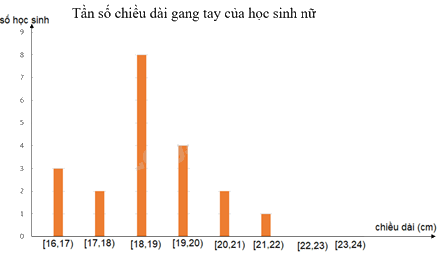
+ Biểu đồ thể hiện tần số chiều dài gang tay của các học sinh nữ:
Trả lời câu hỏi Hoạt động 3 trang 95 SGK Toán 12 Kết nối tri thức
Sử dụng bảng tần số thu được ở HĐ2, em hãy:
a) Tính độ gang tay trung bình của các học sinh nữ, học sinh nam trong lớp và so sánh.
b) Tính phương sai và độ lệch chuẩn và từ đó tính hệ số biến thiên độ dài gang tay của hai nhóm học sinh này và so sánh.
Phương pháp giải:
Sử dụng kiến thức về phương sai của mẫu số liệu ghép nhóm để tính: Phương sai của mẫu số liệu ghép nhóm, kí hiệu là \({s^2}\), là một số được tính theo công thức sau: \({s^2} = \frac{1}{n}\left( {{m_1}x_1^2 + ... + {m_k}x_k^2} \right) - {\left( {\overline x } \right)^2}\), trong đó với là số trung bình của mẫu số liệu ghép nhóm.
Sử dụng kiến thức độ lệch chuẩn của mẫu số liệu ghép nhóm để tính: Độ lệch chuẩn của mẫu số liệu ghép nhóm, kí hiệu là s, là căn bậc \(n = {m_1} + ... + {m_k}\)hai số học của phương sai của mẫu số liệu ghép nhóm, tức là \(s = \sqrt {{s^2}} \)
Sử dụng kiến thức về hệ số biến thiên để tính hệ số biến thiên độ dài gang tay: Hệ số biến thiên tính theo công thức: \(cv = \frac{s}{{\overline x }}\), trong đó: s là độ lệch chuẩn của mẫu số liệu, \(\overline x \) là giá trị trung bình của mẫu số liệu
Lời giải chi tiết:
a) Bảng số liệu với giá trị đại diện
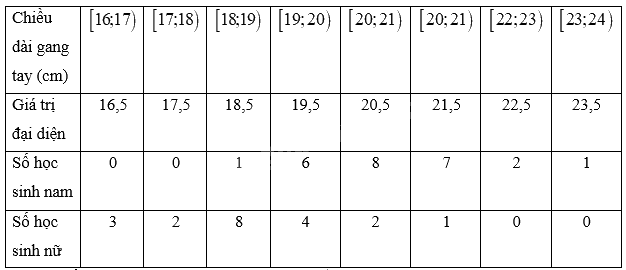
Chiều dài gang tay trung bình của học sinh nam trong lớp là:
\(\overline {{x_1}} = \frac{{18,5.1 + 19,5.6 + 20,5.8 + 21,5.7 + 22,5.2 + 23,5.1}}{{1 + 6 + 8 + 7 + 2 + 1}} = 20,74\left( {cm} \right)\)
Chiều dài gang tay trung bình của học sinh nữ trong lớp là:
\(\overline {{x_2}} = \frac{{16,5.3 + 17,5.2 + 18,5.8 + 19,5.4 + 20,5.2 + 21,5.1}}{{3 + 2 + 8 + 4 + 2 + 1}} = 18,65\left( {cm} \right)\)
b) Chiều dài gang tay của học sinh nam:
Phương sai:
\(s_1^2 = \frac{1}{{25}}\left( {1.18,{5^2} + 6.19,{5^2} + 8.20,{5^2} + 7.21,{5^2} + 2.22,{5^2} + 1.23,{5^2}} \right) - 20,{74^2} = 1,3024\)
Độ lệch chuẩn: \({s_1} = \sqrt {1,3024} = \frac{{\sqrt {814} }}{{25}}\)
Hệ số biến thiên: \(c{v_1} = \frac{{{s_1}}}{{\overline {{x_1}} }} = \frac{{\frac{{\sqrt {814} }}{{25}}}}{{20,74}} \approx 0,055\)
Chiều dài gang tay của học sinh nữ:
Phương sai:
\(s_2^2 = \frac{1}{{20}}\left( {16,{5^2}.3 + 17,{5^2}.2 + 18,{5^2}.8 + 19,{5^2}.4 + 20,{5^2}.2 + 21,{5^2}.1} \right) - 18,{65^2} = 1,7275\)
Độ lệch chuẩn: \({s_2} = \sqrt {1,7275} = \frac{{\sqrt {691} }}{{20}}\)
Hệ số biến thiên: \(c{v_2} = \frac{{{s_2}}}{{\overline {{x_2}} }} = \frac{{\frac{{\sqrt {691} }}{{20}}}}{{18,65}} \approx 0,07\)
Vì \(c{v_1} < c{v_2}\) nên chiều dài gang tay học sinh nữ phân tán nhiều hơn chiều dài gang tay học sinh nam trong lớp.
Trả lời câu hỏi Hoạt động 4 trang 95 SGK Toán 12 Kết nối tri thức
Bảng tần số sau đây là dữ liệu thu được trên một lớp học. Hãy thực hiện HĐ3 cho mẫu số liệu này.
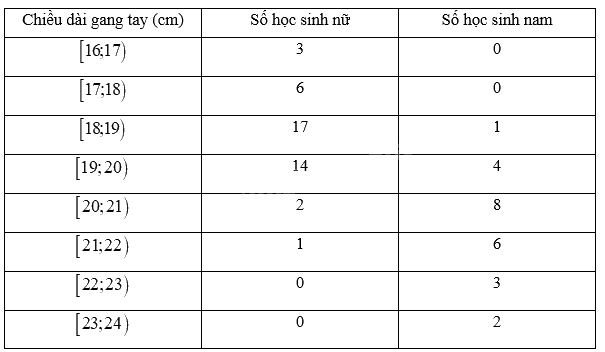
Phương pháp giải:
Sử dụng kiến thức về phương sai của mẫu số liệu ghép nhóm để tính: Phương sai của mẫu số liệu ghép nhóm, kí hiệu là \({s^2}\), là một số được tính theo công thức sau: \({s^2} = \frac{1}{n}\left( {{m_1}x_1^2 + ... + {m_k}x_k^2} \right) - {\left( {\overline x } \right)^2}\), trong đó \(n = {m_1} + ... + {m_k}\) với \(\overline x = \frac{{{m_1}{x_1} + ... + {m_k}{x_k}}}{n}\) là số trung bình của mẫu số liệu ghép nhóm.
Sử dụng kiến thức độ lệch chuẩn của mẫu số liệu ghép nhóm để tính: Độ lệch chuẩn của mẫu số liệu ghép nhóm, kí hiệu là s, là căn bậc hai số học của phương sai của mẫu số liệu ghép nhóm, tức là \(s = \sqrt {{s^2}} \)
Sử dụng kiến thức về hệ số biến thiên để tính hệ số biến thiên độ dài gang tay: Hệ số biến thiên tính theo công thức: \(cv = \frac{s}{{\overline x }}\), trong đó: s là độ lệch chuẩn của mẫu số liệu, \(\overline x \) là giá trị trung bình của mẫu số liệu
Lời giải chi tiết:
a) Bảng số liệu với giá trị đại diện
Chiều dài gang tay trung bình của học sinh nam trong lớp là:
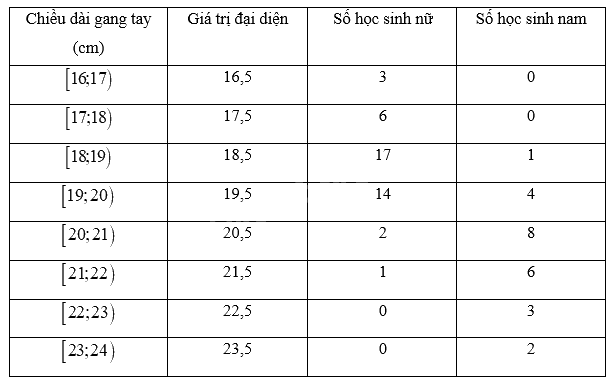
\(\overline {{x_1}} = \frac{{18,5.1 + 19,5.4 + 20,5.8 + 21,5.6 + 22,5.3 + 23,5.2}}{{1 + 4 + 8 + 6 + 3 + 2}} = 21\left( {cm} \right)\)
Chiều dài gang tay trung bình của học sinh nữ trong lớp là:
\(\overline {{x_2}} = \frac{{16,5.3 + 17,5.6 + 18,5.17 + 19,5.14 + 20,5.2 + 21,5.1}}{{3 + 6 + 17 + 14 + 2 + 1}} = \frac{{1609}}{{86}}\left( {cm} \right)\)
b) Chiều dài gang tay của học sinh nam có:
Phương sai:
\(s_1^2 = \frac{1}{{24}}\left( {1.18,{5^2} + 4.19,{5^2} + 8.20,{5^2} + 6.21,{5^2} + 3.22,{5^2} + 2.23,{5^2}} \right) - {21^2} = \frac{{19}}{{12}}\)
Độ lệch chuẩn: \({s_1} = \sqrt {\frac{{19}}{{12}}} = \frac{{\sqrt {57} }}{6}\)
Hệ số biến thiên: \(c{v_1} = \frac{{{s_1}}}{{\overline {{x_1}} }} = \frac{{\frac{{\sqrt {57} }}{6}}}{{21}} \approx 0,0599\)
Chiều dài gang tay của học sinh nữ có:
Phương sai:
\(s_2^2 = \frac{1}{{43}}\left( {16,{5^2}.3 + 17,{5^2}.6 + 18,{5^2}.17 + 19,{5^2}.14 + 20,{5^2}.2 + 21,{5^2}.1} \right) - {\left( {\frac{{1609}}{{86}}} \right)^2} \approx 1,1\)
Độ lệch chuẩn: \({s_2} = \sqrt {1,1} \approx 1,05\)
Hệ số biến thiên: \(c{v_2} = \frac{{{s_2}}}{{\overline {{x_2}} }} = \frac{{1,05}}{{\frac{{1609}}{{86}}}} \approx 0,0561\)
Vì \(c{v_1} > c{v_2}\) nên độ dài gang tay học sinh nam phân tán nhiều hơn độ dài gang tay học sinh nữ trong lớp.
Mục 2 trang 95 SGK Toán 12 tập 1 - Kết nối tri thức tập trung vào việc ôn tập và củng cố kiến thức về đạo hàm. Đây là một trong những chủ đề quan trọng nhất của chương trình Toán 12, đóng vai trò nền tảng cho việc giải quyết các bài toán phức tạp hơn trong các chương tiếp theo. Để giải quyết tốt các bài tập trong mục này, học sinh cần nắm vững các khái niệm cơ bản về đạo hàm, các quy tắc tính đạo hàm và các ứng dụng của đạo hàm trong việc tìm cực trị, khảo sát hàm số.
Dưới đây là hướng dẫn giải chi tiết các bài tập trong mục 2 trang 95 SGK Toán 12 tập 1 - Kết nối tri thức:
Để tính đạo hàm của một hàm số, ta cần áp dụng các quy tắc tính đạo hàm đã học. Ví dụ, để tính đạo hàm của hàm số f(x) = x2 + 2x + 1, ta áp dụng quy tắc tính đạo hàm của hàm số đa thức:
f'(x) = 2x + 2
Để tìm đạo hàm của hàm số y = sin(x)cos(x), ta áp dụng quy tắc tính đạo hàm của hàm hợp:
y' = cos(x)cos(x) + sin(x)(-sin(x)) = cos2(x) - sin2(x) = cos(2x)
Để tìm đạo hàm của hàm số y = exln(x), ta áp dụng quy tắc tính đạo hàm của tích hai hàm số:
y' = exln(x) + ex(1/x) = ex(ln(x) + 1/x)
Trong mục 2 trang 95 SGK Toán 12 tập 1 - Kết nối tri thức, học sinh thường gặp các dạng bài tập sau:
Để giải quyết tốt các dạng bài tập này, học sinh cần luyện tập thường xuyên và nắm vững các kiến thức cơ bản về đạo hàm. Ngoài ra, việc sử dụng các công cụ hỗ trợ như máy tính bỏ túi hoặc phần mềm giải toán cũng có thể giúp học sinh tiết kiệm thời gian và công sức.
Để học tập và ôn luyện hiệu quả môn Toán 12, đặc biệt là phần đạo hàm, học sinh nên:
Chúc các bạn học tập tốt và đạt kết quả cao trong môn Toán 12!