Giải bài tập 2.36 trang 74 SGK Toán 12 tập 1 - Kết nối tri thức

Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 12. Bài viết này sẽ hướng dẫn bạn cách giải bài tập 2.36 trang 74 SGK Toán 12 tập 1 - Kết nối tri thức một cách nhanh chóng và hiệu quả.

Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp bạn nắm vững kiến thức và đạt kết quả cao trong môn Toán.

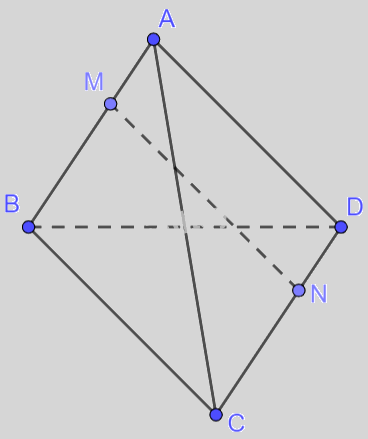
Cho tứ diện ABCD, lấy hai điểm M, N thỏa mãn (overrightarrow {MB} + 2overrightarrow {MA} = overrightarrow 0 ) và (overrightarrow {NC} = 2overrightarrow {DN} ). Hãy biểu diễn (overrightarrow {MN} ) theo (overrightarrow {AD} ) và (overrightarrow {BC} ).

Đề bài

Cho tứ diện ABCD, lấy hai điểm M, N thỏa mãn \(\overrightarrow {MB} + 2\overrightarrow {MA} = \overrightarrow 0 \) và \(\overrightarrow {NC} = 2\overrightarrow {DN} \). Hãy biểu diễn \(\overrightarrow {MN} \) theo \(\overrightarrow {AD} \) và \(\overrightarrow {BC} \).

Phương pháp giải - Xem chi tiết Giải bài tập 2.36 trang 74 SGK Toán 12 tập 1 - Kết nối tri thức 1

Sử dụng kiến thức về quy tắc ba điểm để chứng minh: Nếu A, B, C là ba điểm bất kì thì \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)

Lời giải chi tiết

Giải bài tập 2.36 trang 74 SGK Toán 12 tập 1 - Kết nối tri thức 2

Ta có: \(\overrightarrow {MB} + 2\overrightarrow {MA} = \overrightarrow 0 \Rightarrow \overrightarrow {MB} = - 2\overrightarrow {MA} ,\overrightarrow {NC} = 2\overrightarrow {DN} \Rightarrow \overrightarrow {CN} = - 2\overrightarrow {DN} \)

Ta có: \(\overrightarrow {MN} = \overrightarrow {MA} + \overrightarrow {AD} + \overrightarrow {DN} \) (1)

\(\overrightarrow {MN} = \overrightarrow {MB} + \overrightarrow {BC} + \overrightarrow {CN} = - 2\overrightarrow {MA} + \overrightarrow {BC} - 2\overrightarrow {DN} \) (2)

Cộng vế với vế của (1) và (2) ta có:

\(2\overrightarrow {MN} = \overrightarrow {MA} + \overrightarrow {AD} + \overrightarrow {DN} - 2\overrightarrow {MA} + \overrightarrow {BC} - 2\overrightarrow {DN} = - \overrightarrow {MA} - \overrightarrow {DN} + \overrightarrow {BC} + \overrightarrow {AD} \)

\( = \frac{1}{3}\overrightarrow {AB} + \frac{1}{3}\overrightarrow {CD} + \overrightarrow {BC} + \overrightarrow {AD} = \frac{1}{3}\left( {\overrightarrow {AC} + \overrightarrow {CB} + \overrightarrow {CA} + \overrightarrow {AD} } \right) + \overrightarrow {BC} + \overrightarrow {AD} = \frac{2}{3}\overrightarrow {BC} + \frac{4}{3}\overrightarrow {AD} \)

\(\overrightarrow {MN} = \frac{1}{3}\overrightarrow {BC} + \frac{2}{3}\overrightarrow {AD} \)

Tự tin bứt phá Kỳ thi THPT Quốc gia môn Toán! Đừng bỏ lỡ Giải bài tập 2.36 trang 74 SGK Toán 12 tập 1 - Kết nối tri thức đặc sắc thuộc chuyên mục giải sgk toán 12 trên nền tảng toán học. Với bộ bài tập toán thpt được biên soạn chuyên sâu, bám sát cấu trúc đề thi và chương trình Toán 12, đây chính là "chiến lược vàng" giúp các em tối ưu hóa ôn luyện. Học sinh sẽ không chỉ làm chủ mọi dạng bài thi mà còn nắm vững chiến thuật làm bài hiệu quả, sẵn sàng tự tin chinh phục điểm cao, vững bước vào đại học mơ ước nhờ phương pháp học trực quan, khoa học và hiệu quả học tập vượt trội!

Giải bài tập 2.36 trang 74 SGK Toán 12 tập 1 - Kết nối tri thức: Hướng dẫn chi tiết

Bài tập 2.36 trang 74 SGK Toán 12 tập 1 - Kết nối tri thức thuộc chương trình học về đạo hàm. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm của hàm số để giải quyết các bài toán thực tế. Dưới đây là hướng dẫn chi tiết cách giải bài tập này:

Phân tích đề bài

Trước khi bắt đầu giải bài tập, chúng ta cần phân tích đề bài để xác định rõ yêu cầu và các thông tin đã cho. Bài tập 2.36 thường liên quan đến việc tìm đạo hàm của một hàm số tại một điểm cụ thể, hoặc tìm điều kiện để hàm số có đạo hàm tại một điểm. Đề bài có thể yêu cầu sử dụng các quy tắc tính đạo hàm đã học, như quy tắc đạo hàm của tổng, hiệu, tích, thương, hàm hợp, và các đạo hàm cơ bản.

Các bước giải bài tập

Bước 1: Xác định hàm số và điểm cần tính đạo hàm. Đọc kỹ đề bài để xác định chính xác hàm số f(x) và điểm x₀ mà tại đó cần tính đạo hàm f'(x₀).
Bước 2: Áp dụng quy tắc tính đạo hàm. Sử dụng các quy tắc đạo hàm đã học để tính đạo hàm của hàm số f(x). Nếu hàm số phức tạp, có thể cần chia nhỏ thành các bước nhỏ hơn để tính đạo hàm từng phần.
Bước 3: Thay giá trị x₀ vào đạo hàm. Sau khi tính được đạo hàm f'(x), thay giá trị x₀ vào để tìm đạo hàm tại điểm đó, f'(x₀).
Bước 4: Kiểm tra kết quả. Đảm bảo rằng kết quả tính được phù hợp với yêu cầu của đề bài và không có sai sót trong quá trình tính toán.

Ví dụ minh họa

Giả sử đề bài yêu cầu tính đạo hàm của hàm số f(x) = x² + 2x + 1 tại điểm x = 1.

Bước 1: Hàm số f(x) = x² + 2x + 1, điểm x₀ = 1.
Bước 2: Tính đạo hàm f'(x) = 2x + 2 (sử dụng quy tắc đạo hàm của tổng và đạo hàm của xⁿ).
Bước 3: Thay x = 1 vào đạo hàm: f'(1) = 2(1) + 2 = 4.
Bước 4: Kết quả: Đạo hàm của hàm số f(x) tại điểm x = 1 là 4.

Lưu ý quan trọng

Nắm vững các quy tắc tính đạo hàm cơ bản.
Thực hành giải nhiều bài tập để làm quen với các dạng bài khác nhau.
Kiểm tra kỹ kết quả trước khi kết luận.
Sử dụng máy tính bỏ túi hoặc phần mềm tính toán để kiểm tra lại kết quả.

Mở rộng kiến thức

Ngoài việc giải bài tập 2.36, bạn nên tìm hiểu thêm về các ứng dụng của đạo hàm trong thực tế, như tìm cực trị của hàm số, khảo sát hàm số, và giải các bài toán tối ưu hóa. Việc hiểu rõ các ứng dụng này sẽ giúp bạn nắm vững kiến thức và áp dụng vào giải quyết các vấn đề thực tế.

Tổng kết

Bài tập 2.36 trang 74 SGK Toán 12 tập 1 - Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm. Bằng cách phân tích đề bài, áp dụng các quy tắc tính đạo hàm, và kiểm tra kết quả, bạn có thể giải quyết bài tập này một cách hiệu quả. Chúc bạn học tập tốt!