Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 tập 1 của giaitoan.edu.vn. Ở bài viết này, chúng ta sẽ cùng nhau giải chi tiết các bài tập trong mục 2 trang 49, 50, 51 sách giáo khoa Toán 12 tập 1 - Kết nối tri thức.
Mục tiêu của chúng tôi là cung cấp cho các em những lời giải chính xác, dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Tổng và hiệu của hai vectơ trong không gian
Trả lời câu hỏi Luyện tập 3 trang 50 SGK Toán 12 Kết nối tri thức
Trong Ví dụ 3, hãy tính độ dài của vectơ \(\overrightarrow {AC} + \overrightarrow {C'D'} \).
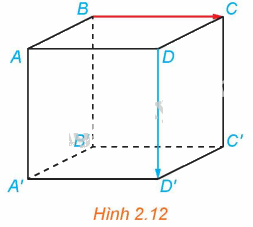
Ví dụ 3: Cho hình lập phương ABCD.A’B’C’D’ có độ dài mỗi cạnh bằng 1 (H.2.12).
Phương pháp giải:
Sử dụng kiến thức về quy tắc ba điểm để tính: Nếu A, B, C là ba điểm bất kì thì \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
Lời giải chi tiết:
Vì ABCD.A’B’C’D’ là hình lập phương nên DCC’D’ là hình vuông. Do đó, \(\overrightarrow {C'D'} = \overrightarrow {CD} \).
Ta có: \(\overrightarrow {AC} + \overrightarrow {C'D'} = \overrightarrow {AC} + \overrightarrow {CD} = \overrightarrow {AD} \)
Vì độ dài mỗi cạnh hình lập phương ABCD.A’B’C’D’ bằng 1 nên \(\left| {\overrightarrow {AD} } \right| = 1\).
Vậy \(\left| {\overrightarrow {AC} + \overrightarrow {C'D'} } \right| = 1\)
Trả lời câu hỏi Luyện tập 4 trang 50SGK Toán 12 Kết nối tri thức
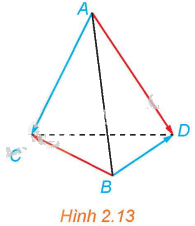
Cho tứ diện ABCD (H.2.13). Chứng minh rằng \(\overrightarrow {AB} + \overrightarrow {CD} = \overrightarrow {AD} + \overrightarrow {CB} \).
Phương pháp giải:
Sử dụng kiến thức về quy tắc ba điểm để tính: Nếu A, B, C là ba điểm bất kì thì \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
Lời giải chi tiết:
Ta có: \(\overrightarrow {AB} + \overrightarrow {CD} = \overrightarrow {AD} + \overrightarrow {DB} + \overrightarrow {CB} + \overrightarrow {BD} = \left( {\overrightarrow {AD} + \overrightarrow {CB} } \right) + \left( {\overrightarrow {DB} + \overrightarrow {BD} } \right)\)
\( = \overrightarrow {AD} + \overrightarrow {CB} + \overrightarrow {DD} = \overrightarrow {AD} + \overrightarrow {CB} \) (đpcm)
Trả lời câu hỏi Hoạt động 3 trang 49SGK Toán 12 Kết nối tri thức
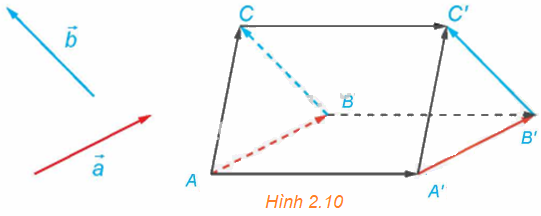
Trong không gian, cho hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) không cùng phương. Lấy điểm A và vẽ các vectơ \(\overrightarrow {AB} = \overrightarrow a ,\overrightarrow {BC} = \overrightarrow b \). Lấy điểm A’ và vẽ các vectơ \(\overrightarrow {A'B'} = \overrightarrow a ,\overrightarrow {B'C'} = \overrightarrow b \) (H.2.10).
a) Giải thích vì sao \(\overrightarrow {AA'} = \overrightarrow {BB'} \) và \(\overrightarrow {BB'} = \overrightarrow {CC'} \).
b) Giải thích vì sao AA’C’C là hình bình hành, từ đó suy ra \(\overrightarrow {AC} = \overrightarrow {A'C'} \).
Phương pháp giải:
Sử dụng kiến thức về hai vectơ bằng nhau để giải thích: Hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) được gọi là bằng nhau, kí hiệu \(\overrightarrow a = \overrightarrow b \), nếu chúng có cùng độ dài và cùng hướng.
Lời giải chi tiết:
a) Vì \(\overrightarrow {AB} = \overrightarrow a \) nên hai vectơ \(\overrightarrow a \) và \(\overrightarrow {AB} \) cùng hướng và cùng độ dài.
Vì \(\overrightarrow {A'B'} = \overrightarrow a \) nên hai vectơ \(\overrightarrow a \) và \(\overrightarrow {A'B'} \) cùng hướng và cùng độ dài.
Do đó, hai vectơ \(\overrightarrow {A'B'} \) và \(\overrightarrow {AB} \) cùng hướng và cùng độ dài. Suy ra, AB//A’B’ và \(AB = A'B'\). Do đó, tứ giác ABB’A’ là hình bình hành. Suy ra, AA’//BB’ và \(AA' = BB' \Rightarrow \) hai vectơ \(\overrightarrow {AA'} ,\overrightarrow {BB'} \) có cùng hướng và cùng độ dài. Suy ra, \(\overrightarrow {AA'} = \overrightarrow {BB'} \).
Vì \(\overrightarrow {BC} = \overrightarrow b \) nên hai vectơ \(\overrightarrow b \) và \(\overrightarrow {BC} \) cùng hướng và cùng độ dài.
Vì \(\overrightarrow {B'C'} = \overrightarrow b \) nên hai vectơ \(\overrightarrow b \) và \(\overrightarrow {B'C'} \) cùng hướng và cùng độ dài.
Do đó, hai vectơ \(\overrightarrow {BC} \) và \(\overrightarrow {B'C'} \) cùng hướng và cùng độ dài. Suy ra, BC//B’C’ và \(BC = B'C'\). Do đó, tứ giác CBB’C’ là hình bình hành. Suy ra, CC’//BB’ và \(CC' = BB' \Rightarrow \) hai vectơ \(\overrightarrow {BB'} ,\overrightarrow {CC'} \) có cùng hướng và cùng độ dài. Suy ra, \(\overrightarrow {BB'} = \overrightarrow {CC'} \).
b) Vì hai vectơ \(\overrightarrow {AA'} ,\overrightarrow {BB'} \) có cùng hướng và cùng độ dài; hai vectơ \(\overrightarrow {BB'} ,\overrightarrow {CC'} \) có cùng hướng và cùng độ dài nên hai vectơ \(\overrightarrow {AA'} \) và \(\overrightarrow {CC'} \) có cùng hướng và cùng độ dài. Do đó, AA’//CC’ và \(AA' = CC'\) nên tứ giác AA’C’C là hình bình hành. Suy ra, \(AC = A'C'\) và AC//A’C’. Do đó, hai vectơ \(\overrightarrow {AC} ,\overrightarrow {A'C'} \) có cùng hướng và cùng độ dài. Suy ra, \(\overrightarrow {AC} = \overrightarrow {A'C'} \).
Trả lời câu hỏi Luyện tập 6 trang 52SGK Toán 12 Kết nối tri thức
Trong Ví dụ 6, chứng minh rằng:
a) \(\overrightarrow {BN} \) và \(\overrightarrow {DM} \) là hai vectơ đối nhau;
b) \(\overrightarrow {SD} - \overrightarrow {BN} - \overrightarrow {CM} = \overrightarrow {SC} \)
Phương pháp giải:
a) Sử dụng kiến thức về hai vectơ đối nhau để chứng minh: Trong không gian, vectơ có cùng độ dài và ngược hướng với vectơ \(\overrightarrow a \) được gọi là vectơ đối của vectơ \(\overrightarrow a \), kí hiệu là \( - \overrightarrow a \).
b) Sử dụng kiến thức về quy tắc ba điểm để chứng minh: Nếu A, B, C là ba điểm bất kì thì \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
Lời giải chi tiết:
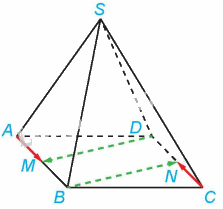
a) Tứ giác ABCD là hình bình hành nên \(AB = CD\), AB//CD. Suy ra \(BM = DN\) (vì M, N lần lượt là trung điểm của AB và CD) và BM//DN. Do đó, tứ giác DMBN là hình bình hành, do đó, \(BN = DM\) và BN//DM. Hai vectơ \(\overrightarrow {BN} \) và \(\overrightarrow {DM} \) có cùng độ dài và ngược hướng nên \(\overrightarrow {BN} \) và \(\overrightarrow {DM} \) là hai vectơ đối nhau.
b) Theo a ta có: \(\overrightarrow {BN} = - \overrightarrow {DM} \)
Do đó, \(\overrightarrow {SD} - \overrightarrow {BN} - \overrightarrow {CM} = \overrightarrow {SD} + \overrightarrow {DM} + \overrightarrow {MC} = \overrightarrow {SM} + \overrightarrow {MC} = \overrightarrow {SC} \)
Trả lời câu hỏi Luyện tập 5 trang 50SGK Toán 12 Kết nối tri thức
Cho hình hộp hình chữ nhật ABCD.A’B’C’D’. Chứng minh rằng \(\overrightarrow {BB'} + \overrightarrow {CD} + \overrightarrow {AD} = \overrightarrow {BD'} \)
Phương pháp giải:
Sử dụng kiến thức về quy tắc hình hộp để giải: Cho hình hộp ABCD.A’B’C’D’. Khi đó, ta có: \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AC'} \).
Lời giải chi tiết:
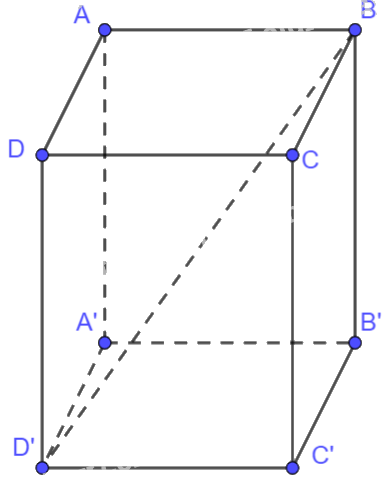
Vì ABCD là hình chữ nhật nên \(\overrightarrow {AD} = \overrightarrow {BC} ,\overrightarrow {CD} = \overrightarrow {BA} \)
Vì ABCD.A’B’C’D’ là hình hộp chữ nhật nên \(\overrightarrow {BB'} + \overrightarrow {BA} + \overrightarrow {BC} = \overrightarrow {BD'} \)
Ta có: \(\overrightarrow {BB'} + \overrightarrow {CD} + \overrightarrow {AD} = \overrightarrow {BB'} + \overrightarrow {BA} + \overrightarrow {BC} = \overrightarrow {BD'} \)
Trả lời câu hỏi Câu hỏi trang 50SGK Toán 12 Kết nối tri thức
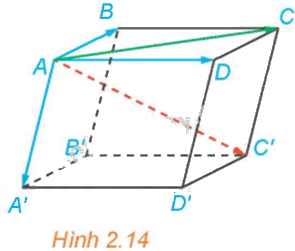
Trong Hình 2.14, hãy phát biểu quy tắc hình hộp với các vectơ có điểm đầu là B.
Phương pháp giải:
Sử dụng kiến thức về quy tắc hình hộp để giải bài toán: Cho hình hộp ABCD.A’B’C’D’. Khi đó, ta có: \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AC'} \)
Lời giải chi tiết:
Quy tắc hình hộp với các vectơ có điểm đầu là B là: \(\overrightarrow {BA} + \overrightarrow {BC} + \overrightarrow {BB'} = \overrightarrow {BD'} \)
Trả lời câu hỏi Hoạt động 4 trang 50SGK Toán 12 Kết nối tri thức
Cho hình hộp ABCD.A’B’C’D’ (H.2.14).
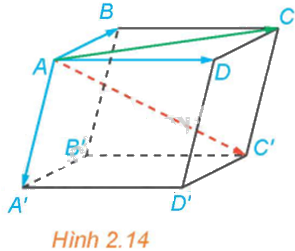
a) Hai vectơ \(\overrightarrow {AB} + \overrightarrow {AD} \) và \(\overrightarrow {AC} \) có bằng nhau hay không?
b) Hai vectơ \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} \) và \(\overrightarrow {AC'} \) có bằng nhau hay không?
Phương pháp giải:
Sử dụng quy tắc hình bình hành để chứng minh: Nếu ABCD là hình bình hành thì \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)
Lời giải chi tiết:
a) Vì ABCD là hình bình hành nên \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)
b) Ta có: \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AC} + \overrightarrow {AA'} \) (1)
Vì ABCD. A’B’C’D’ là hình hộp nên AA’D’D và DD’C’C là hình bình hành. Do đó, AA’//DD’, \(AA' = DD'\) và \(DD' = CC'\), DD’//CC’. Suy ra, AA’//CC’ và \(AA' = CC'\). Suy ra, tứ giác AA’C’C là hình bình hành. Suy ra: \(\overrightarrow {AC} + \overrightarrow {AA'} = \overrightarrow {AC'} \) (2)
Từ (1) và (2) ta có: \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AC'} \)
Trả lời câu hỏi Hoạt động 5 trang 51SGK Toán 12 Kết nối tri thức
Hình 2.15 mô tả một lọ hoa được đặt trên bàn, trọng lượng của lọ hoa tạo nên một lực tác dụng lên mặt bàn và một phản lực từ mặt bàn lên lọ hoa. Có nhận xét về độ dài và hướng của các vectơ biểu diễn hai lực đó.

Phương pháp giải:
Sử dụng kiến thức về Định luật III Newton để giải thích: Lực tác dụng và phản lực là hai lực cùng phương, ngược hướng và có độ lớn bằng nhau.
Lời giải chi tiết:
Các vectơ biểu diễn hai lực đó có độ dài bằng nhau và hướng của chúng là ngược nhau.
Trả lời câu hỏi Vận dụng 2 trang 52SGK Toán 12 Kết nối tri thức
Thang cuốn tại các trung tâm thương mại, siêu thị hay nhà ga, sân bay thường có hai làn, trong đó một làn lên và một làn xuống. Khi thang cuốn chuyển động, vectơ biểu diễn vận tốc của mỗi làn có là hai vectơ đối nhau không? Giải thích vì sao.

Phương pháp giải:
Sử dụng kiến thức về hai vectơ đối nhau để giải thích: Trong không gian, vectơ có cùng độ dài và ngược hướng với vectơ \(\overrightarrow a \) được gọi là vectơ đối của vectơ \(\overrightarrow a \), kí hiệu là \( - \overrightarrow a \).
Lời giải chi tiết:
Vectơ biểu diễn vận tốc của mỗi làn có cùng độ lớn và hướng ngược nhau nên chúng là hai vectơ đối nhau.
Trả lời câu hỏi Hoạt động 3 trang 49SGK Toán 12 Kết nối tri thức
Trong không gian, cho hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) không cùng phương. Lấy điểm A và vẽ các vectơ \(\overrightarrow {AB} = \overrightarrow a ,\overrightarrow {BC} = \overrightarrow b \). Lấy điểm A’ và vẽ các vectơ \(\overrightarrow {A'B'} = \overrightarrow a ,\overrightarrow {B'C'} = \overrightarrow b \) (H.2.10).
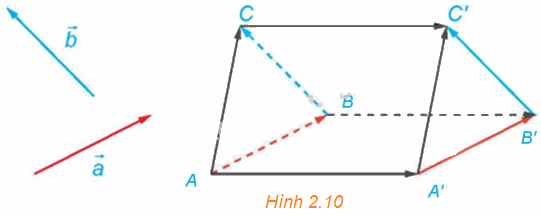
a) Giải thích vì sao \(\overrightarrow {AA'} = \overrightarrow {BB'} \) và \(\overrightarrow {BB'} = \overrightarrow {CC'} \).
b) Giải thích vì sao AA’C’C là hình bình hành, từ đó suy ra \(\overrightarrow {AC} = \overrightarrow {A'C'} \).
Phương pháp giải:
Sử dụng kiến thức về hai vectơ bằng nhau để giải thích: Hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) được gọi là bằng nhau, kí hiệu \(\overrightarrow a = \overrightarrow b \), nếu chúng có cùng độ dài và cùng hướng.
Lời giải chi tiết:
a) Vì \(\overrightarrow {AB} = \overrightarrow a \) nên hai vectơ \(\overrightarrow a \) và \(\overrightarrow {AB} \) cùng hướng và cùng độ dài.
Vì \(\overrightarrow {A'B'} = \overrightarrow a \) nên hai vectơ \(\overrightarrow a \) và \(\overrightarrow {A'B'} \) cùng hướng và cùng độ dài.
Do đó, hai vectơ \(\overrightarrow {A'B'} \) và \(\overrightarrow {AB} \) cùng hướng và cùng độ dài. Suy ra, AB//A’B’ và \(AB = A'B'\). Do đó, tứ giác ABB’A’ là hình bình hành. Suy ra, AA’//BB’ và \(AA' = BB' \Rightarrow \) hai vectơ \(\overrightarrow {AA'} ,\overrightarrow {BB'} \) có cùng hướng và cùng độ dài. Suy ra, \(\overrightarrow {AA'} = \overrightarrow {BB'} \).
Vì \(\overrightarrow {BC} = \overrightarrow b \) nên hai vectơ \(\overrightarrow b \) và \(\overrightarrow {BC} \) cùng hướng và cùng độ dài.
Vì \(\overrightarrow {B'C'} = \overrightarrow b \) nên hai vectơ \(\overrightarrow b \) và \(\overrightarrow {B'C'} \) cùng hướng và cùng độ dài.
Do đó, hai vectơ \(\overrightarrow {BC} \) và \(\overrightarrow {B'C'} \) cùng hướng và cùng độ dài. Suy ra, BC//B’C’ và \(BC = B'C'\). Do đó, tứ giác CBB’C’ là hình bình hành. Suy ra, CC’//BB’ và \(CC' = BB' \Rightarrow \) hai vectơ \(\overrightarrow {BB'} ,\overrightarrow {CC'} \) có cùng hướng và cùng độ dài. Suy ra, \(\overrightarrow {BB'} = \overrightarrow {CC'} \).
b) Vì hai vectơ \(\overrightarrow {AA'} ,\overrightarrow {BB'} \) có cùng hướng và cùng độ dài; hai vectơ \(\overrightarrow {BB'} ,\overrightarrow {CC'} \) có cùng hướng và cùng độ dài nên hai vectơ \(\overrightarrow {AA'} \) và \(\overrightarrow {CC'} \) có cùng hướng và cùng độ dài. Do đó, AA’//CC’ và \(AA' = CC'\) nên tứ giác AA’C’C là hình bình hành. Suy ra, \(AC = A'C'\) và AC//A’C’. Do đó, hai vectơ \(\overrightarrow {AC} ,\overrightarrow {A'C'} \) có cùng hướng và cùng độ dài. Suy ra, \(\overrightarrow {AC} = \overrightarrow {A'C'} \).
Trả lời câu hỏi Luyện tập 3 trang 50 SGK Toán 12 Kết nối tri thức
Trong Ví dụ 3, hãy tính độ dài của vectơ \(\overrightarrow {AC} + \overrightarrow {C'D'} \).
Ví dụ 3: Cho hình lập phương ABCD.A’B’C’D’ có độ dài mỗi cạnh bằng 1 (H.2.12).
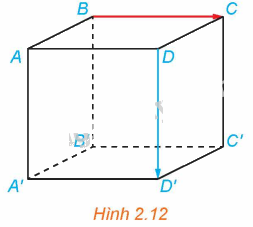
Phương pháp giải:
Sử dụng kiến thức về quy tắc ba điểm để tính: Nếu A, B, C là ba điểm bất kì thì \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
Lời giải chi tiết:
Vì ABCD.A’B’C’D’ là hình lập phương nên DCC’D’ là hình vuông. Do đó, \(\overrightarrow {C'D'} = \overrightarrow {CD} \).
Ta có: \(\overrightarrow {AC} + \overrightarrow {C'D'} = \overrightarrow {AC} + \overrightarrow {CD} = \overrightarrow {AD} \)
Vì độ dài mỗi cạnh hình lập phương ABCD.A’B’C’D’ bằng 1 nên \(\left| {\overrightarrow {AD} } \right| = 1\).
Vậy \(\left| {\overrightarrow {AC} + \overrightarrow {C'D'} } \right| = 1\)
Trả lời câu hỏi Luyện tập 4 trang 50SGK Toán 12 Kết nối tri thức
Cho tứ diện ABCD (H.2.13). Chứng minh rằng \(\overrightarrow {AB} + \overrightarrow {CD} = \overrightarrow {AD} + \overrightarrow {CB} \).
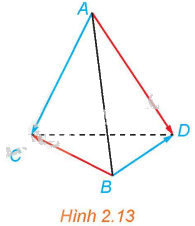
Phương pháp giải:
Sử dụng kiến thức về quy tắc ba điểm để tính: Nếu A, B, C là ba điểm bất kì thì \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
Lời giải chi tiết:
Ta có: \(\overrightarrow {AB} + \overrightarrow {CD} = \overrightarrow {AD} + \overrightarrow {DB} + \overrightarrow {CB} + \overrightarrow {BD} = \left( {\overrightarrow {AD} + \overrightarrow {CB} } \right) + \left( {\overrightarrow {DB} + \overrightarrow {BD} } \right)\)
\( = \overrightarrow {AD} + \overrightarrow {CB} + \overrightarrow {DD} = \overrightarrow {AD} + \overrightarrow {CB} \) (đpcm)
Trả lời câu hỏi Hoạt động 4 trang 50SGK Toán 12 Kết nối tri thức
Cho hình hộp ABCD.A’B’C’D’ (H.2.14).
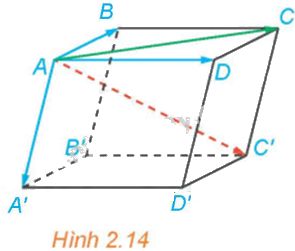
a) Hai vectơ \(\overrightarrow {AB} + \overrightarrow {AD} \) và \(\overrightarrow {AC} \) có bằng nhau hay không?
b) Hai vectơ \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} \) và \(\overrightarrow {AC'} \) có bằng nhau hay không?
Phương pháp giải:
Sử dụng quy tắc hình bình hành để chứng minh: Nếu ABCD là hình bình hành thì \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)
Lời giải chi tiết:
a) Vì ABCD là hình bình hành nên \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)
b) Ta có: \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AC} + \overrightarrow {AA'} \) (1)
Vì ABCD. A’B’C’D’ là hình hộp nên AA’D’D và DD’C’C là hình bình hành. Do đó, AA’//DD’, \(AA' = DD'\) và \(DD' = CC'\), DD’//CC’. Suy ra, AA’//CC’ và \(AA' = CC'\). Suy ra, tứ giác AA’C’C là hình bình hành. Suy ra: \(\overrightarrow {AC} + \overrightarrow {AA'} = \overrightarrow {AC'} \) (2)
Từ (1) và (2) ta có: \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AC'} \)
Trả lời câu hỏi Câu hỏi trang 50SGK Toán 12 Kết nối tri thức
Trong Hình 2.14, hãy phát biểu quy tắc hình hộp với các vectơ có điểm đầu là B.
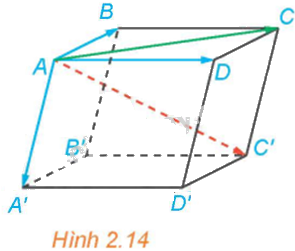
Phương pháp giải:
Sử dụng kiến thức về quy tắc hình hộp để giải bài toán: Cho hình hộp ABCD.A’B’C’D’. Khi đó, ta có: \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AC'} \)
Lời giải chi tiết:
Quy tắc hình hộp với các vectơ có điểm đầu là B là: \(\overrightarrow {BA} + \overrightarrow {BC} + \overrightarrow {BB'} = \overrightarrow {BD'} \)
Trả lời câu hỏi Luyện tập 5 trang 50SGK Toán 12 Kết nối tri thức
Cho hình hộp hình chữ nhật ABCD.A’B’C’D’. Chứng minh rằng \(\overrightarrow {BB'} + \overrightarrow {CD} + \overrightarrow {AD} = \overrightarrow {BD'} \)
Phương pháp giải:
Sử dụng kiến thức về quy tắc hình hộp để giải: Cho hình hộp ABCD.A’B’C’D’. Khi đó, ta có: \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AC'} \).
Lời giải chi tiết:
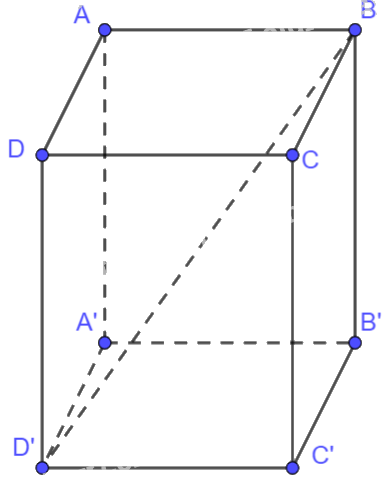
Vì ABCD là hình chữ nhật nên \(\overrightarrow {AD} = \overrightarrow {BC} ,\overrightarrow {CD} = \overrightarrow {BA} \)
Vì ABCD.A’B’C’D’ là hình hộp chữ nhật nên \(\overrightarrow {BB'} + \overrightarrow {BA} + \overrightarrow {BC} = \overrightarrow {BD'} \)
Ta có: \(\overrightarrow {BB'} + \overrightarrow {CD} + \overrightarrow {AD} = \overrightarrow {BB'} + \overrightarrow {BA} + \overrightarrow {BC} = \overrightarrow {BD'} \)
Trả lời câu hỏi Hoạt động 5 trang 51SGK Toán 12 Kết nối tri thức
Hình 2.15 mô tả một lọ hoa được đặt trên bàn, trọng lượng của lọ hoa tạo nên một lực tác dụng lên mặt bàn và một phản lực từ mặt bàn lên lọ hoa. Có nhận xét về độ dài và hướng của các vectơ biểu diễn hai lực đó.

Phương pháp giải:
Sử dụng kiến thức về Định luật III Newton để giải thích: Lực tác dụng và phản lực là hai lực cùng phương, ngược hướng và có độ lớn bằng nhau.
Lời giải chi tiết:
Các vectơ biểu diễn hai lực đó có độ dài bằng nhau và hướng của chúng là ngược nhau.
Trả lời câu hỏi Luyện tập 6 trang 52SGK Toán 12 Kết nối tri thức
Trong Ví dụ 6, chứng minh rằng:
a) \(\overrightarrow {BN} \) và \(\overrightarrow {DM} \) là hai vectơ đối nhau;
b) \(\overrightarrow {SD} - \overrightarrow {BN} - \overrightarrow {CM} = \overrightarrow {SC} \)
Phương pháp giải:
a) Sử dụng kiến thức về hai vectơ đối nhau để chứng minh: Trong không gian, vectơ có cùng độ dài và ngược hướng với vectơ \(\overrightarrow a \) được gọi là vectơ đối của vectơ \(\overrightarrow a \), kí hiệu là \( - \overrightarrow a \).
b) Sử dụng kiến thức về quy tắc ba điểm để chứng minh: Nếu A, B, C là ba điểm bất kì thì \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
Lời giải chi tiết:
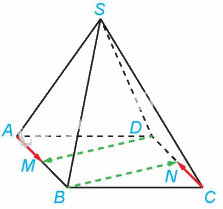
a) Tứ giác ABCD là hình bình hành nên \(AB = CD\), AB//CD. Suy ra \(BM = DN\) (vì M, N lần lượt là trung điểm của AB và CD) và BM//DN. Do đó, tứ giác DMBN là hình bình hành, do đó, \(BN = DM\) và BN//DM. Hai vectơ \(\overrightarrow {BN} \) và \(\overrightarrow {DM} \) có cùng độ dài và ngược hướng nên \(\overrightarrow {BN} \) và \(\overrightarrow {DM} \) là hai vectơ đối nhau.
b) Theo a ta có: \(\overrightarrow {BN} = - \overrightarrow {DM} \)
Do đó, \(\overrightarrow {SD} - \overrightarrow {BN} - \overrightarrow {CM} = \overrightarrow {SD} + \overrightarrow {DM} + \overrightarrow {MC} = \overrightarrow {SM} + \overrightarrow {MC} = \overrightarrow {SC} \)
Trả lời câu hỏi Vận dụng 2 trang 52SGK Toán 12 Kết nối tri thức
Thang cuốn tại các trung tâm thương mại, siêu thị hay nhà ga, sân bay thường có hai làn, trong đó một làn lên và một làn xuống. Khi thang cuốn chuyển động, vectơ biểu diễn vận tốc của mỗi làn có là hai vectơ đối nhau không? Giải thích vì sao.

Phương pháp giải:
Sử dụng kiến thức về hai vectơ đối nhau để giải thích: Trong không gian, vectơ có cùng độ dài và ngược hướng với vectơ \(\overrightarrow a \) được gọi là vectơ đối của vectơ \(\overrightarrow a \), kí hiệu là \( - \overrightarrow a \).
Lời giải chi tiết:
Vectơ biểu diễn vận tốc của mỗi làn có cùng độ lớn và hướng ngược nhau nên chúng là hai vectơ đối nhau.
Mục 2 của chương trình Toán 12 tập 1 - Kết nối tri thức tập trung vào việc nghiên cứu về giới hạn của hàm số. Đây là một khái niệm nền tảng quan trọng, đóng vai trò then chốt trong việc hiểu và giải quyết các bài toán về đạo hàm, tích phân và các ứng dụng của chúng trong các lĩnh vực khác.
Để hiểu rõ về giới hạn của hàm số tại một điểm, chúng ta cần nắm vững các khái niệm cơ bản như:
Việc tính giới hạn của hàm số có thể được thực hiện bằng nhiều phương pháp khác nhau, tùy thuộc vào dạng của hàm số. Một số phương pháp phổ biến bao gồm:
Khi x tiến tới vô cực (dương hoặc âm), giới hạn của hàm số có thể là một số thực, vô cực hoặc không tồn tại. Để tính giới hạn của hàm số tại vô cực, chúng ta thường sử dụng các phương pháp sau:
Bài 1: Tính limx→2 (x2 - 4) / (x - 2)
Lời giải:
limx→2 (x2 - 4) / (x - 2) = limx→2 (x - 2)(x + 2) / (x - 2) = limx→2 (x + 2) = 4
Bài 2: Tính limx→∞ (2x + 1) / (x - 3)
Lời giải:
limx→∞ (2x + 1) / (x - 3) = limx→∞ (2 + 1/x) / (1 - 3/x) = 2/1 = 2
Bài 3: Tính limx→0 sin(x) / x
Lời giải:
limx→0 sin(x) / x = 1 (Đây là một giới hạn lượng giác cơ bản)
Giới hạn là một khái niệm quan trọng trong toán học, có nhiều ứng dụng trong các lĩnh vực khác nhau, bao gồm:
Hy vọng rằng với những kiến thức và phương pháp giải bài tập được trình bày trong bài viết này, các em sẽ tự tin hơn trong việc học tập và giải quyết các bài toán về giới hạn của hàm số. Chúc các em học tốt!