Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 của giaitoan.edu.vn. Chúng tôi xin giới thiệu lời giải chi tiết và dễ hiểu cho mục 1 trang 26, 27 sách giáo khoa Toán 12 tập 1 chương trình Kết nối tri thức.
Với đội ngũ giáo viên giàu kinh nghiệm, chúng tôi cam kết cung cấp những lời giải chính xác, khoa học, giúp các em nắm vững kiến thức và tự tin giải quyết các bài tập tương tự.
Sơ đồ khảo sát hàm số
Đề bài
Trả lời câu hỏi Hoạt động 1 trang 26 SGK Toán 12 Kết nối tri thức
Cho hàm số \(y = {x^2} - 4x + 3\). Thực hiện lần lượt các yêu cầu sau:
a) Tính y’ và tìm các điểm tại đó \(y' = 0\).
b) Xét dấu y’ để tìm các khoảng đồng biến, khoảng nghịch biến và cực trị của hàm số.
c) Tính \(\mathop {\lim }\limits_{x \to - \infty } y\), \(\mathop {\lim }\limits_{x \to + \infty } y\) và lập bảng biến thiên của hàm số.
d) Vẽ đồ thị của hàm số và nhận xét về tính đối xứng của đồ thị.
Phương pháp giải - Xem chi tiết
a) Tính y’. Giải phương trình \(y' = 0\).
b) Sử dụng kiến thức về định lí về tính đồng biến, nghịch biến của hàm số để tìm khoảng đồng biến, nghịch biến: Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên khoảng K.
+ Nếu \(f'\left( x \right) > 0\) với mọi \(x \in K\) thì hàm số \(f\left( x \right)\) đồng biến trên khoảng K.
+ Nếu \(f'\left( x \right) < 0\) với mọi \(x \in K\) thì hàm số \(f\left( x \right)\) nghịch biến trên khoảng K.
Sử dụng kiến thức về định lí cực trị hàm số để tìm cực trị hàm số: Giả sử hàm số \(y = f\left( x \right)\) liên tục trên khoảng (a; b) chứa điểm \({x_0}\) và có đạo hàm trên các khoảng \(\left( {a;{x_0}} \right)\) và \(\left( {{x_0};b} \right)\). Khi đó:
+ Nếu \(f'\left( x \right) < 0\) với mọi \(x \in \left( {a;{x_0}} \right)\) và \(f'\left( x \right) > 0\) với mọi \(x \in \left( {{x_0};b} \right)\) thì điểm \({x_0}\) là một điểm cực tiểu của hàm số f(x).
+ Nếu \(f'\left( x \right) > 0\) với mọi \(x \in \left( {a;{x_0}} \right)\) và \(f'\left( x \right) < 0\) với mọi \(x \in \left( {{x_0};b} \right)\) thì điểm \({x_0}\) là một điểm cực đại của hàm số f(x).
d) Đồ thị hàm số bậc hai \(y = a{x^2} + bx + c\left( {a \ne 0} \right)\) nhận đường thẳng \(x = \frac{{ - b}}{{2a}}\) làm trục đối xứng.
Lời giải chi tiết
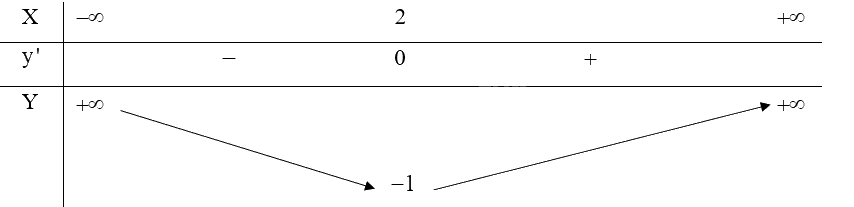
a) Tập xác định: \(D = \mathbb{R}\)
Ta có: \(y' = 2x - 4,y' = 0 \Leftrightarrow 2x - 4 = 0 \Leftrightarrow x = 2\)
Vậy với \(x = 2\) thì \(y' = 0\).
b) Trên khoảng \(\left( { - \infty ;2} \right)\), \(y' < 0\) nên hàm số nghịch biến. Trên khoảng \(\left( {2; + \infty } \right)\), \(y' > 0\) nên hàm số đồng biến.
Hàm số đạt cực tiểu tại \(x = 2,\) giá trị cực tiểu \({y_{CT}} = - 1\). Hàm số không có cực đại.
c) \(\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \left( {{x^2} - 4x + 3} \right) = \mathop {\lim }\limits_{x \to - \infty } \left[ {{x^2}\left( {1 - \frac{4}{x} + \frac{3}{{{x^2}}}} \right)} \right] = + \infty \)
\(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \left( {{x^2} - 4x + 3} \right) = \mathop {\lim }\limits_{x \to + \infty } \left[ {{x^2}\left( {1 - \frac{4}{x} + \frac{3}{{{x^2}}}} \right)} \right] = + \infty \)
Bảng biến thiên:
d) Đồ thị:
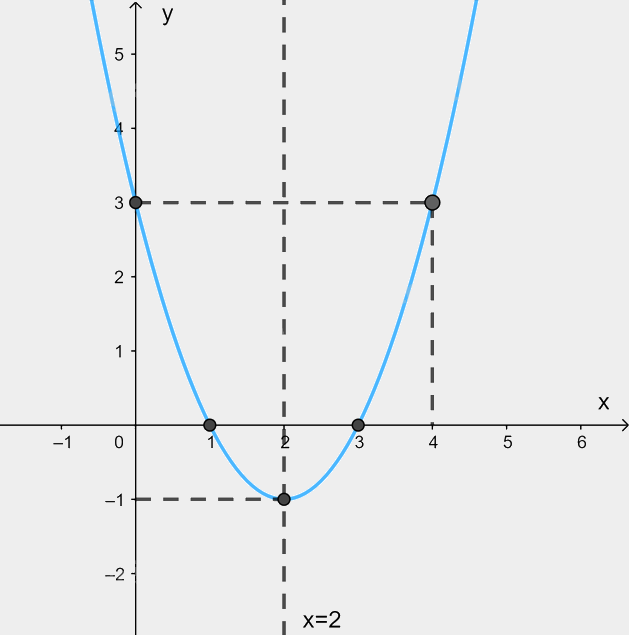
Giao điểm của đồ thị hàm số \(y = {x^2} - 4x + 3\) với trục tung là \(\left( {0;3} \right)\).
Ta có: \({x^2} - 4x + 3 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = 1\end{array} \right.\). Do đó, giao điểm của đồ thị hàm số với trục hoành là các điểm \(\left( {3;0} \right);\left( {1;0} \right)\).
Điểm \(\left( {4;3} \right)\) thuộc đồ thị hàm số \(y = {x^2} - 4x + 3\).
Đồ thị hàm số nhận đường thẳng \(x = 2\) làm trục đối xứng.
d) Đồ thị:
Giao điểm của đồ thị hàm số \(y = {x^2} - 4x + 3\) với trục tung là \(\left( {0;3} \right)\).
Ta có: \({x^2} - 4x + 3 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = 1\end{array} \right.\). Do đó, giao điểm của đồ thị hàm số với trục hoành là các điểm \(\left( {3;0} \right);\left( {1;0} \right)\).
Điểm \(\left( {4;3} \right)\) thuộc đồ thị hàm số \(y = {x^2} - 4x + 3\).
Đồ thị hàm số nhận đường thẳng \(x = 2\) làm trục đối xứng.
Mục 1 trang 26, 27 SGK Toán 12 tập 1 - Kết nối tri thức tập trung vào việc ôn tập và hệ thống hóa kiến thức về giới hạn của hàm số. Đây là nền tảng quan trọng để học sinh tiếp cận các khái niệm và kỹ năng phức tạp hơn trong chương trình Toán 12. Việc nắm vững kiến thức này không chỉ giúp học sinh giải quyết các bài tập trong sách giáo khoa mà còn là bước chuẩn bị tốt cho kỳ thi tốt nghiệp THPT và các kỳ thi khác.
Bài tập này yêu cầu học sinh vận dụng định nghĩa và các tính chất của giới hạn để tính toán giá trị của các giới hạn cho trước. Cần chú ý đến việc phân tích biểu thức, rút gọn và sử dụng các công thức giới hạn đặc biệt.
Ví dụ: Tính lim (x→2) (x2 - 4) / (x - 2). Ta có thể phân tích tử số thành (x - 2)(x + 2) và rút gọn biểu thức thành lim (x→2) (x + 2) = 4.
Bài tập này yêu cầu học sinh xác định giới hạn của hàm số khi x tiến tới vô cùng hoặc trừ vô cùng. Cần chú ý đến bậc cao nhất của tử số và mẫu số để xác định giới hạn.
Ví dụ: Tính lim (x→∞) (2x2 + 3x - 1) / (x2 + 5). Ta chia cả tử số và mẫu số cho x2, ta được lim (x→∞) (2 + 3/x - 1/x2) / (1 + 5/x2) = 2.
Bài tập này yêu cầu học sinh kiểm tra xem hàm số có liên tục tại một điểm hay không. Cần kiểm tra xem giới hạn của hàm số tại điểm đó có tồn tại và bằng với giá trị của hàm số tại điểm đó hay không.
Hy vọng với lời giải chi tiết và những hướng dẫn trên, các em học sinh đã nắm vững kiến thức và kỹ năng giải bài tập trong Mục 1 trang 26, 27 SGK Toán 12 tập 1 - Kết nối tri thức. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!