Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 tại giaitoan.edu.vn. Chúng tôi xin giới thiệu lời giải chi tiết và dễ hiểu cho mục 3 trang 8, 9, 10 sách giáo khoa Toán 12 tập 2 chương trình Kết nối tri thức.
Với đội ngũ giáo viên giàu kinh nghiệm, chúng tôi cam kết cung cấp những lời giải chính xác, đầy đủ, giúp các em nắm vững kiến thức và tự tin giải quyết các bài tập tương tự.
Nguyên hàm của một số hàm số thường gặp
Trả lời câu hỏi ? trang 8 SGK Toán 12 Kết nối tri thức
Bằng cách viết lại các hàm số sau dưới dạng lũy thừa \(y = {x^\alpha }\left( {x > 0} \right)\), hãy tính đạo hàm của các hàm số sau với \(x > 0\): \(y = \frac{1}{{{x^4}}},y = {x^{\sqrt 2 }},y = \frac{1}{{\sqrt[3]{x}}}\).
Phương pháp giải:
Sử dụng kiến thức về đạo hàm của hàm số lũy thừa để tính các đạo hàm: Hàm số lũy thừa \(y = {x^\alpha }\left( {\alpha \in \mathbb{R}} \right)\) có đạo hàm với mọi \(x > 0\) và \(\left( {{x^\alpha }} \right)' = \alpha .{x^{\alpha - 1}}\)
Lời giải chi tiết:
Ta có: \(y = \frac{1}{{{x^4}}} = {x^{ - 4}}\) nên \(y' = - 4{x^{ - 5}}\); \(y = {x^{\sqrt 2 }} = {x^{\frac{1}{2}}}\) nên \(y' = \frac{1}{2}{x^{ - \frac{1}{2}}} = \frac{1}{{2\sqrt x }}\), \(y = \frac{1}{{\sqrt[3]{x}}} = {x^{\frac{{ - 1}}{3}}}\) nên \(y' = \frac{{ - 1}}{3}{x^{\frac{{ - 4}}{3}}} = \frac{{ - 1}}{{3{x^{\frac{4}{3}}}}}\).
Trả lời câu hỏi Hoạt động 5 trang 8 SGK Toán 12 Kết nối tri thức
a) Với \(\alpha \ne - 1\), tính đạo hàm của hàm số \(y = \frac{{{x^{\alpha + 1}}}}{{\alpha + 1}}\left( {x > 0} \right)\).
b) Cho hàm số \(y = \ln \left| x \right|\left( {x \ne 0} \right)\). Tính đạo hàm của hàm số này trong hai trường hợp: \(x > 0\) và \(x < 0\).
Phương pháp giải:
Sử dụng kiến thức về khái niệm nguyên hàm của một hàm số để tính: Cho hàm số f(x) xác định trên một khoảng K (hoặc một đoạn, hoặc một nửa khoảng). Hàm số F(x) được gọi là một nguyên hàm của hàm số f(x) trên K nếu \(F'\left( x \right) = f\left( x \right)\) với mọi x thuộc K.
Sử dụng kiến thức về họ nguyên hàm của một hàm số để tính: Để tìm nguyên hàm của hàm số f(x) trên K, ta chỉ cần tìm một nguyên hàm F(x) của f(x) trên K và khi đó \(\int {f\left( x \right)dx = F\left( x \right) + C} \), C là hằng số.
Sử dụng kiến thức về đạo hàm của hàm số lũy thừa để tính các đạo hàm: Hàm số lũy thừa \(y = {x^\alpha }\left( {\alpha \in \mathbb{R}} \right)\) có đạo hàm với mọi \(x > 0\) và \(\left( {{x^\alpha }} \right)' = \alpha .{x^{\alpha - 1}}\)
Lời giải chi tiết:
a) Vì \(y' = {\left( {\frac{{{x^{\alpha + 1}}}}{{\alpha + 1}}} \right)'} = \frac{{\left( {\alpha + 1} \right){x^\alpha }}}{{\alpha + 1}} = {x^\alpha }\) với mọi \(x > 0\), \(\alpha \ne - 1\).
b) Ta có: \(y' = \left( {\ln \left| x \right|} \right)' = \frac{1}{{\left| x \right|}}\).
Với \(x > 0\) thì \(y' = \frac{1}{x}\).
Với \(x < 0\) thì \(y' = \frac{1}{{ - x}}\).
Trả lời câu hỏi Luyện tập 5 trang 9 SGK Toán 12 Kết nối tri thức
Tìm:
a) \(\int {\frac{1}{{{x^4}}}dx} \);
b) \(\int {x\sqrt x dx\left( {x > 0} \right)} \);
c) \(\int {\left( {\frac{3}{x} - 5\sqrt[3]{x}} \right)dx\left( {x > 0} \right)} \).
Phương pháp giải:
Sử dụng kiến thức về tính chất cơ bản của nguyên hàm để tính: \(\int {kf\left( x \right)dx} = k\int {f\left( x \right)dx} \)
Sử dụng kiến thức về nguyên hàm một tổng để tính: \(\int {\left[ {f\left( x \right) - g\left( x \right)} \right]} \,dx = \int {f\left( x \right)dx - \int {g\left( x \right)dx} } \)
Sử dụng kiến thức về nguyên hàm của hàm số lũy thừa để tính:
\(\int {{x^\alpha }dx} = \frac{{{x^{\alpha + 1}}}}{{\alpha + 1}} + C\left( {\alpha \ne - 1} \right)\)
Lời giải chi tiết:
a) \(\int {\frac{1}{{{x^4}}}dx} = \int {{x^{ - 4}}dx} = \frac{{{x^{ - 4 + 1}}}}{{ - 4 + 1}} + C = \frac{{{x^{ - 3}}}}{{ - 3}} + C = \frac{{ - 1}}{{3{x^3}}} + C\);
b) \(\int {x\sqrt x dx = } \int {{x^{\frac{3}{2}}}dx = } \frac{{{x^{\frac{3}{2} + 1}}}}{{\frac{3}{2} + 1}} + C = \frac{2}{5}{x^2}\sqrt x + C\);
c) \(\int {\left( {\frac{3}{x} - 5\sqrt[3]{x}} \right)dx = \int {\frac{3}{x}dx - \int {5\sqrt[3]{x}} dx = 3\int {\frac{1}{x}dx - 5\int {{x^{\frac{1}{3}}}} dx = 3\ln \left| x \right| - 5.\frac{{{x^{\frac{4}{3}}}}}{{\frac{4}{3}}} + C} } } \)
\( = 3\ln \left| x \right| - \frac{{15x\sqrt[3]{x}}}{4} + C\).
Trả lời câu hỏi Luyện tập 6 trang 9 SGK Toán 12 Kết nối tri thức
Tìm:
a) \(\int {\left( {3\cos x - 4\sin x} \right)dx} \);
b) \(\int {\left( {\frac{1}{{{{\cos }^2}x}} - \frac{1}{{{{\sin }^2}x}}} \right)dx} \).
Phương pháp giải:
Sử dụng kiến thức về tính chất cơ bản của nguyên hàm để tính: \(\int {kf\left( x \right)dx} = k\int {f\left( x \right)dx} \)
Sử dụng kiến thức về nguyên hàm một tổng để tính: \(\int {\left[ {f\left( x \right) - g\left( x \right)} \right]} \,dx = \int {f\left( x \right)dx - \int {g\left( x \right)dx} } \)
Sử dụng kiến thức về nguyên hàm của hàm số lượng giác để tính:
\(\int {\cos x} dx = \sin x + C,\int {\sin x} dx = - \cos x + C,\int {\frac{1}{{{{\cos }^2}x}}} dx = \tan x + C,\int {\frac{1}{{{{\sin }^2}x}}} dx = - \cot x + C\)
Lời giải chi tiết:
a) \(\int {\left( {3\cos x - 4\sin x} \right)dx} = 3\int {\cos x} dx - 4\int {\sin x} dx = 3\sin x + 4\cos x + C\);
b) \(\int {\left( {\frac{1}{{{{\cos }^2}x}} - \frac{1}{{{{\sin }^2}x}}} \right)dx} = \int {\frac{1}{{{{\cos }^2}x}}} dx - \int {\frac{1}{{{{\sin }^2}x}}} dx = \tan x + \cot x + C\).
Trả lời câu hỏi Luyện tập 7 trang 10 SGK Toán 12 Kết nối tri thức
Tìm:
a) \(\int {{4^x}dx} \);
b) \(\int {\frac{1}{{{e^x}}}dx} \);
c) \(\int {\left( {{{2.3}^x} - \frac{1}{3}{{.7}^x}} \right)dx} \).
Phương pháp giải:
Sử dụng kiến thức về tính chất cơ bản của nguyên hàm để tính: \(\int {kf\left( x \right)dx} = k\int {f\left( x \right)dx} \)
Sử dụng kiến thức về nguyên hàm một tổng để tính: \(\int {\left[ {f\left( x \right) - g\left( x \right)} \right]} \,dx = \int {f\left( x \right)dx - \int {g\left( x \right)dx} } \)
Sử dụng kiến thức về nguyên hàm của hàm số mũ để tính:
\(\int {{e^x}dx} = {e^x} + C,\int {{a^x}dx} = \frac{{{a^x}}}{{\ln a}} + C\left( {0 < a \ne 1} \right)\)
Lời giải chi tiết:
a) \(\int {{4^x}dx} = \frac{{{4^x}}}{{\ln 4}} + C\);
b) \(\int {\frac{1}{{{e^x}}}dx} = \int {{{\left( {\frac{1}{e}} \right)}^x}dx} = \frac{{{{\left( {\frac{1}{e}} \right)}^x}}}{{\ln \frac{1}{e}}} + C = - {e^{ - x}} + C\);
c) \(\int {\left( {{{2.3}^x} - \frac{1}{3}{{.7}^x}} \right)dx} = 2\int {{3^x}} dx - \frac{1}{3}\int {{7^x}} dx = \frac{{{{2.3}^x}}}{{\ln 3}} - \frac{{{7^x}}}{{3\ln 7}} + C\).
Trả lời câu hỏi Hoạt động 6 trang 9 SGK Toán 12 Kết nối tri thức
a) Tính đạo hàm của các hàm số sau và nêu kết quả tương ứng vào bảng dưới đây.

b) Sử dụng kết quả ở câu a, tìm nguyên hàm của các hàm số cho trong bảng dưới đây.
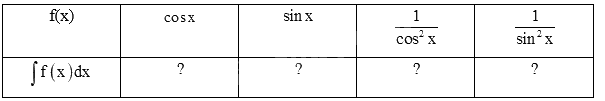
Phương pháp giải:
a) Sử dụng kiến thức về đạo hàm của hàm số lượng giác để tính:
\(\left( {\sin x} \right)' = \cos x,\left( {\cos x} \right)' = - \sin x,\left( {\tan x} \right)' = \frac{1}{{{{\cos }^2}x}},\left( {\cot x} \right)' = \frac{{ - 1}}{{{{\sin }^2}x}}\)
b) Sử dụng kiến thức về khái niệm nguyên hàm của một hàm số để tính: Cho hàm số f(x) xác định trên một khoảng K (hoặc một đoạn, hoặc một nửa khoảng). Hàm số F(x) được gọi là một nguyên hàm của hàm số f(x) trên K nếu \(F'\left( x \right) = f\left( x \right)\) với mọi x thuộc K.
Sử dụng kiến thức về họ nguyên hàm của một hàm số để tính: Để tìm nguyên hàm của hàm số f(x) trên K, ta chỉ cần tìm một nguyên hàm F(x) của f(x) trên K và khi đó \(\int {f\left( x \right)dx = F\left( x \right) + C} \), C là hằng số.
Lời giải chi tiết:
a)

b)
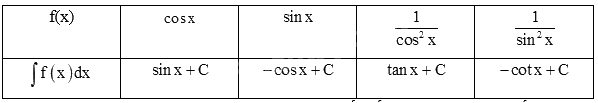
Trả lời câu hỏi Hoạt động 7 trang 10 SGK Toán 12 Kết nối tri thức
a) Tính đạo hàm của các hàm số sau và nêu kết quả tương ứng vào bảng dưới đây.
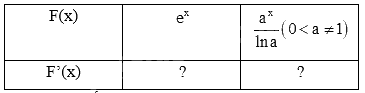
b) Sử dụng kết quả ở câu a, tìm nguyên hàm của các hàm số cho trong bảng dưới đây.
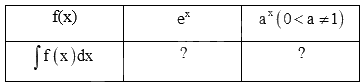
Phương pháp giải:
a) Sử dụng kiến thức về đạo hàm của hàm số mũ để tính: \(\left( {{e^x}} \right)' = {e^x},\left( {{a^x}} \right)' = {a^x}.\ln a\)
b) Sử dụng kiến thức về khái niệm nguyên hàm của một hàm số để tính: Cho hàm số f(x) xác định trên một khoảng K (hoặc một đoạn, hoặc một nửa khoảng). Hàm số F(x) được gọi là một nguyên hàm của hàm số f(x) trên K nếu \(F'\left( x \right) = f\left( x \right)\) với mọi x thuộc K.
Sử dụng kiến thức về họ nguyên hàm của một hàm số để tính: Để tìm nguyên hàm của hàm số f(x) trên K, ta chỉ cần tìm một nguyên hàm F(x) của f(x) trên K và khi đó \(\int {f\left( x \right)dx = F\left( x \right) + C} \), C là hằng số.
Lời giải chi tiết:
a)
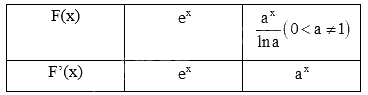
b)

Trả lời câu hỏi ? trang 8 SGK Toán 12 Kết nối tri thức
Bằng cách viết lại các hàm số sau dưới dạng lũy thừa \(y = {x^\alpha }\left( {x > 0} \right)\), hãy tính đạo hàm của các hàm số sau với \(x > 0\): \(y = \frac{1}{{{x^4}}},y = {x^{\sqrt 2 }},y = \frac{1}{{\sqrt[3]{x}}}\).
Phương pháp giải:
Sử dụng kiến thức về đạo hàm của hàm số lũy thừa để tính các đạo hàm: Hàm số lũy thừa \(y = {x^\alpha }\left( {\alpha \in \mathbb{R}} \right)\) có đạo hàm với mọi \(x > 0\) và \(\left( {{x^\alpha }} \right)' = \alpha .{x^{\alpha - 1}}\)
Lời giải chi tiết:
Ta có: \(y = \frac{1}{{{x^4}}} = {x^{ - 4}}\) nên \(y' = - 4{x^{ - 5}}\); \(y = {x^{\sqrt 2 }} = {x^{\frac{1}{2}}}\) nên \(y' = \frac{1}{2}{x^{ - \frac{1}{2}}} = \frac{1}{{2\sqrt x }}\), \(y = \frac{1}{{\sqrt[3]{x}}} = {x^{\frac{{ - 1}}{3}}}\) nên \(y' = \frac{{ - 1}}{3}{x^{\frac{{ - 4}}{3}}} = \frac{{ - 1}}{{3{x^{\frac{4}{3}}}}}\).
Trả lời câu hỏi Hoạt động 5 trang 8 SGK Toán 12 Kết nối tri thức
a) Với \(\alpha \ne - 1\), tính đạo hàm của hàm số \(y = \frac{{{x^{\alpha + 1}}}}{{\alpha + 1}}\left( {x > 0} \right)\).
b) Cho hàm số \(y = \ln \left| x \right|\left( {x \ne 0} \right)\). Tính đạo hàm của hàm số này trong hai trường hợp: \(x > 0\) và \(x < 0\).
Phương pháp giải:
Sử dụng kiến thức về khái niệm nguyên hàm của một hàm số để tính: Cho hàm số f(x) xác định trên một khoảng K (hoặc một đoạn, hoặc một nửa khoảng). Hàm số F(x) được gọi là một nguyên hàm của hàm số f(x) trên K nếu \(F'\left( x \right) = f\left( x \right)\) với mọi x thuộc K.
Sử dụng kiến thức về họ nguyên hàm của một hàm số để tính: Để tìm nguyên hàm của hàm số f(x) trên K, ta chỉ cần tìm một nguyên hàm F(x) của f(x) trên K và khi đó \(\int {f\left( x \right)dx = F\left( x \right) + C} \), C là hằng số.
Sử dụng kiến thức về đạo hàm của hàm số lũy thừa để tính các đạo hàm: Hàm số lũy thừa \(y = {x^\alpha }\left( {\alpha \in \mathbb{R}} \right)\) có đạo hàm với mọi \(x > 0\) và \(\left( {{x^\alpha }} \right)' = \alpha .{x^{\alpha - 1}}\)
Lời giải chi tiết:
a) Vì \(y' = {\left( {\frac{{{x^{\alpha + 1}}}}{{\alpha + 1}}} \right)'} = \frac{{\left( {\alpha + 1} \right){x^\alpha }}}{{\alpha + 1}} = {x^\alpha }\) với mọi \(x > 0\), \(\alpha \ne - 1\).
b) Ta có: \(y' = \left( {\ln \left| x \right|} \right)' = \frac{1}{{\left| x \right|}}\).
Với \(x > 0\) thì \(y' = \frac{1}{x}\).
Với \(x < 0\) thì \(y' = \frac{1}{{ - x}}\).
Trả lời câu hỏi Luyện tập 5 trang 9 SGK Toán 12 Kết nối tri thức
Tìm:
a) \(\int {\frac{1}{{{x^4}}}dx} \);
b) \(\int {x\sqrt x dx\left( {x > 0} \right)} \);
c) \(\int {\left( {\frac{3}{x} - 5\sqrt[3]{x}} \right)dx\left( {x > 0} \right)} \).
Phương pháp giải:
Sử dụng kiến thức về tính chất cơ bản của nguyên hàm để tính: \(\int {kf\left( x \right)dx} = k\int {f\left( x \right)dx} \)
Sử dụng kiến thức về nguyên hàm một tổng để tính: \(\int {\left[ {f\left( x \right) - g\left( x \right)} \right]} \,dx = \int {f\left( x \right)dx - \int {g\left( x \right)dx} } \)
Sử dụng kiến thức về nguyên hàm của hàm số lũy thừa để tính:
\(\int {{x^\alpha }dx} = \frac{{{x^{\alpha + 1}}}}{{\alpha + 1}} + C\left( {\alpha \ne - 1} \right)\)
Lời giải chi tiết:
a) \(\int {\frac{1}{{{x^4}}}dx} = \int {{x^{ - 4}}dx} = \frac{{{x^{ - 4 + 1}}}}{{ - 4 + 1}} + C = \frac{{{x^{ - 3}}}}{{ - 3}} + C = \frac{{ - 1}}{{3{x^3}}} + C\);
b) \(\int {x\sqrt x dx = } \int {{x^{\frac{3}{2}}}dx = } \frac{{{x^{\frac{3}{2} + 1}}}}{{\frac{3}{2} + 1}} + C = \frac{2}{5}{x^2}\sqrt x + C\);
c) \(\int {\left( {\frac{3}{x} - 5\sqrt[3]{x}} \right)dx = \int {\frac{3}{x}dx - \int {5\sqrt[3]{x}} dx = 3\int {\frac{1}{x}dx - 5\int {{x^{\frac{1}{3}}}} dx = 3\ln \left| x \right| - 5.\frac{{{x^{\frac{4}{3}}}}}{{\frac{4}{3}}} + C} } } \)
\( = 3\ln \left| x \right| - \frac{{15x\sqrt[3]{x}}}{4} + C\).
Trả lời câu hỏi Hoạt động 6 trang 9 SGK Toán 12 Kết nối tri thức
a) Tính đạo hàm của các hàm số sau và nêu kết quả tương ứng vào bảng dưới đây.

b) Sử dụng kết quả ở câu a, tìm nguyên hàm của các hàm số cho trong bảng dưới đây.
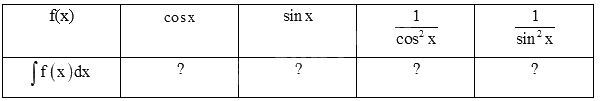
Phương pháp giải:
a) Sử dụng kiến thức về đạo hàm của hàm số lượng giác để tính:
\(\left( {\sin x} \right)' = \cos x,\left( {\cos x} \right)' = - \sin x,\left( {\tan x} \right)' = \frac{1}{{{{\cos }^2}x}},\left( {\cot x} \right)' = \frac{{ - 1}}{{{{\sin }^2}x}}\)
b) Sử dụng kiến thức về khái niệm nguyên hàm của một hàm số để tính: Cho hàm số f(x) xác định trên một khoảng K (hoặc một đoạn, hoặc một nửa khoảng). Hàm số F(x) được gọi là một nguyên hàm của hàm số f(x) trên K nếu \(F'\left( x \right) = f\left( x \right)\) với mọi x thuộc K.
Sử dụng kiến thức về họ nguyên hàm của một hàm số để tính: Để tìm nguyên hàm của hàm số f(x) trên K, ta chỉ cần tìm một nguyên hàm F(x) của f(x) trên K và khi đó \(\int {f\left( x \right)dx = F\left( x \right) + C} \), C là hằng số.
Lời giải chi tiết:
a)

b)
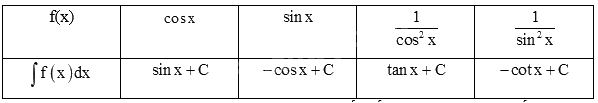
Trả lời câu hỏi Luyện tập 6 trang 9 SGK Toán 12 Kết nối tri thức
Tìm:
a) \(\int {\left( {3\cos x - 4\sin x} \right)dx} \);
b) \(\int {\left( {\frac{1}{{{{\cos }^2}x}} - \frac{1}{{{{\sin }^2}x}}} \right)dx} \).
Phương pháp giải:
Sử dụng kiến thức về tính chất cơ bản của nguyên hàm để tính: \(\int {kf\left( x \right)dx} = k\int {f\left( x \right)dx} \)
Sử dụng kiến thức về nguyên hàm một tổng để tính: \(\int {\left[ {f\left( x \right) - g\left( x \right)} \right]} \,dx = \int {f\left( x \right)dx - \int {g\left( x \right)dx} } \)
Sử dụng kiến thức về nguyên hàm của hàm số lượng giác để tính:
\(\int {\cos x} dx = \sin x + C,\int {\sin x} dx = - \cos x + C,\int {\frac{1}{{{{\cos }^2}x}}} dx = \tan x + C,\int {\frac{1}{{{{\sin }^2}x}}} dx = - \cot x + C\)
Lời giải chi tiết:
a) \(\int {\left( {3\cos x - 4\sin x} \right)dx} = 3\int {\cos x} dx - 4\int {\sin x} dx = 3\sin x + 4\cos x + C\);
b) \(\int {\left( {\frac{1}{{{{\cos }^2}x}} - \frac{1}{{{{\sin }^2}x}}} \right)dx} = \int {\frac{1}{{{{\cos }^2}x}}} dx - \int {\frac{1}{{{{\sin }^2}x}}} dx = \tan x + \cot x + C\).
Trả lời câu hỏi Hoạt động 7 trang 10 SGK Toán 12 Kết nối tri thức
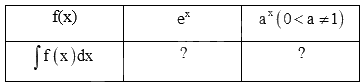
a) Tính đạo hàm của các hàm số sau và nêu kết quả tương ứng vào bảng dưới đây.
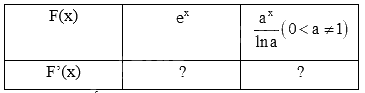
b) Sử dụng kết quả ở câu a, tìm nguyên hàm của các hàm số cho trong bảng dưới đây.
Phương pháp giải:
a) Sử dụng kiến thức về đạo hàm của hàm số mũ để tính: \(\left( {{e^x}} \right)' = {e^x},\left( {{a^x}} \right)' = {a^x}.\ln a\)
b) Sử dụng kiến thức về khái niệm nguyên hàm của một hàm số để tính: Cho hàm số f(x) xác định trên một khoảng K (hoặc một đoạn, hoặc một nửa khoảng). Hàm số F(x) được gọi là một nguyên hàm của hàm số f(x) trên K nếu \(F'\left( x \right) = f\left( x \right)\) với mọi x thuộc K.
Sử dụng kiến thức về họ nguyên hàm của một hàm số để tính: Để tìm nguyên hàm của hàm số f(x) trên K, ta chỉ cần tìm một nguyên hàm F(x) của f(x) trên K và khi đó \(\int {f\left( x \right)dx = F\left( x \right) + C} \), C là hằng số.
Lời giải chi tiết:
a)
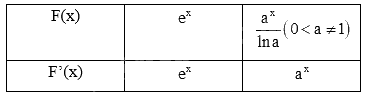
b)

Trả lời câu hỏi Luyện tập 7 trang 10 SGK Toán 12 Kết nối tri thức
Tìm:
a) \(\int {{4^x}dx} \);
b) \(\int {\frac{1}{{{e^x}}}dx} \);
c) \(\int {\left( {{{2.3}^x} - \frac{1}{3}{{.7}^x}} \right)dx} \).
Phương pháp giải:
Sử dụng kiến thức về tính chất cơ bản của nguyên hàm để tính: \(\int {kf\left( x \right)dx} = k\int {f\left( x \right)dx} \)
Sử dụng kiến thức về nguyên hàm một tổng để tính: \(\int {\left[ {f\left( x \right) - g\left( x \right)} \right]} \,dx = \int {f\left( x \right)dx - \int {g\left( x \right)dx} } \)
Sử dụng kiến thức về nguyên hàm của hàm số mũ để tính:
\(\int {{e^x}dx} = {e^x} + C,\int {{a^x}dx} = \frac{{{a^x}}}{{\ln a}} + C\left( {0 < a \ne 1} \right)\)
Lời giải chi tiết:
a) \(\int {{4^x}dx} = \frac{{{4^x}}}{{\ln 4}} + C\);
b) \(\int {\frac{1}{{{e^x}}}dx} = \int {{{\left( {\frac{1}{e}} \right)}^x}dx} = \frac{{{{\left( {\frac{1}{e}} \right)}^x}}}{{\ln \frac{1}{e}}} + C = - {e^{ - x}} + C\);
c) \(\int {\left( {{{2.3}^x} - \frac{1}{3}{{.7}^x}} \right)dx} = 2\int {{3^x}} dx - \frac{1}{3}\int {{7^x}} dx = \frac{{{{2.3}^x}}}{{\ln 3}} - \frac{{{7^x}}}{{3\ln 7}} + C\).
Mục 3 trong SGK Toán 12 tập 2 Kết nối tri thức thường tập trung vào một chủ đề cụ thể trong chương trình học. Để giải quyết hiệu quả các bài tập trong mục này, học sinh cần nắm vững kiến thức lý thuyết liên quan, hiểu rõ các định nghĩa, định lý và công thức quan trọng. Bài viết này sẽ cung cấp lời giải chi tiết cho từng bài tập trang 8, 9, 10, đồng thời phân tích các phương pháp giải và những điểm cần lưu ý.
Chúng ta sẽ bắt đầu với việc giải chi tiết các bài tập từ 1 đến hết trang 8. Mỗi bài tập sẽ được trình bày đầy đủ các bước giải, kèm theo giải thích rõ ràng để học sinh dễ dàng theo dõi và hiểu được logic của bài toán. Ví dụ, nếu bài tập yêu cầu tính đạo hàm của một hàm số, chúng ta sẽ áp dụng các quy tắc đạo hàm cơ bản và các công thức đạo hàm đặc biệt để tìm ra kết quả chính xác.
Tiếp theo, chúng ta sẽ chuyển sang giải các bài tập trên trang 9. Các bài tập ở trang này có thể liên quan đến việc ứng dụng đạo hàm để giải quyết các bài toán thực tế, chẳng hạn như tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số, hoặc xét tính đơn điệu của hàm số. Chúng ta sẽ sử dụng các phương pháp tối ưu hóa để tìm ra lời giải hiệu quả nhất.
Cuối cùng, chúng ta sẽ giải các bài tập còn lại trên trang 10. Các bài tập ở trang này có thể là các bài tập tổng hợp, yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các bài toán phức tạp hơn. Chúng ta sẽ phân tích kỹ lưỡng từng bài toán và đưa ra lời giải chi tiết, rõ ràng.
Bài tập: Tính đạo hàm của hàm số y = x3 + 2x2 - 5x + 1.
Lời giải:
y' = 3x2 + 4x - 5
Hy vọng rằng với lời giải chi tiết và những hướng dẫn cụ thể trong bài viết này, các em học sinh sẽ tự tin hơn khi giải các bài tập mục 3 trang 8,9,10 SGK Toán 12 tập 2 Kết nối tri thức. Hãy luyện tập thường xuyên để củng cố kiến thức và nâng cao kỹ năng giải toán của mình. Chúc các em học tập tốt!