Chào mừng bạn đến với bài học về lý thuyết biểu thức tọa độ của các phép toán vecto trong chương trình Toán 12 Kết nối tri thức.
Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng về cách biểu diễn các phép toán vecto bằng tọa độ, giúp bạn giải quyết các bài toán một cách hiệu quả và chính xác.
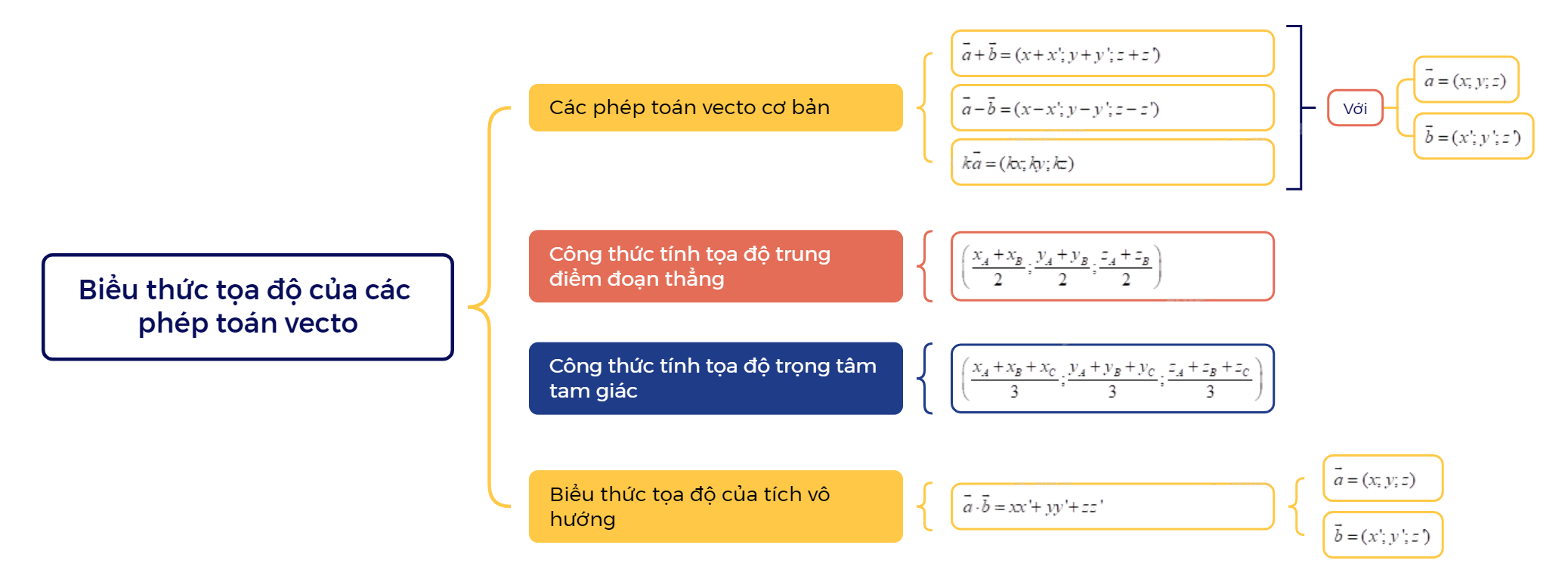
1. Biểu thức tọa độ của phép cộng hai vecto, phép trừ hai vecto, phép nhân một số với một vecto
1. Biểu thức tọa độ của phép cộng hai vecto, phép trừ hai vecto, phép nhân một số với một vecto
Các phép toán vecto cơ bản
Trong không gian Oxyz, cho hai vecto \(\overrightarrow a = (x;y;z)\) và \(\overrightarrow b = (x';y';z')\). Ta có: \(\overrightarrow a + \overrightarrow b = (x + x';y + y';z + z')\) \(\overrightarrow a - \overrightarrow b = (x - x';y - y';z - z')\) \(k\overrightarrow a = (kx;ky;kz)\) với k là một số thực |
Công thức tính tọa độ trung điểm đoạn thẳng và trọng tâm tam giác
Trong không gian Oxyz, cho ba điểm không thẳng hàng \(A({x_A};{y_A};{z_A}),B({x_B};{y_B};{z_B}),C({x_C};{y_C};{z_C})\). Khi đó: Tọa độ trung điểm của đoạn thẳng AB là \[\left( {\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2};\frac{{{z_A} + {z_B}}}{2}} \right)\] Tọa độ trọng tâm tam giác ABC là \[\left( {\frac{{{x_A} + {x_B} + {x_C}}}{3};\frac{{{y_A} + {y_B} + {y_C}}}{3};\frac{{{z_A} + {z_B} + {z_C}}}{3}} \right)\] |
2. Biểu thức tọa độ của tích vô hướng
Trong không gian Oxyz, tích vô hướng của hai vecto \(\overrightarrow a = (x;y;z)\) và \(\overrightarrow b = (x';y';z')\) được xác định bởi công thức \(\overrightarrow a \cdot \overrightarrow b = xx' + yy' + zz'\) |
3. Vận dụng tọa độ của vecto trong một số bài toán có liên quan đến thực tiễn
Ví dụ: Trong không gian với một hệ trục cho trước (đơn vị đo km), ra đa phát hiện một chiếc máy bay di chuyển với vận tốc và hướng không đổi từ điểm A(800;500;7) đến điểm B (940;550;8) trong 10 phút. Nếu máy bay tiếp tục giữ nguyên vận tốc và hướng bay thì tọa độ của máy bay sau 5 phút tiếp theo là gì?
Giải:
Gọi C(x;y;z) là vị trí của máy bay sau 5 phút tiếp theo. Vì hướng của máy bay không đổi nên \(\overrightarrow {AB} \) và \(\overrightarrow {BC} \) cùng hướng. Do vận tốc bay không đổi và thời gian bay từ A đến B gấp đôi thời gian bay từ B đến C nên AB = 2BC.
Do đó, \(\overrightarrow {BC} = \frac{1}{2}\overrightarrow {AB} = \left( {\frac{{940 - 800}}{2};\frac{{550 - 500}}{2};\frac{{8 - 7}}{2}} \right) = \left( {70;25;0,5} \right)\).
Mặt khác, \(\overrightarrow {BC} = (x - 940;y - 550;z - 8)\) nên \(\left\{ \begin{array}{l}x - 940 = 70\\y - 550 = 25\\z - 8 = 0,5\end{array} \right.\).
Từ đó \(\left\{ \begin{array}{l}x = 1010\\y = 575\\z = 8,5\end{array} \right.\) và vì vậy C(1010;575;8,5).
Vậy tọa độ của máy bay sau 5 phút tiếp theo là (1010;575;8,5).
Trong chương trình Toán 12 Kết nối tri thức, phần hình học vecto đóng vai trò quan trọng, đặc biệt là việc ứng dụng biểu thức tọa độ để giải quyết các bài toán. Bài viết này sẽ trình bày chi tiết lý thuyết về biểu thức tọa độ của các phép toán vecto, bao gồm cộng, trừ, nhân với một số, tích vô hướng và tích có hướng.
Vectơ là một đoạn thẳng có hướng. Trong mặt phẳng tọa độ, một vectơ được xác định bởi hai điểm đầu và cuối. Vectơ a = (x; y) có điểm đầu là A(xA; yA) và điểm cuối là B(xB; yB) thì x = xB - xA và y = yB - yA.
Tích vô hướng của hai vectơ a = (x1; y1) và b = (x2; y2) được ký hiệu là a.b và được tính bằng công thức: a.b = x1x2 + y1y2.
Tính chất của tích vô hướng:
Trong không gian Oxyz, cho hai vectơ a = (x1; y1; z1) và b = (x2; y2; z2). Tích có hướng của a và b, ký hiệu là [a, b], là một vectơ có:
Tích có hướng được tính bằng công thức:
[a, b] = (y1z2 - z1y2; z1x2 - x1z2; x1y2 - y1x2)
Biểu thức tọa độ giúp đơn giản hóa việc tính toán các phép toán vecto, đặc biệt trong các bài toán liên quan đến hình học giải tích. Ví dụ:
Ví dụ 1: Cho a = (2; -1) và b = (1; 3). Tính a + b và a - b.
Giải:
a + b = (2 + 1; -1 + 3) = (3; 2)
a - b = (2 - 1; -1 - 3) = (1; -4)
Ví dụ 2: Cho a = (1; 2; 3) và b = (-1; 0; 1). Tính tích vô hướng a.b.
Giải:
a.b = (1)(-1) + (2)(0) + (3)(1) = -1 + 0 + 3 = 2
Lý thuyết về biểu thức tọa độ của các phép toán vecto là nền tảng quan trọng để giải quyết các bài toán hình học trong chương trình Toán 12 Kết nối tri thức. Việc nắm vững các công thức và tính chất liên quan sẽ giúp bạn tự tin hơn trong quá trình học tập và làm bài.