Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 12. Chúng tôi giúp bạn nắm vững kiến thức và tự tin giải quyết các bài toán trong sách giáo khoa.
Mục 2 trang 51 SGK Toán 12 tập 2 - Kết nối tri thức là một phần quan trọng trong chương trình học. Bài viết này sẽ cung cấp đáp án, phương pháp giải và giải thích chi tiết để bạn hiểu rõ hơn về nội dung này.
CÔNG THỨC TÍNH GÓC GIỮA ĐƯỜNG THẲNG VÀ MẶT PHẲNG
Trả lời câu hỏi Luyện tập 2 trang 51 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, tính góc giữa đường thẳng \(\Delta \) và mặt phẳng (P), với:
\(\Delta :\frac{{x + 2}}{{ - 1}} = \frac{{y - 4}}{2} = \frac{{z + 1}}{1},\left( P \right):x - y + z - 1 = 0\).
Phương pháp giải:
Sử dụng kiến thức về góc giữa đường thẳng và mặt phẳng để tính: Trong không gian Oxyz, cho đường thẳng \(\Delta \) có vectơ chỉ phương \(\overrightarrow u = \left( {a;b;c} \right)\) và mặt phẳng (P) có vectơ pháp tuyến \(\overrightarrow n = \left( {A;B;C} \right)\).
Khi đó: \(\sin \left( {\Delta ,\left( P \right)} \right) = \left| {\cos \left( {\overrightarrow u ,\overrightarrow n } \right)} \right| = \frac{{\left| {aA + bB + cC} \right|}}{{\sqrt {{a^2} + {b^2} + {c^2}} .\sqrt {{A^2} + {B^2} + {C^2}} }}\)
Lời giải chi tiết:
Đường thẳng \(\Delta \) có vectơ chỉ phương \(\overrightarrow u = \left( { - 1;2;1} \right)\), mặt phẳng (P) có vectơ pháp tuyến \(\overrightarrow n = \left( {1; - 1;1} \right)\). Ta có: \(\sin \left( {\Delta ,\left( P \right)} \right) = \frac{{\left| {\left( { - 1} \right).1 + 2.\left( { - 1} \right) + 1.1} \right|}}{{\sqrt {{{\left( { - 1} \right)}^2} + {2^2} + {1^2}} .\sqrt {{1^2} + {{\left( { - 1} \right)}^2} + {1^2}} }} = \frac{{\sqrt 2 }}{3}\)
Do đó, góc giữa đường thẳng \(\Delta \) và mặt phẳng (P) khoảng \(28,{1^0}\).
Trả lời câu hỏi Hoạt động 2 trang 51 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, cho đường thẳng \(\Delta \) và mặt phẳng (P). Xét \(\overrightarrow u = \left( {a;b;c} \right)\) là một vectơ chỉ phương của \(\Delta \) và \(\overrightarrow n = \left( {A;B;C} \right)\) (với giá \(\Delta '\)) là một vectơ pháp tuyến của (P). (H.5.35)
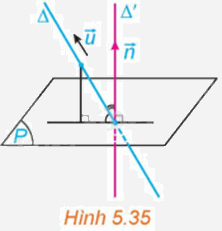
a) Hãy tìm mối quan hệ giữa các góc \(\left( {\Delta ,\left( P \right)} \right)\) và \(\left( {\Delta ,\Delta '} \right)\).
b) Có nhận xét gì về mối quan hệ giữa \(\sin \left( {\Delta ,\Delta '} \right)\) và \(\left| {\cos \left( {\overrightarrow u ,\overrightarrow n } \right)} \right|\)?
Phương pháp giải:
Sử dụng kiến thức giá của vectơ để chứng minh: Đường thẳng đi qua điểm đầu và điểm cuối của vectơ được gọi là giá của vectơ đó.
Lời giải chi tiết:
a) Mối quan hệ của góc \(\left( {\Delta ,\left( P \right)} \right)\) và \(\left( {\Delta ,\Delta '} \right)\) là: \(\left( {\Delta ,\left( P \right)} \right) = {90^0} - \left( {\Delta ,\Delta '} \right)\)
b) Ta có: +) \(\left( {\Delta ,\left( P \right)} \right) = {90^0} - \left( {\Delta ,\Delta '} \right) = {90^0} - \left( {\overrightarrow u ,\overrightarrow n } \right)\) với \(\left( {\overrightarrow u ,\overrightarrow n } \right) \le {90^o}\)
+) \(\left( {\Delta ,\left( P \right)} \right) = {90^0} - \left( {\Delta ,\Delta '} \right) = {90^0} - \left[ {{{180}^o} - \left( {\overrightarrow u ,\overrightarrow n } \right)} \right] = - {90^o} + \left( {\overrightarrow u ,\overrightarrow n } \right)\) với \(\left( {\overrightarrow u ,\overrightarrow n } \right) > {90^o}\)
Suy ra, \(\sin \left( {\Delta ,\Delta '} \right) = \left| {\cos \left( {\overrightarrow u ,\overrightarrow n } \right)} \right|\).
Trả lời câu hỏi Luyện tập 2 trang 51 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, tính góc giữa đường thẳng \(\Delta \) và mặt phẳng (P), với:
\(\Delta :\frac{{x + 2}}{{ - 1}} = \frac{{y - 4}}{2} = \frac{{z + 1}}{1},\left( P \right):x - y + z - 1 = 0\).
Phương pháp giải:
Sử dụng kiến thức về góc giữa đường thẳng và mặt phẳng để tính: Trong không gian Oxyz, cho đường thẳng \(\Delta \) có vectơ chỉ phương \(\overrightarrow u = \left( {a;b;c} \right)\) và mặt phẳng (P) có vectơ pháp tuyến \(\overrightarrow n = \left( {A;B;C} \right)\).
Khi đó: \(\sin \left( {\Delta ,\left( P \right)} \right) = \left| {\cos \left( {\overrightarrow u ,\overrightarrow n } \right)} \right| = \frac{{\left| {aA + bB + cC} \right|}}{{\sqrt {{a^2} + {b^2} + {c^2}} .\sqrt {{A^2} + {B^2} + {C^2}} }}\)
Lời giải chi tiết:
Đường thẳng \(\Delta \) có vectơ chỉ phương \(\overrightarrow u = \left( { - 1;2;1} \right)\), mặt phẳng (P) có vectơ pháp tuyến \(\overrightarrow n = \left( {1; - 1;1} \right)\). Ta có: \(\sin \left( {\Delta ,\left( P \right)} \right) = \frac{{\left| {\left( { - 1} \right).1 + 2.\left( { - 1} \right) + 1.1} \right|}}{{\sqrt {{{\left( { - 1} \right)}^2} + {2^2} + {1^2}} .\sqrt {{1^2} + {{\left( { - 1} \right)}^2} + {1^2}} }} = \frac{{\sqrt 2 }}{3}\)
Do đó, góc giữa đường thẳng \(\Delta \) và mặt phẳng (P) khoảng \(28,{1^0}\).
Trả lời câu hỏi Hoạt động 2 trang 51 SGK Toán 12 Kết nối tri thức
Trong không gian Oxyz, cho đường thẳng \(\Delta \) và mặt phẳng (P). Xét \(\overrightarrow u = \left( {a;b;c} \right)\) là một vectơ chỉ phương của \(\Delta \) và \(\overrightarrow n = \left( {A;B;C} \right)\) (với giá \(\Delta '\)) là một vectơ pháp tuyến của (P). (H.5.35)
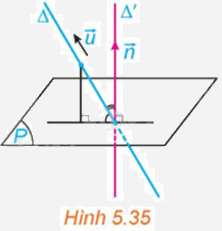
a) Hãy tìm mối quan hệ giữa các góc \(\left( {\Delta ,\left( P \right)} \right)\) và \(\left( {\Delta ,\Delta '} \right)\).
b) Có nhận xét gì về mối quan hệ giữa \(\sin \left( {\Delta ,\Delta '} \right)\) và \(\left| {\cos \left( {\overrightarrow u ,\overrightarrow n } \right)} \right|\)?
Phương pháp giải:
Sử dụng kiến thức giá của vectơ để chứng minh: Đường thẳng đi qua điểm đầu và điểm cuối của vectơ được gọi là giá của vectơ đó.
Lời giải chi tiết:
a) Mối quan hệ của góc \(\left( {\Delta ,\left( P \right)} \right)\) và \(\left( {\Delta ,\Delta '} \right)\) là: \(\left( {\Delta ,\left( P \right)} \right) = {90^0} - \left( {\Delta ,\Delta '} \right)\)
b) Ta có: +) \(\left( {\Delta ,\left( P \right)} \right) = {90^0} - \left( {\Delta ,\Delta '} \right) = {90^0} - \left( {\overrightarrow u ,\overrightarrow n } \right)\) với \(\left( {\overrightarrow u ,\overrightarrow n } \right) \le {90^o}\)
+) \(\left( {\Delta ,\left( P \right)} \right) = {90^0} - \left( {\Delta ,\Delta '} \right) = {90^0} - \left[ {{{180}^o} - \left( {\overrightarrow u ,\overrightarrow n } \right)} \right] = - {90^o} + \left( {\overrightarrow u ,\overrightarrow n } \right)\) với \(\left( {\overrightarrow u ,\overrightarrow n } \right) > {90^o}\)
Suy ra, \(\sin \left( {\Delta ,\Delta '} \right) = \left| {\cos \left( {\overrightarrow u ,\overrightarrow n } \right)} \right|\).
Mục 2 trang 51 SGK Toán 12 tập 2 - Kết nối tri thức thường xoay quanh các chủ đề về đạo hàm, ứng dụng của đạo hàm trong việc khảo sát hàm số, và các bài toán liên quan đến cực trị, giá trị lớn nhất, giá trị nhỏ nhất của hàm số. Việc nắm vững kiến thức nền tảng về đạo hàm là vô cùng quan trọng để giải quyết các bài tập trong mục này.
Để hiểu rõ hơn về Mục 2 trang 51, chúng ta cần xem xét các nội dung chính sau:
Dưới đây là giải chi tiết một số bài tập tiêu biểu trong Mục 2 trang 51 SGK Toán 12 tập 2 - Kết nối tri thức:
Giải:
f'(x) = 3x^2 - 4x + 5
Giải:
y' = 3x^2 - 6x
Giải phương trình y' = 0, ta được x = 0 hoặc x = 2.
Xét dấu y', ta thấy:
Vậy hàm số đạt cực đại tại x = 0, y = 2 và đạt cực tiểu tại x = 2, y = -2.
Giải:
y' = -2x + 4
Giải phương trình y' = 0, ta được x = 2.
Tính giá trị của hàm số tại các điểm đầu mút của đoạn và tại điểm dừng:
Vậy giá trị lớn nhất của hàm số trên đoạn [-1; 3] là 1 và giá trị nhỏ nhất là -6.
Để giải các bài tập về đạo hàm một cách hiệu quả, bạn nên:
Ngoài SGK Toán 12 tập 2 - Kết nối tri thức, bạn có thể tham khảo thêm các tài liệu sau:
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức và kỹ năng cần thiết để giải quyết các bài tập trong Mục 2 trang 51 SGK Toán 12 tập 2 - Kết nối tri thức. Chúc bạn học tập tốt!