Bài tập 3.17 trang 86 SGK Toán 12 tập 1 thuộc chương trình học Toán 12 Kết nối tri thức. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập 3.17, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Trong bài thực hành đo hiệu điện thế của mạch điện, An và Bình đã dùng hai vôn kế khác nhau để đo, mỗi bạn tiến hành đo 10 lần cho kết quả như sau: Tính độ lệch chuẩn của các mẫu số liệu ghép nhóm cho kết quả số đo của An và Bình. Từ đó kết luận xem vôn kết của bạn nào cho kết quả ổn định hơn.
Đề bài
Trong bài thực hành đo hiệu điện thế của mạch điện, An và Bình đã dùng hai vôn kế khác nhau để đo, mỗi bạn tiến hành đo 10 lần cho kết quả như sau: 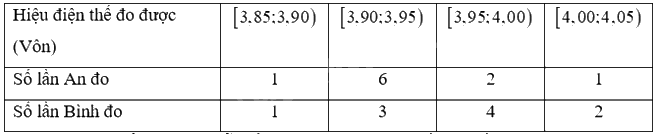
Tính độ lệch chuẩn của các mẫu số liệu ghép nhóm cho kết quả số đo của An và Bình. Từ đó kết luận xem vôn kết của bạn nào cho kết quả ổn định hơn.
Phương pháp giải - Xem chi tiết
+ Sử dụng kiến thức về phương sai của mẫu số liệu ghép nhóm để tính: Phương sai của mẫu số liệu ghép nhóm, kí hiệu là \({s^2}\), là một số được tính theo công thức sau: \({s^2} = \frac{1}{n}\left( {{m_1}x_1^2 + ... + {m_k}x_k^2} \right) - {\left( {\overline x } \right)^2}\), trong đó \(n = {m_1} + ... + {m_k}\) với \(\overline x = \frac{{{m_1}{x_1} + ... + {m_k}{x_k}}}{n}\) là số trung bình của mẫu số liệu ghép nhóm.
+ Sử dụng kiến thức độ lệch chuẩn của mẫu số liệu ghép nhóm để tính: Độ lệch chuẩn của mẫu số liệu ghép nhóm, kí hiệu là s, là căn bậc hai số học của phương sai của mẫu số liệu ghép nhóm, tức là \(s = \sqrt {{s^2}} \).
+ Sử dụng kiến thức về nghĩa của độ lệch chuẩn để đưa ra kết luận: Nếu độ lệch chuẩn càng lớn thì mẫu số liệu càng phân tán.
Lời giải chi tiết
Mẫu số liệu với giá trị đại diện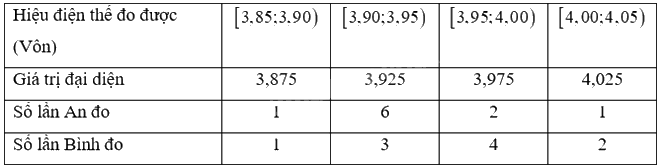
Kết quả đo của An:
Giá trị trung bình: \(\overline {{x_1}} = \frac{1}{{10}}\left( {3,875.1 + 3,925.6 + 3,975.2 + 4,025.1} \right) = 3,94\)
Phương sai của mẫu số liệu:
\({s_1}^2 = \frac{1}{{10}}\left( {3,{{875}^2}.1 + 3,{{925}^2}.6 + 3,{{975}^2}.2 + 4,{{025}^2}.1} \right) - 3,{94^2} = 0,001525\)
Độ lệch chuẩn của mẫu số liệu: \({s_1} = \sqrt {0,001525} \approx 0,039\)
Kết quả đo của Bình:
Giá trị trung bình: \(\overline {{x_1}} = \frac{1}{{10}}\left( {3,875.1 + 3,925.3 + 3,975.4 + 4,025.4} \right) = 3,96\)
Phương sai của mẫu số liệu:
\({s_2}^2 = \frac{1}{{10}}\left( {3,{{875}^2}.1 + 3,{{925}^2}.3 + 3,{{975}^2}.4 + 4,{{025}^2}.2} \right) - 3,{96^2} = 0,002025\)
Độ lệch chuẩn của mẫu số liệu: \({s_2} = \sqrt {0,002025} \approx 0,045\)
Vì \({s_2} > {s_1}\) nên Vôn kế của bạn An cho kết quả ổn định hơn.
Bài tập 3.17 SGK Toán 12 tập 1 Kết nối tri thức yêu cầu học sinh giải quyết một bài toán liên quan đến việc tìm đạo hàm và ứng dụng đạo hàm để khảo sát hàm số. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các kiến thức cơ bản về đạo hàm, bao gồm:
Trước khi bắt đầu giải bài tập, chúng ta cần đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Thông thường, bài tập 3.17 sẽ yêu cầu chúng ta:
Để giải bài tập 3.17, chúng ta sẽ thực hiện các bước sau:
Giả sử hàm số f(x) = x3 - 3x2 + 2. Chúng ta sẽ áp dụng các bước trên để giải bài tập:
Bài tập 3.17 trang 86 SGK Toán 12 tập 1 Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của nó. Bằng cách nắm vững các kiến thức cơ bản và thực hành giải nhiều bài tập tương tự, các em học sinh sẽ tự tin hơn trong việc giải quyết các bài toán Toán 12.