Giải bài tập 9 trang 91 SGK Toán 12 tập 2 - Kết nối tri thức

Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 12. Bài viết này sẽ hướng dẫn bạn giải bài tập 9 trang 91 SGK Toán 12 tập 2 - Kết nối tri thức một cách nhanh chóng và hiệu quả.

Chúng tôi cam kết mang đến cho bạn những giải pháp học tập tốt nhất, giúp bạn nắm vững kiến thức và đạt kết quả cao trong môn Toán.

Cho tứ diện ABCD, gọi G là trọng tâm của tam giác BCD và M là trung điểm của đoạn thẳng AG. Khi đó \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} \) bằng A. \(\overrightarrow {MG} \). B. \(2\overrightarrow {MG} \). C. \(3\overrightarrow {MG} \). D. \(4\overrightarrow {MG} \).

Đề bài

A. \(\overrightarrow {MG} \).

B. \(2\overrightarrow {MG} \).

C. \(3\overrightarrow {MG} \).

D. \(4\overrightarrow {MG} \).

Phương pháp giải - Xem chi tiết Giải bài tập 9 trang 91 SGK Toán 12 tập 2 - Kết nối tri thức 1

Sử dụng kiến thức về quy tắc ba điểm để tính: Nếu A, B, C là ba điểm bất kì thì \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)

Sử dụng kiến thức về hệ thức vectơ về trọng tâm của tam giác để tính: Nếu G là trọng tâm của tam giác ABC thì \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \)

Lời giải chi tiết

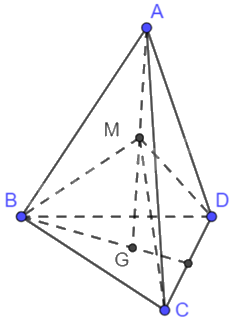
Giải bài tập 9 trang 91 SGK Toán 12 tập 2 - Kết nối tri thức 2

Vì M là trung điểm của AG nên \(\overrightarrow {MA} = - \overrightarrow {MG} \).

Vì G là trọng tâm của tam giác BCD nên \(\overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \)

Ta có: \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} = - \overrightarrow {MG} + \overrightarrow {MG} + \overrightarrow {GB} + \overrightarrow {MG} + \overrightarrow {GC} + \overrightarrow {MG} + \overrightarrow {GD} \)

\( = 2\overrightarrow {MG} + \left( {\overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} } \right) = 2\overrightarrow {MG} \)

Chọn B

Tự tin bứt phá Kỳ thi THPT Quốc gia môn Toán! Đừng bỏ lỡ Giải bài tập 9 trang 91 SGK Toán 12 tập 2 - Kết nối tri thức đặc sắc thuộc chuyên mục đề toán lớp 12 trên nền tảng toán học. Với bộ bài tập toán trung học phổ thông được biên soạn chuyên sâu, bám sát cấu trúc đề thi và chương trình Toán 12, đây chính là "chiến lược vàng" giúp các em tối ưu hóa ôn luyện. Học sinh sẽ không chỉ làm chủ mọi dạng bài thi mà còn nắm vững chiến thuật làm bài hiệu quả, sẵn sàng tự tin chinh phục điểm cao, vững bước vào đại học mơ ước nhờ phương pháp học trực quan, khoa học và hiệu quả học tập vượt trội!

Giải bài tập 9 trang 91 SGK Toán 12 tập 2 - Kết nối tri thức: Tổng quan

Bài tập 9 trang 91 SGK Toán 12 tập 2 thuộc chương trình học về Đạo hàm. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm của hàm số để giải quyết các bài toán thực tế. Việc nắm vững kiến thức về đạo hàm là vô cùng quan trọng, không chỉ cho kỳ thi THPT Quốc gia mà còn là nền tảng cho các môn học khác ở bậc đại học.

Nội dung bài tập 9 trang 91 SGK Toán 12 tập 2 - Kết nối tri thức

Bài tập 9 thường có dạng như sau: Cho hàm số f(x). Tính đạo hàm f'(x) và sử dụng đạo hàm để giải các bài toán liên quan đến tính đơn điệu, cực trị của hàm số, hoặc các bài toán ứng dụng thực tế.

Phương pháp giải bài tập 9 trang 91 SGK Toán 12 tập 2 - Kết nối tri thức

Xác định hàm số: Đọc kỹ đề bài để xác định chính xác hàm số f(x) cần xét.
Tính đạo hàm: Sử dụng các quy tắc tính đạo hàm đã học (đạo hàm của tổng, hiệu, tích, thương, hàm hợp,...) để tính đạo hàm f'(x).
Phân tích đạo hàm: Nghiên cứu dấu của f'(x) để xác định khoảng đồng biến, nghịch biến của hàm số.
Tìm cực trị: Giải phương trình f'(x) = 0 để tìm các điểm cực trị của hàm số.
Giải quyết bài toán: Sử dụng đạo hàm và các kết quả đã tìm được để giải quyết bài toán cụ thể trong đề bài.

Ví dụ minh họa giải bài tập 9 trang 91 SGK Toán 12 tập 2 - Kết nối tri thức

Ví dụ: Cho hàm số f(x) = x³ - 3x² + 2. Tìm khoảng đồng biến, nghịch biến và cực trị của hàm số.

Giải:

Tính đạo hàm: f'(x) = 3x² - 6x
Phân tích đạo hàm: f'(x) = 0 ⇔ 3x² - 6x = 0 ⇔ x(x - 2) = 0 ⇔ x = 0 hoặc x = 2
Xác định khoảng đồng biến, nghịch biến:
- Khi x < 0: f'(x) > 0 ⇒ Hàm số đồng biến trên (-∞; 0)
- Khi 0 < x < 2: f'(x) < 0 ⇒ Hàm số nghịch biến trên (0; 2)
- Khi x > 2: f'(x) > 0 ⇒ Hàm số đồng biến trên (2; +∞)
Tìm cực trị:
- Tại x = 0: f'(x) đổi dấu từ dương sang âm ⇒ Hàm số đạt cực đại tại x = 0, giá trị cực đại là f(0) = 2
- Tại x = 2: f'(x) đổi dấu từ âm sang dương ⇒ Hàm số đạt cực tiểu tại x = 2, giá trị cực tiểu là f(2) = -2

Lưu ý khi giải bài tập 9 trang 91 SGK Toán 12 tập 2 - Kết nối tri thức

Luôn kiểm tra lại các bước tính đạo hàm để tránh sai sót.
Phân tích đạo hàm một cách cẩn thận để xác định chính xác khoảng đồng biến, nghịch biến và cực trị của hàm số.
Sử dụng các công cụ hỗ trợ như máy tính bỏ túi hoặc phần mềm toán học để kiểm tra kết quả.
Luyện tập thường xuyên để nắm vững kiến thức và kỹ năng giải bài tập.

Tài liệu tham khảo

Ngoài SGK Toán 12 tập 2 - Kết nối tri thức, bạn có thể tham khảo thêm các tài liệu sau:

Sách bài tập Toán 12
Các trang web học Toán online uy tín
Các video hướng dẫn giải bài tập Toán 12 trên YouTube

Kết luận

Bài tập 9 trang 91 SGK Toán 12 tập 2 - Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm và rèn luyện kỹ năng giải toán. Hy vọng với hướng dẫn chi tiết và ví dụ minh họa trên, bạn sẽ tự tin giải quyết bài tập này một cách hiệu quả. Chúc bạn học tập tốt!