Bài tập 1.29 trang 41 SGK Toán 12 tập 1 thuộc chương trình học Toán 12 Kết nối tri thức. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế. Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Chúng tôi luôn cập nhật nhanh chóng và chính xác các lời giải bài tập Toán 12, đáp ứng nhu cầu học tập của học sinh trên toàn quốc.
Giả sử hàm cầu đối với một loại hàng hóa được cho bởi công thức \(p = \frac{{354}}{{1 + 0,01x}},x \ge 0\), trong đó p là giá bán (nghìn đồng) của mỗi đơn vị sản phẩm và x là số lượng đơn vị sản phẩm đã bán. a) Tìm công thức tính x như là hàm số của p. Tìm tập xác định của hàm số này. Tính số đơn vị sản phẩm đã bán khi giá bán của mỗi đơn vị sản phẩm là 240 nghìn đồng. b) Khảo sát sự biến thiên và vẽ đồ thị của hàm số \(x = x\left( p \right)\). Từ đồ thị đã vẽ, hãy cho biết: - Số lượng đơn vị
Đề bài
Giả sử hàm cầu đối với một loại hàng hóa được cho bởi công thức \(p = \frac{{354}}{{1 + 0,01x}},x \ge 0\), trong đó p là giá bán (nghìn đồng) của mỗi đơn vị sản phẩm và x là số lượng đơn vị sản phẩm đã bán.a) Tìm công thức tính x như là hàm số của p. Tìm tập xác định của hàm số này. Tính số đơn vị sản phẩm đã bán khi giá bán của mỗi đơn vị sản phẩm là 240 nghìn đồng.b) Khảo sát sự biến thiên và vẽ đồ thị của hàm số \(x = x\left( p \right)\). Từ đồ thị đã vẽ, hãy cho biết:- Số lượng đơn vị sản phẩm bán được sẽ thay đổi thế nào khi giá bán p tăng;- Ý nghĩa thực tiễn của giới hạn \(\mathop {\lim }\limits_{p \to {0^ + }} x\left( p \right)\).
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về sơ đồ khảo sát hàm số phân thức để khảo sát và vẽ đồ thị hàm số:
Sơ đồ khảo sát hàm số phân thức
1. Tìm tập xác định của hàm số.
2. Khảo sát sự biến thiên của hàm số:
+ Tính đạo hàm y’. Tìm các điểm tại đó y’ bằng 0 hoặc đạo hàm không tồn tại.
+ Xét dấu y’ để chỉ ra các khoảng đơn điệu của hàm số.
+ Tìm cực trị của hàm số.
+ Tìm các giới hạn tại vô cực, giới hạn vô cực và tìm tiệm cận của đồ thị hàm số.
+ Lập bảng biến thiên của hàm số.
3. Vẽ đồ thị của hàm số dựa vào bảng biến thiên
Lời giải chi tiết
a) Tìm công thức tính x như là hàm số của p. Tìm tập xác định của hàm số này. Tính số đơn vị sản phẩm đã bán khi giá bán của mỗi đơn vị sản phẩm là 240 nghìn đồng.
Vì \(p = \frac{{354}}{{1 + 0,01x}} \Rightarrow p\left( {1 + 0,01x} \right) = 354 \Rightarrow p + 0,01px = 354 \Rightarrow x = \frac{{354 - p}}{{0,01p}}\)
Tập xác định của hàm số là: \(\left( {0;354} \right]\)
Với \(p = 240\) ta có: \(x = \frac{{354 - 240}}{{0,01.240}} = 47,5\)
Vậy với giá bán mỗi đơn vị sản phẩm là 240 nghìn đồng thì bán được 47,5 đơn vị sản phẩm.
b) Khảo sát sự biến thiên của hàm số: \(x = x\left( p \right) = \frac{{354 - p}}{{0,01p}}\)
1. Tập xác định của hàm số: \(\left( {0;354} \right]\)
2. Sự biến thiên:
Ta có: \(x'\left( p \right) = \frac{{ - 3,54}}{{{{\left( {0,01p} \right)}^2}}} < 0\) với mọi \(p \in \left( {0;354} \right]\).
Hàm số nghịch biến trên khoảng \(\left( {0;354} \right)\).
Hàm số không có cực trị.
Giới hạn: \(\mathop {\lim }\limits_{p \to {0^ + }} x\left( p \right) = \mathop {\lim }\limits_{p \to {0^ + }} \frac{{354 - p}}{{0,01p}} = + \infty \)
Do đó, đồ thị hàm số \(x = x\left( p \right) = \frac{{354 - p}}{{0,01p}}\) với \(p \in \left( {0;354} \right]\) nhận đường thẳng \(p = 0\) làm tiệm cận đứng.
Bảng biến thiên:
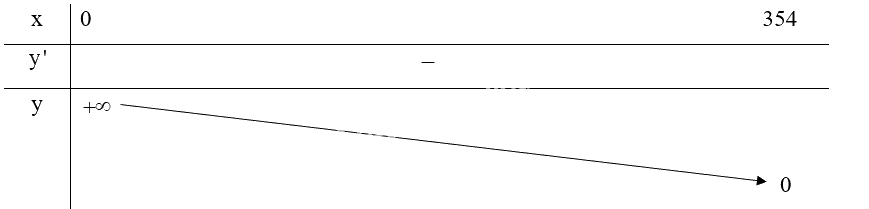
3. Đồ thị:
Ta có: \(f\left( p \right) = 0 \Leftrightarrow \frac{{354 - p}}{{0,01p}} = 0 \Leftrightarrow p = 354\)
Đồ thị hàm số \(x = f\left( p \right) = \frac{{354 - p}}{{0,01p}}\) cắt trục hoành tại điểm (354; 0).
Đồ thị hàm số \(x = f\left( p \right) = \frac{{354 - p}}{{0,01p}}\) đi qua các điểm (300; 18); (200; 77).
Đồ thị hàm số \(x = f\left( p \right) = \frac{{354 - p}}{{0,01p}}\) với \(p \in \left( {0;354} \right]\) là đường màu xanh:
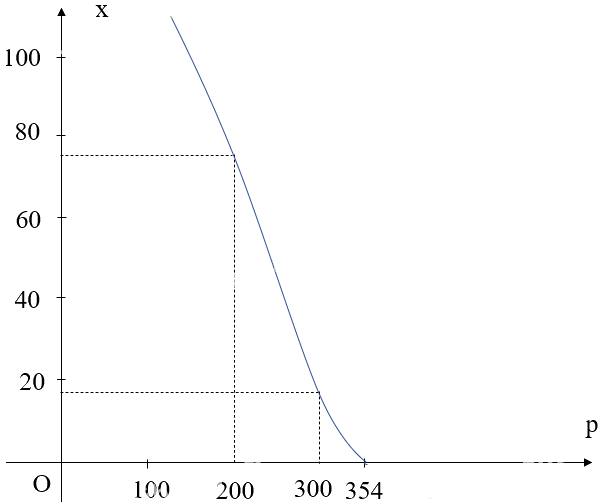
- Số lượng đơn vị sản phẩm bán sẽ giảm đi khi giá bán tăng, và sẽ không bán được sản phẩm nào nếu giá bán là 354 nghìn đồng
- Ý nghĩa thực tiễn của giới hạn \(\mathop {\lim }\limits_{p \to {0^ + }} x\left( p \right)\): Vì \(\mathop {\lim }\limits_{p \to {0^ + }} x\left( p \right) = + \infty \) nên giá bán càng thấp thì số lượng đơn vị sản phẩm sẽ bán được càng nhiều.
Bài tập 1.29 SGK Toán 12 tập 1 Kết nối tri thức yêu cầu học sinh giải quyết một bài toán thực tế liên quan đến việc tính đạo hàm và ứng dụng đạo hàm để tìm giá trị lớn nhất, giá trị nhỏ nhất của một hàm số. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các kiến thức sau:
Đề bài: (Giả sử đề bài cụ thể của bài tập 1.29 được đưa ra ở đây. Ví dụ: Một vật chuyển động theo phương trình s(t) = t3 - 3t2 + 5t + 2. Tính vận tốc của vật tại thời điểm t = 2.)
Để giải bài tập này, chúng ta thực hiện các bước sau:
Ví dụ minh họa:
Nếu đề bài là: Một vật chuyển động theo phương trình s(t) = t3 - 3t2 + 5t + 2. Tính vận tốc của vật tại thời điểm t = 2.
Lời giải:
Vận tốc của vật tại thời điểm t là đạo hàm của hàm s(t) theo t:
v(t) = s'(t) = 3t2 - 6t + 5
Thay t = 2 vào v(t), ta được:
v(2) = 3(2)2 - 6(2) + 5 = 12 - 12 + 5 = 5
Vậy vận tốc của vật tại thời điểm t = 2 là 5.
Ngoài bài tập 1.29, SGK Toán 12 tập 1 Kết nối tri thức còn có nhiều bài tập tương tự liên quan đến ứng dụng đạo hàm. Các bài tập này thường yêu cầu học sinh:
Để làm tốt các bài tập này, học sinh cần luyện tập thường xuyên và nắm vững các kiến thức cơ bản về đạo hàm và ứng dụng đạo hàm.
Dưới đây là một số mẹo giúp bạn giải bài tập về đạo hàm và ứng dụng đạo hàm hiệu quả:
Giaitoan.edu.vn hy vọng với lời giải chi tiết và hướng dẫn cụ thể này, các em học sinh sẽ tự tin hơn khi giải bài tập 1.29 trang 41 SGK Toán 12 tập 1 - Kết nối tri thức và các bài tập tương tự. Chúc các em học tập tốt!
| Hàm số | Đạo hàm |
|---|---|
| y = c (hằng số) | y' = 0 |
| y = xn | y' = nxn-1 |
| y = sinx | y' = cosx |
| y = cosx | y' = -sinx |