Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 7 tập 2 - Chân trời sáng tạo. Bài viết này sẽ hướng dẫn bạn từng bước giải bài 3 trang 40, giúp bạn nắm vững kiến thức và tự tin hơn trong học tập.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập hiệu quả nhất, đồng thời giúp bạn hiểu rõ bản chất của từng bài toán. Hãy cùng bắt đầu với bài 3 trang 40 nhé!
Thực hiện phép chia.
Đề bài
Thực hiện phép chia.
a) \((8{x^6} - 4{x^5} + 12{x^4} - 20{x^3}):4{x^3}\)
b) \((2{x^2} - 5x + 3):(2x - 3)\)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Thực hiện phép nhân chia đa thức bằng cách đặt tính.
Chú ý: Sắp xếp thứ tự đa thức theo giảm dần của lũy thừa
Lời giải chi tiết
a) \((8{x^6} - 4{x^5} + 12{x^4} - 20{x^3}):4{x^3}\)
\( = (8{x^6}:4{x^3}) - (4{x^5}:4{x^3}) + (12{x^4}:4{x^3}) - (20{x^3}:4{x^3})\)
\( = 2{x^3} - {x^2} + 3x - 5\)
b)
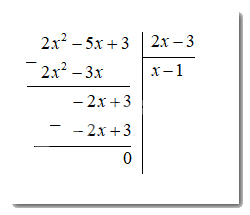
Vậy \((2{x^2} - 5x + 3):(2x - 3)= x - 1\)
Bài 3 trang 40 SGK Toán 7 tập 2 - Chân trời sáng tạo thuộc chương trình học về các góc và mối quan hệ giữa các góc tạo bởi một đường thẳng cắt hai đường thẳng song song. Để giải bài tập này, học sinh cần nắm vững các kiến thức sau:
Đề bài: (Sách giáo khoa Toán 7 tập 2 - Chân trời sáng tạo)
Quan sát Hình 3 và cho biết:
Giải:
a) Hai đường thẳng a và b có song song không? Vì sao?
Ta thấy góc A1 và góc B1 là một cặp góc so le trong. Nếu góc A1 = góc B1 thì hai đường thẳng a và b song song (theo tiên đề Euclid).
Trong hình, ta có góc A1 = 60o và góc B1 = 60o. Do đó, góc A1 = góc B1.
Vậy, hai đường thẳng a và b song song.
b) Tính số đo góc B1.
Như đã giải thích ở phần a, góc B1 = góc A1 = 60o.
Các bài tập liên quan đến việc xác định hai đường thẳng song song thường yêu cầu học sinh:
Để giải các bài tập này, bạn nên:
Để củng cố kiến thức, bạn có thể tự giải các bài tập sau:
Bài 3 trang 40 SGK Toán 7 tập 2 - Chân trời sáng tạo là một bài tập quan trọng giúp học sinh hiểu rõ hơn về các góc và mối quan hệ giữa chúng. Hy vọng với lời giải chi tiết và các hướng dẫn trên, bạn đã có thể tự tin giải bài tập này và các bài tập tương tự. Chúc bạn học tốt!