Chào mừng các em học sinh đến với lời giải chi tiết mục 2 trang 38, 39 SGK Toán 7 tập 2 - Chân trời sáng tạo trên giaitoan.edu.vn. Bài viết này sẽ cung cấp đáp án đầy đủ, chính xác và dễ hiểu cho từng bài tập, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi hiểu rằng việc giải bài tập Toán đôi khi có thể gặp khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn lời giải một cách cẩn thận, kèm theo các bước giải chi tiết và giải thích rõ ràng.
Thực hiện phép nhân
Thực hiện phép nhân \((3x + 1)({x^2} - 2x + 1)\), rồi đoán xem \((3{x^3} - 5{x^2} + x + 1):(3x + 1)\) bằng đa thức nào.
Phương pháp giải:
Lời giải chi tiết:
\(\begin{array}{l}(3x + 1)({x^2} - 2x + 1)\\ = 3x({x^2} - 2x + 1) + 1({x^2} - 2x + 1)\\ = 3{x^3} - 6{x^2} + 3x + {x^2} - 2x + 1\\ = 3{x^3} - 5{x^2} + x + 1\end{array}\)
Vì \((3x + 1)({x^2} - 2x + 1) = 3{x^3} - 5{x^2} + x + 1\)
\( \Rightarrow (3{x^3} - 5{x^2} + x + 1):(3x + 1) = {x^2} - 2x + 1\)
Thực hiện phép chia P(x) = \((6{x^2} + 4x)\) cho Q(x) = 2x
Phương pháp giải:
Lời giải chi tiết:
\((6{x^2} + 4x):2x = (6{x^2}:2x) + (4x:2x)\)
\( = 3x + 2\)
Thực hiện các phép chia sau \(\frac{{9{x^2} + 5x + x}}{{3x}}\) và \(\frac{{(2{x^2} - 4x) + (x - 2)}}{{2 - x}}\)
Phương pháp giải:
Lời giải chi tiết:
\(\frac{{9{x^2} + 5x + x}}{{3x}} = \frac{{9{x^2} + 6x}}{{3x}} = \frac{{9{x^2}}}{{3x}} + \frac{{6x}}{{3x}} = 3x + 2\)
\(\frac{{2{x^2} - 3x - 2}}{{2 - x}} = \frac{{2{x^2} - 3x - 2}}{{ - x + 2}} = - 2x - 1\)
Thực hiện phép chia \(({x^2} + 5x + 9):(x + 2)\)
Phương pháp giải:
Ta sử dụng qui tắc chia 2 đa thức
Lời giải chi tiết:
\(({x^2} + 2x + 9):(x + 2) = \frac{{{x^2} + 5x + 9}}{{3x + 6}} = x + 3 + \frac{3}{{x + 2}}\) ta có :
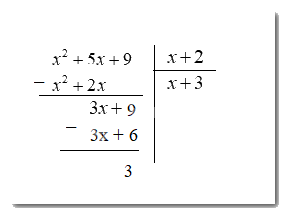
Vậy \( = x + 3 + \frac{3}{{x + 2}}\)
Video hướng dẫn giải
Thực hiện phép nhân \((3x + 1)({x^2} - 2x + 1)\), rồi đoán xem \((3{x^3} - 5{x^2} + x + 1):(3x + 1)\) bằng đa thức nào.
Phương pháp giải:
Lời giải chi tiết:
\(\begin{array}{l}(3x + 1)({x^2} - 2x + 1)\\ = 3x({x^2} - 2x + 1) + 1({x^2} - 2x + 1)\\ = 3{x^3} - 6{x^2} + 3x + {x^2} - 2x + 1\\ = 3{x^3} - 5{x^2} + x + 1\end{array}\)
Vì \((3x + 1)({x^2} - 2x + 1) = 3{x^3} - 5{x^2} + x + 1\)
\( \Rightarrow (3{x^3} - 5{x^2} + x + 1):(3x + 1) = {x^2} - 2x + 1\)
Thực hiện phép chia P(x) = \((6{x^2} + 4x)\) cho Q(x) = 2x
Phương pháp giải:
Lời giải chi tiết:
\((6{x^2} + 4x):2x = (6{x^2}:2x) + (4x:2x)\)
\( = 3x + 2\)
Thực hiện các phép chia sau \(\frac{{9{x^2} + 5x + x}}{{3x}}\) và \(\frac{{(2{x^2} - 4x) + (x - 2)}}{{2 - x}}\)
Phương pháp giải:
Lời giải chi tiết:
\(\frac{{9{x^2} + 5x + x}}{{3x}} = \frac{{9{x^2} + 6x}}{{3x}} = \frac{{9{x^2}}}{{3x}} + \frac{{6x}}{{3x}} = 3x + 2\)
\(\frac{{2{x^2} - 3x - 2}}{{2 - x}} = \frac{{2{x^2} - 3x - 2}}{{ - x + 2}} = - 2x - 1\)
Thực hiện phép chia \(({x^2} + 5x + 9):(x + 2)\)
Phương pháp giải:
Ta sử dụng qui tắc chia 2 đa thức
Lời giải chi tiết:
\(({x^2} + 2x + 9):(x + 2) = \frac{{{x^2} + 5x + 9}}{{3x + 6}} = x + 3 + \frac{3}{{x + 2}}\) ta có :
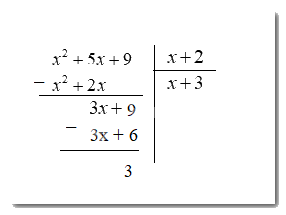
Vậy \( = x + 3 + \frac{3}{{x + 2}}\)
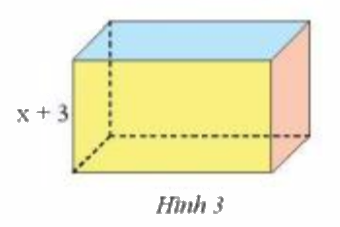
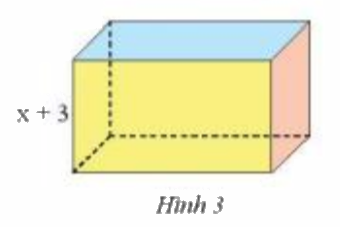
Tính diện tích đáy của một hình hộp chữ nhật (Hình 3) có chiều cao bằng (x + 3) cm và có thể tích bằng \(({x^3} + 8{x^2} + 19x + 12)\)\(c{m^3}\)
Phương pháp giải:
Lời giải chi tiết:
\( \Rightarrow ({x^3} + 8{x^2} + 19x + 12):(x + 3) =\) diện tích đáy
Ta có :
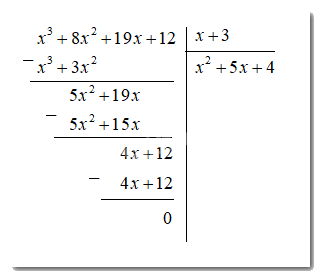
Vậy diện tích đáy là : \({x^2} + 5x + 4\) \(c{m^2}\)
Tính diện tích đáy của một hình hộp chữ nhật (Hình 3) có chiều cao bằng (x + 3) cm và có thể tích bằng \(({x^3} + 8{x^2} + 19x + 12)\)\(c{m^3}\)
Phương pháp giải:
Lời giải chi tiết:
\( \Rightarrow ({x^3} + 8{x^2} + 19x + 12):(x + 3) =\) diện tích đáy
Ta có :

Vậy diện tích đáy là : \({x^2} + 5x + 4\) \(c{m^2}\)
Mục 2 của chương trình Toán 7 tập 2 - Chân trời sáng tạo tập trung vào việc ôn tập và củng cố các kiến thức về số hữu tỉ, phép cộng, trừ, nhân, chia số hữu tỉ, và các tính chất của các phép toán này. Việc nắm vững kiến thức này là nền tảng quan trọng để học tốt các chương tiếp theo.
Bài tập 1 yêu cầu học sinh thực hiện các phép tính cộng, trừ, nhân, chia số hữu tỉ. Để giải bài tập này, học sinh cần nắm vững các quy tắc về dấu của số hữu tỉ và các phép toán. Ví dụ:
Bài tập 2 thường liên quan đến việc áp dụng các tính chất của phép cộng, trừ, nhân, chia số hữu tỉ để tính toán nhanh chóng và hiệu quả. Ví dụ, tính chất giao hoán, kết hợp, phân phối có thể được sử dụng để đơn giản hóa các biểu thức.
Bài tập 3 có thể yêu cầu học sinh giải các bài toán thực tế liên quan đến số hữu tỉ. Để giải các bài toán này, học sinh cần phân tích đề bài, xác định các dữ kiện và yêu cầu, và sử dụng các kiến thức đã học để tìm ra lời giải.
Giả sử chúng ta cần giải bài tập sau: Tính (1/2) + (2/3) - (1/4). Chúng ta có thể thực hiện như sau:
Việc luyện tập thường xuyên là yếu tố quan trọng để nắm vững kiến thức và kỹ năng giải bài tập Toán. Hãy dành thời gian để làm các bài tập trong SGK, sách bài tập, và các đề thi thử. Đồng thời, hãy tìm hiểu các phương pháp giải bài tập khác nhau để có thể áp dụng linh hoạt trong các tình huống khác nhau.
Hy vọng rằng bài viết này đã cung cấp cho các em học sinh những kiến thức và kỹ năng cần thiết để giải mục 2 trang 38, 39 SGK Toán 7 tập 2 - Chân trời sáng tạo một cách hiệu quả. Chúc các em học tập tốt!
| Bài tập | Nội dung chính |
|---|---|
| Bài 1 | Thực hiện các phép tính cộng, trừ, nhân, chia số hữu tỉ. |
| Bài 2 | Áp dụng các tính chất của phép toán để tính toán nhanh chóng. |
| Bài 3 | Giải các bài toán thực tế liên quan đến số hữu tỉ. |