Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 1 trang 48, 49 SGK Toán 7 tập 2 chương trình Chân trời sáng tạo. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu cùng với phương pháp giải bài tập một cách khoa học.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, tự tin giải quyết các bài toán Toán 7 và đạt kết quả tốt nhất trong học tập.
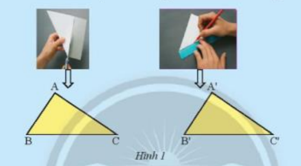
Dùng kéo cắt một tờ giấy thành hình tam giác ABC. Đặt tam giác lên tờ giấy thứ hai. Vẽ và cắt theo các cạnh của tam giác ABC thành tam giác A’B’C’ (Hình1). Hãy so sánh các cạnh và các góc của hai tam giác ABC và A’B’C’
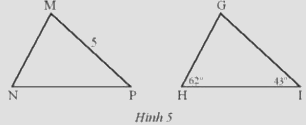
Trong Hình 5, cho biết . Hãy tính số đo góc M và độ dài cạnh GI.
Phương pháp giải:
Áp dụng các tính chất của 2 tam giác bằng nhau
Lời giải chi tiết:
Theo định lí tổng 3 góc trong tam giác ta có :
\(\widehat G + \widehat H + \widehat I = {180^o} \Rightarrow \widehat G = {180^o} - {62^o} - {43^o} = {75^o}\)
Vì \(\Delta MNP =\Delta GHI \Rightarrow \widehat G = \widehat M\) (2 góc tương ứng)
\( \Rightarrow \widehat M = {75^o}\)
\(\Delta MNP =\Delta GHI \Rightarrow MP=GI \) (2 cạnh tương ứng)
\(\Rightarrow GI=5 cm\).
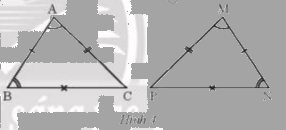
Quan sát Hình 4. Hai tam giác ABC và MNP có bằng nhau không? Hãy chỉ ra các cặp góc và các cặp cạnh tương ứng bằng nhau.
Phương pháp giải:
Ta dựa vào định nghĩa về 2 tam giác bằng nhau
Lời giải chi tiết:
\( \Rightarrow \Delta{ABC}=\Delta{MNP}\) do có các cặp góc và cạnh tương ứng bằng nhau.
Các cặp góc bằng nhau là: \(\widehat A = \widehat M\); \(\widehat B = \widehat N\);\(\widehat C = \widehat P\)
Các cặp cạnh bằng nhau là: \(AB = MN; AC = MP; BC = PN\)
Dùng kéo cắt một tờ giấy thành hình tam giác ABC. Đặt tam giác lên tờ giấy thứ hai. Vẽ và cắt theo các cạnh của tam giác ABC thành tam giác A’B’C’ (Hình1). Hãy so sánh các cạnh và các góc của hai tam giác ABC và A’B’C’.
Phương pháp giải:
Ta cắt 2 tam giác như hướng dẫn
Lời giải chi tiết:
Ta thấy 2 tam giác có các cặp góc bằng nhau \(\widehat A = \widehat {A'}\); \(\widehat B = \widehat {B'}\); \(\widehat C = \widehat {C'}\)
2 tam giác có các cặp cạnh bằng nhau AC = A’C’; AB = A’B’; BC = B’C’
Video hướng dẫn giải
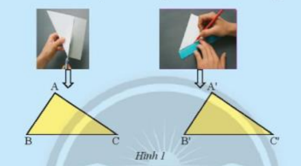
Dùng kéo cắt một tờ giấy thành hình tam giác ABC. Đặt tam giác lên tờ giấy thứ hai. Vẽ và cắt theo các cạnh của tam giác ABC thành tam giác A’B’C’ (Hình1). Hãy so sánh các cạnh và các góc của hai tam giác ABC và A’B’C’.
Phương pháp giải:
Ta cắt 2 tam giác như hướng dẫn
Lời giải chi tiết:
Ta thấy 2 tam giác có các cặp góc bằng nhau \(\widehat A = \widehat {A'}\); \(\widehat B = \widehat {B'}\); \(\widehat C = \widehat {C'}\)
2 tam giác có các cặp cạnh bằng nhau AC = A’C’; AB = A’B’; BC = B’C’
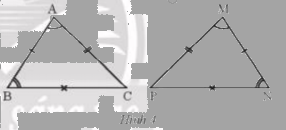
Quan sát Hình 4. Hai tam giác ABC và MNP có bằng nhau không? Hãy chỉ ra các cặp góc và các cặp cạnh tương ứng bằng nhau.
Phương pháp giải:
Ta dựa vào định nghĩa về 2 tam giác bằng nhau
Lời giải chi tiết:
\( \Rightarrow \Delta{ABC}=\Delta{MNP}\) do có các cặp góc và cạnh tương ứng bằng nhau.
Các cặp góc bằng nhau là: \(\widehat A = \widehat M\); \(\widehat B = \widehat N\);\(\widehat C = \widehat P\)
Các cặp cạnh bằng nhau là: \(AB = MN; AC = MP; BC = PN\)
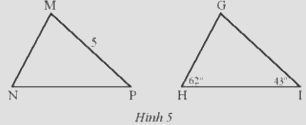
Trong Hình 5, cho biết . Hãy tính số đo góc M và độ dài cạnh GI.
Phương pháp giải:
Áp dụng các tính chất của 2 tam giác bằng nhau
Lời giải chi tiết:
Theo định lí tổng 3 góc trong tam giác ta có :
\(\widehat G + \widehat H + \widehat I = {180^o} \Rightarrow \widehat G = {180^o} - {62^o} - {43^o} = {75^o}\)
Vì \(\Delta MNP =\Delta GHI \Rightarrow \widehat G = \widehat M\) (2 góc tương ứng)
\( \Rightarrow \widehat M = {75^o}\)
\(\Delta MNP =\Delta GHI \Rightarrow MP=GI \) (2 cạnh tương ứng)
\(\Rightarrow GI=5 cm\).
Mục 1 trang 48, 49 SGK Toán 7 tập 2 Chân trời sáng tạo tập trung vào việc ôn tập và củng cố các kiến thức về số hữu tỉ, phép cộng, trừ, nhân, chia số hữu tỉ. Các bài tập trong mục này thường yêu cầu học sinh vận dụng các quy tắc, tính chất đã học để thực hiện các phép tính, so sánh và sắp xếp các số hữu tỉ.
Bài tập này yêu cầu học sinh thực hiện các phép tính cộng, trừ, nhân, chia số hữu tỉ. Để giải bài tập này, học sinh cần nắm vững các quy tắc về dấu của số hữu tỉ, quy tắc cộng, trừ, nhân, chia số hữu tỉ. Ví dụ:
Bài tập này yêu cầu học sinh so sánh các số hữu tỉ. Để giải bài tập này, học sinh có thể quy đồng mẫu số của các số hữu tỉ hoặc chuyển các số hữu tỉ về dạng số thập phân để so sánh. Ví dụ:
Bài tập này yêu cầu học sinh tìm giá trị của x thỏa mãn một phương trình hoặc bất phương trình. Để giải bài tập này, học sinh cần vận dụng các quy tắc biến đổi phương trình hoặc bất phương trình. Ví dụ:
Khi giải bài tập về số hữu tỉ, học sinh cần chú ý các điểm sau:
Kiến thức về số hữu tỉ và các phép toán trên số hữu tỉ có ứng dụng rộng rãi trong đời sống và các lĩnh vực khoa học khác. Ví dụ, số hữu tỉ được sử dụng để biểu diễn các đại lượng như chiều dài, diện tích, thể tích, thời gian, tiền bạc,...
Hy vọng với lời giải chi tiết và phương pháp giải bài tập được trình bày trên đây, các em học sinh sẽ tự tin hơn khi giải các bài tập về số hữu tỉ trong SGK Toán 7 tập 2 Chân trời sáng tạo. Chúc các em học tập tốt!