Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 7 tập 2 theo chương trình Chân trời sáng tạo. Bài viết này sẽ giúp bạn giải quyết triệt để các vấn đề trong mục 1 trang 64, đảm bảo bạn nắm vững kiến thức và tự tin hơn trong học tập.
Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn lời giải chi tiết, kèm theo các bước giải thích rõ ràng, giúp bạn hiểu bản chất của bài toán.
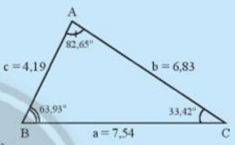
Cho tam giác ABC trong Hình 1. - Hãy sắp xếp theo thứ tự từ nhỏ đến lớn độ dài của ba cạnh a,b,c - Hãy sắp xếp theo thứ tự từ nhỏ đến lớn độ lớn độ lớn của ba góc A,B,C là các góc đối diện với ba cạnh a,b,c. - Nêu nhận xét của em về hai kết quả sắp xếp trên.
Cho tam giác ABC trong Hình 1.
- Hãy sắp xếp theo thứ tự từ nhỏ đến lớn độ dài của ba cạnh a,b,c
- Hãy sắp xếp theo thứ tự từ nhỏ đến lớn độ lớn độ lớn của ba góc A,B,C là các góc đối diện với ba cạnh a,b,c.
- Nêu nhận xét của em về hai kết quả sắp xếp trên.
Phương pháp giải:
Ta dựa cào số đo các cạnh, góc của tam giác để sắp xếp theo độ lớn
Lời giải chi tiết:
- Độ dài các cạnh từ nhỏ đến lớn là c, b, a
- Các góc từ nhỏ đến lớn là C, B, A
- Ta thấy trong tam giác ABC cạnh đối diện với góc lớn hơn thì lớn hơn và ngược lại.
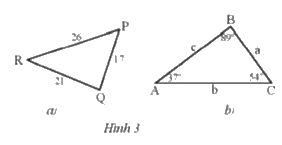
a) Sắp xếp theo thứ tự từ nhỏ đến lớn số đo các góc của tam giác PQR trong Hình 3a.
b) Sắp xếp theo thứ tự từ nhỏ đến lớn độ dài các cạnh của tam giác ABC trong Hình 3b.
Phương pháp giải:
Sử dụng định lí về góc đối diện cạnh trong tam giác
Lời giải chi tiết:
a) Ta có độ dài các cạnh tam giác PQR theo thứ tự từ nhỏ đến lớn là PQ, QR, RP
Vì trong tam giác góc đối diện cạnh lớn hơn thì lớn hơn
Nên ra có các góc tam giác PQR theo thứ tự từ nhỏ đến lớn là R, P, Q
b) Ta có số đo các góc theo tứ tự từ nhỏ đến lớn của tam giác ABC là A, C, B
Vì trong tam giác góc đối diện cạnh lớn hơn thì lớn hơn
Nên ta có các cạnh tam giác ABC theo thứ tự từ nhỏ đến lớn là a, c, b.
a) Cho tam giác DEF có góc F là góc tù. Cạnh nào là cạnh có độ dài lớn nhất trong ba cạnh của tam giác DEF ?
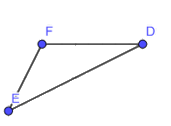
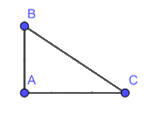
b) Cho tam giác ABC vuông tại A. Cạnh nào là cạnh có độ dài lớn nhất trong ba cạnh của tam giác ABC ?
Phương pháp giải:
Sử dụng tính chất góc đối diện và cạnh trong tam giác
Lời giải chi tiết:
a) Vì tổng số đo 3 góc trong tam giác là 180° mà F là góc tù
Suy ra F > 90° do F là góc tù
hay D + E < 180° - 90°
nên F là góc lớn nhất trong tam giác DEF
Vì vậy cạnh đối diện góc F sẽ là cạnh lớn nhất tam giác DEF hay DE là cạnh lớn nhất
b) Tam giác ABC có góc A là góc vuông nên ta có: \( \widehat B + \widehat C = {90^o} \)
suy ra \(\widehat B;\widehat C < {90^o}\)
nên A là góc lớn nhất tam giác ABC
suy ra BC là cạnh lớn nhất tam giác ABC do đối diện góc A
Video hướng dẫn giải
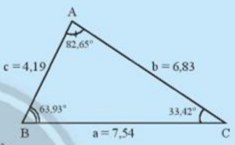
Cho tam giác ABC trong Hình 1.
- Hãy sắp xếp theo thứ tự từ nhỏ đến lớn độ dài của ba cạnh a,b,c
- Hãy sắp xếp theo thứ tự từ nhỏ đến lớn độ lớn độ lớn của ba góc A,B,C là các góc đối diện với ba cạnh a,b,c.
- Nêu nhận xét của em về hai kết quả sắp xếp trên.
Phương pháp giải:
Ta dựa cào số đo các cạnh, góc của tam giác để sắp xếp theo độ lớn
Lời giải chi tiết:
- Độ dài các cạnh từ nhỏ đến lớn là c, b, a
- Các góc từ nhỏ đến lớn là C, B, A
- Ta thấy trong tam giác ABC cạnh đối diện với góc lớn hơn thì lớn hơn và ngược lại.
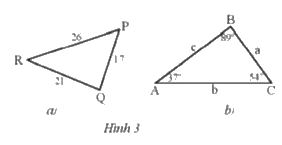
a) Sắp xếp theo thứ tự từ nhỏ đến lớn số đo các góc của tam giác PQR trong Hình 3a.
b) Sắp xếp theo thứ tự từ nhỏ đến lớn độ dài các cạnh của tam giác ABC trong Hình 3b.
Phương pháp giải:
Sử dụng định lí về góc đối diện cạnh trong tam giác
Lời giải chi tiết:
a) Ta có độ dài các cạnh tam giác PQR theo thứ tự từ nhỏ đến lớn là PQ, QR, RP
Vì trong tam giác góc đối diện cạnh lớn hơn thì lớn hơn
Nên ra có các góc tam giác PQR theo thứ tự từ nhỏ đến lớn là R, P, Q
b) Ta có số đo các góc theo tứ tự từ nhỏ đến lớn của tam giác ABC là A, C, B
Vì trong tam giác góc đối diện cạnh lớn hơn thì lớn hơn
Nên ta có các cạnh tam giác ABC theo thứ tự từ nhỏ đến lớn là a, c, b.
a) Cho tam giác DEF có góc F là góc tù. Cạnh nào là cạnh có độ dài lớn nhất trong ba cạnh của tam giác DEF ?
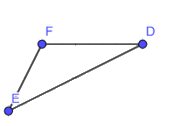
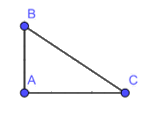
b) Cho tam giác ABC vuông tại A. Cạnh nào là cạnh có độ dài lớn nhất trong ba cạnh của tam giác ABC ?
Phương pháp giải:
Sử dụng tính chất góc đối diện và cạnh trong tam giác
Lời giải chi tiết:
a) Vì tổng số đo 3 góc trong tam giác là 180° mà F là góc tù
Suy ra F > 90° do F là góc tù
hay D + E < 180° - 90°
nên F là góc lớn nhất trong tam giác DEF
Vì vậy cạnh đối diện góc F sẽ là cạnh lớn nhất tam giác DEF hay DE là cạnh lớn nhất
b) Tam giác ABC có góc A là góc vuông nên ta có: \( \widehat B + \widehat C = {90^o} \)
suy ra \(\widehat B;\widehat C < {90^o}\)
nên A là góc lớn nhất tam giác ABC
suy ra BC là cạnh lớn nhất tam giác ABC do đối diện góc A
Mục 1 trang 64 SGK Toán 7 tập 2 - Chân trời sáng tạo thường tập trung vào một chủ đề cụ thể trong chương trình học. Để giải quyết các bài tập trong mục này, học sinh cần nắm vững các khái niệm, định nghĩa và tính chất liên quan. Bài viết này sẽ đi sâu vào phân tích từng bài tập, cung cấp lời giải chi tiết và giải thích rõ ràng để giúp bạn hiểu rõ hơn về kiến thức đã học.
Bài 1 trong mục 1 trang 64 thường là bài tập áp dụng trực tiếp các kiến thức đã học. Để giải bài này, bạn cần:
Ví dụ, nếu bài tập yêu cầu tính giá trị của một biểu thức, bạn cần thay các giá trị đã cho vào biểu thức và thực hiện các phép tính theo đúng thứ tự ưu tiên.
Bài 2 thường là bài tập nâng cao, yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các vấn đề phức tạp hơn. Để giải bài này, bạn cần:
Ví dụ, nếu bài tập yêu cầu chứng minh một đẳng thức, bạn cần sử dụng các phép biến đổi đại số để đưa đẳng thức về dạng đơn giản nhất.
Bài 3 thường là bài tập luyện tập, giúp học sinh củng cố kiến thức và rèn luyện kỹ năng giải toán. Để giải bài này, bạn cần:
Khi giải bài tập Toán 7 tập 2 - Chân trời sáng tạo, bạn cần lưu ý một số điều sau:
Bài 1: (Giả sử đề bài là tính giá trị của biểu thức 2x + 3y khi x = 1 và y = 2)
Lời giải:
Thay x = 1 và y = 2 vào biểu thức 2x + 3y, ta được:
2 * 1 + 3 * 2 = 2 + 6 = 8
Vậy giá trị của biểu thức 2x + 3y khi x = 1 và y = 2 là 8.
Bài 2: (Giả sử đề bài là chứng minh đẳng thức a + b = b + a)
Lời giải:
Đẳng thức a + b = b + a là một tính chất cơ bản của phép cộng. Theo tính chất giao hoán của phép cộng, thứ tự của các số hạng không ảnh hưởng đến kết quả của phép cộng. Do đó, a + b = b + a luôn đúng.
Hy vọng rằng bài viết này đã cung cấp cho bạn những kiến thức và kỹ năng cần thiết để giải quyết các bài tập trong mục 1 trang 64 SGK Toán 7 tập 2 - Chân trời sáng tạo. Hãy luyện tập thường xuyên để nâng cao khả năng giải toán của bạn. Chúc bạn học tập tốt!