Chào mừng các em học sinh đến với lời giải chi tiết mục 2 trang 78, 79 sách giáo khoa Toán 7 tập 1 chương trình Chân trời sáng tạo. Bài viết này sẽ cung cấp đáp án đầy đủ và cách giải các bài tập trong mục, giúp các em hiểu rõ kiến thức và rèn luyện kỹ năng giải toán.
giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán. Hãy cùng chúng tôi khám phá lời giải chi tiết ngay sau đây!
Cho điểm A nằm ngoài đường thẳng a, quan sát cách vẽ đường thẳng b đi qua A và song song với a ở Hình 8...a) Cho tam giác ABC. Hãy nêu cách vẽ đường thẳng a đi qua A và song song với BC, vẽ đường thẳng b đi qua B và song song với AC. b) Có thể vẽ được bao nhiêu đường thẳng a, bao nhiêu đường thẳng b? Vì sao?
a) Cho tam giác ABC. Hãy nêu cách vẽ đường thẳng a đi qua A và song song với BC, vẽ đường thẳng b đi qua B và song song với AC.
b) Có thể vẽ được bao nhiêu đường thẳng a, bao nhiêu đường thẳng b? Vì sao?
Phương pháp giải:
+ Vẽ đường thẳng a đi qua A sao cho a và BC tạo với đường thẳng AB cặp góc so le trong bằng nhau.
+ Vẽ đường thẳng b đi qua B sao cho b và AC tạo với đường thẳng BC cặp góc so le trong bằng nhau.
Lời giải chi tiết:
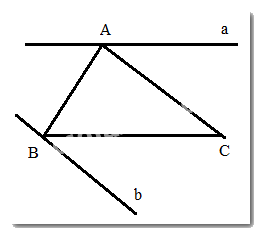
Đo góc ABC. Vẽ đường thẳng a đi qua A sao cho góc tạo bởi a và đường thẳng AB bằng góc ABC.
Ta được đường thẳng a đi qua A và song song với BC
Đo góc ACB. Vẽ đường thẳng b đi qua B sao cho góc tạo bởi b và đường thẳng BC bằng góc ACB.
Ta được đường thẳng b đi qua B và song song với AC
b) Có thể vẽ được chỉ 1 đường thẳng a, 1 đường thẳng b thoả mãn yêu cầu. Vì qua 1 điểm nằm ngoài một đường thẳng, chỉ có 1 đường thẳng song song với nó
Cho điểm A nằm ngoài đường thẳng a, quan sát cách vẽ đường thẳng b đi qua A và song song với a ở Hình 8
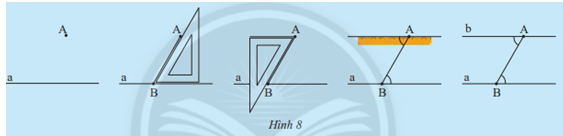
Em hãy dự đoán xem có bao nhiêu đường thẳng b đi qua A và song song với đường thẳng a
Phương pháp giải:
Từ cách vẽ trên, em vẽ được bao nhiêu đường thẳng b đi qua A và song song với a
Lời giải chi tiết:
Có chỉ 1 đường thẳng b đi qua A và song song với đường thẳng a
Video hướng dẫn giải
Cho điểm A nằm ngoài đường thẳng a, quan sát cách vẽ đường thẳng b đi qua A và song song với a ở Hình 8
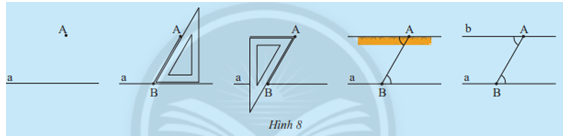
Em hãy dự đoán xem có bao nhiêu đường thẳng b đi qua A và song song với đường thẳng a
Phương pháp giải:
Từ cách vẽ trên, em vẽ được bao nhiêu đường thẳng b đi qua A và song song với a
Lời giải chi tiết:
Có chỉ 1 đường thẳng b đi qua A và song song với đường thẳng a
a) Cho tam giác ABC. Hãy nêu cách vẽ đường thẳng a đi qua A và song song với BC, vẽ đường thẳng b đi qua B và song song với AC.
b) Có thể vẽ được bao nhiêu đường thẳng a, bao nhiêu đường thẳng b? Vì sao?
Phương pháp giải:
+ Vẽ đường thẳng a đi qua A sao cho a và BC tạo với đường thẳng AB cặp góc so le trong bằng nhau.
+ Vẽ đường thẳng b đi qua B sao cho b và AC tạo với đường thẳng BC cặp góc so le trong bằng nhau.
Lời giải chi tiết:
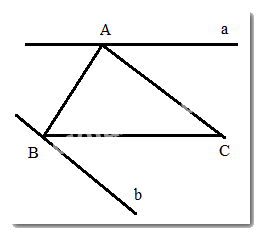
Đo góc ABC. Vẽ đường thẳng a đi qua A sao cho góc tạo bởi a và đường thẳng AB bằng góc ABC.
Ta được đường thẳng a đi qua A và song song với BC
Đo góc ACB. Vẽ đường thẳng b đi qua B sao cho góc tạo bởi b và đường thẳng BC bằng góc ACB.
Ta được đường thẳng b đi qua B và song song với AC
b) Có thể vẽ được chỉ 1 đường thẳng a, 1 đường thẳng b thoả mãn yêu cầu. Vì qua 1 điểm nằm ngoài một đường thẳng, chỉ có 1 đường thẳng song song với nó
Mục 2 trang 78, 79 SGK Toán 7 tập 1 - Chân trời sáng tạo tập trung vào việc vận dụng các kiến thức về số hữu tỉ, phép cộng, trừ, nhân, chia số hữu tỉ để giải quyết các bài toán thực tế. Các bài tập trong mục này thường yêu cầu học sinh phải hiểu rõ các quy tắc, tính chất của các phép toán và biết cách áp dụng chúng một cách linh hoạt.
Bài tập này yêu cầu học sinh thực hiện các phép tính cộng, trừ, nhân, chia số hữu tỉ. Để giải bài tập này, học sinh cần nắm vững các quy tắc về dấu của số hữu tỉ, quy tắc cộng, trừ, nhân, chia số hữu tỉ và biết cách thực hiện các phép tính một cách chính xác.
Bài tập này yêu cầu học sinh giải các phương trình đơn giản với số hữu tỉ. Để giải bài tập này, học sinh cần nắm vững các quy tắc về chuyển vế, quy đồng mẫu số và biết cách giải phương trình một cách chính xác.
Bài tập này yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế. Để giải bài tập này, học sinh cần đọc kỹ đề bài, xác định các dữ kiện và yêu cầu của bài toán, sau đó áp dụng các kiến thức đã học để giải quyết bài toán.
Ví dụ: Một người nông dân có một mảnh đất hình chữ nhật, chiều dài là 10m, chiều rộng là 5m. Người nông dân muốn trồng rau trên mảnh đất đó. Hỏi người nông dân cần bao nhiêu mét vuông đất để trồng rau?
Giải: Diện tích mảnh đất hình chữ nhật là: 10m * 5m = 50m2. Vậy người nông dân cần 50m2 đất để trồng rau.
Ngoài sách giáo khoa, học sinh có thể tham khảo thêm các tài liệu sau để học tập và rèn luyện kỹ năng giải toán:
Hy vọng rằng với lời giải chi tiết và hướng dẫn cụ thể trong bài viết này, các em học sinh sẽ hiểu rõ hơn về mục 2 trang 78, 79 SGK Toán 7 tập 1 - Chân trời sáng tạo và có thể tự tin giải quyết các bài tập tương tự. Chúc các em học tập tốt!