Chào mừng các em học sinh đến với lời giải chi tiết mục 3 trang 55, 56, 57 sách giáo khoa Toán 7 tập 2 chương trình Chân trời sáng tạo. Bài viết này sẽ cung cấp đáp án và hướng dẫn giải bài tập một cách dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán.
Hãy nêu các trường hợp bằng nhau cho mỗi cặp tam giác trong Hình 17. Từ các điều kiện bằng nhau của hai tam giác, người ta suy ra được các trường hợp bằng nhau sau đây của hai tam giác vuông.
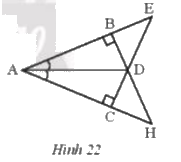
Hãy chỉ ra các cặp tam giác bằng nhau trong Hình 22 và cho biết chúng bằng nhau theo trường hợp nào.
Phương pháp giải:
- Sử dụng các trường hợp bằng nhau của tam giác: c-c-c; c-g-c; g-c-g
- Sử dụng các trường hợp bằng nhau của tam giác vuông: 2 cạnh góc vuông; cạnh góc vuông - góc nhọn kề; cạnh huyền - góc nhọn.
Lời giải chi tiết:
+) Xét \(\Delta{ABD}\) vuông tại B và \(\Delta{ACD}\) vuông tại D có:
AD chung
\(\widehat {BAD} = \widehat {DAC}\) (gt)
\( \Rightarrow \Delta{ABD}=\Delta{ACD}\) (cạnh huyền – góc nhọn)
\( \Rightarrow \) BD = CD, AB = AC ( 2 cạnh tương ứng)
\( \widehat {BDA} = \widehat {ADC}\)( 2 góc tương ứng)
+) Xét \(\Delta{BED}\) vuông tại B và \(\Delta{CHD}\) vuông tại C có:
BD = CD (cmt)
\(\widehat {BDE} = \widehat {CDH}\)( 2 góc đối đỉnh )
\( \Rightarrow \Delta{BED}=\Delta{CHD}\) (cạnh góc vuông - góc nhọn kề )
+) Ta có: \(\widehat {BDA} + \widehat {BDE}\)= \(\widehat {ADE}\)
\(\widehat {ADC} + \widehat {CDH}\)= \(\widehat {ADH}\)
Mà \(\widehat {BDA} = \widehat {ADC}\), \(\widehat {BDE} = \widehat {CDH}\)
\( \Rightarrow \widehat {ADE} = \widehat {ADH}\)
Xét \(\Delta{ADE}\) và \(\Delta{ADH}\) có:
\(\widehat {BAD} = \widehat {DAC}\) (gt)
AD chung
\(\widehat {ADE} = \widehat {ADH}\) (cmt)
\( \Rightarrow \Delta{ADE}=\Delta{ADH}\)( g – c – g )
+) Xét \(\Delta{ABH}\) vuông tại B và \(\Delta{ACE}\) vuông tại C có:
AB = AC (cmt)
\(\widehat {BAH}\) chung
\( \Rightarrow \Delta{ABH}=\Delta{ACE}\) (cạnh góc vuông – góc nhọn kề)
Tìm các tam giác vuông bằng nhau trong mỗi hình bên (Hình 19).

Phương pháp giải:
Sử dụng các trường hợp bằng nhau của tam giác vuông
Lời giải chi tiết:
a) Xét \(\Delta{MNP} và \Delta{QPN}\), ta có:
NM = PQ
NP chung
\(\widehat {MNP} = \widehat {NPQ}\)
\(\Rightarrow \Delta{MNP} =\Delta{QPN}\) (c.g.c)
b) Ta thấy\(\Delta{ABH}=\Delta{KBH}\) (g-c-g) và \(\Delta{AHC}=\Delta{KHC}\)(c-g-c)
\(\Delta{ABC}=\Delta{KBC}\)
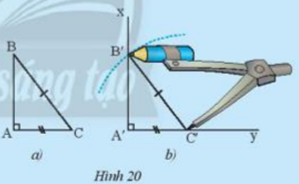
Cho tam giác ABC vuông tại A trong Hình 20a. Vẽ lên tờ giấy tam giác vuông A’B’C’có cạnh huyền và một cạnh góc vuông bằng với cạnh huyền và một cạnh góc vuông của tam giác ABC như sau:
- Vẽ góc vuông xA’ý, trên cạnh A’y vẽ đoạn A’C’= AC.
- Vẽ cung tròn tâm C’ bán kính bằng BC cắt A’x tại B’
Cắt rời tam giác A’B’C’. Em hãy cho biết có thể đặt chồng khít tam giác này lên tam giác kia không.
Phương pháp giải:
- Ta vẽ 2 cạnh trước rồi sau đó vẽ góc
- Cắt và so sánh 2 hình
Lời giải chi tiết:
Ta nhận thấy 2 hình bằng nhau (chồng lên nhau vì vừa khít)
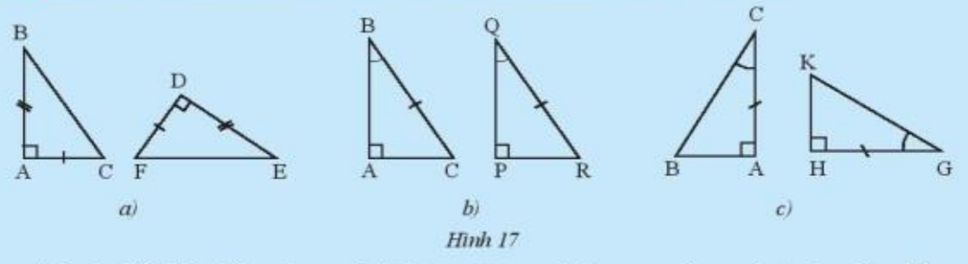
Hãy nêu các trường hợp bằng nhau cho mỗi cặp tam giác trong Hình 17. Từ các điều kiện bằng nhau của hai tam giác, người ta suy ra được các trường hợp bằng nhau sau đây của hai tam giác vuông.
Phương pháp giải:
Dựa vào tam giác vuông có sẵn 1 cặp góc bằng nhau ( góc vuông ) nên chỉ cần tìm điều kiện để các cặp cạnh, cặp góc còn lại bằng nhau
Lời giải chi tiết:
a) Xét \(\Delta{ABC}\) và \(\Delta{DEF}\) có:
AB = DE (gt)
\(\widehat {BAC} = \widehat {EDF}\) (gt)
AC = DF (gt)
\(\Rightarrow \Delta{ABC}=\Delta{DEF}\) ( c-g-c )
b) Ta có: \(\widehat B + \widehat C = \widehat Q + \widehat R = 90^0\)
Mà \(\widehat B = \widehat Q\) \( \Rightarrow \widehat C = \widehat R\)
Xét \(\Delta{ABC}\) và \(\Delta{PQR}\) có:
\(\widehat C = \widehat R\) (gt)
BC = QR (gt)
\(\widehat B = \widehat Q\) (gt)
\(\Rightarrow \Delta{ABC}=\Delta{PQR}\) ( g-c-g )
c) Xét \(\Delta{ABC}\) và \(\Delta{HKG}\) có:
\(\widehat C = \widehat G\) (gt)
AC = HG (gt)
\(\widehat A = \widehat H\) (gt)
\(\Rightarrow \Delta{ABC}=\Delta{HKG}\) ( g-c-g )
Video hướng dẫn giải
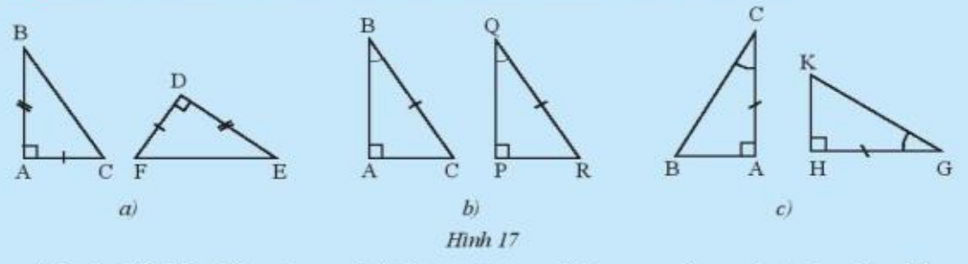
Hãy nêu các trường hợp bằng nhau cho mỗi cặp tam giác trong Hình 17. Từ các điều kiện bằng nhau của hai tam giác, người ta suy ra được các trường hợp bằng nhau sau đây của hai tam giác vuông.
Phương pháp giải:
Dựa vào tam giác vuông có sẵn 1 cặp góc bằng nhau ( góc vuông ) nên chỉ cần tìm điều kiện để các cặp cạnh, cặp góc còn lại bằng nhau
Lời giải chi tiết:
a) Xét \(\Delta{ABC}\) và \(\Delta{DEF}\) có:
AB = DE (gt)
\(\widehat {BAC} = \widehat {EDF}\) (gt)
AC = DF (gt)
\(\Rightarrow \Delta{ABC}=\Delta{DEF}\) ( c-g-c )
b) Ta có: \(\widehat B + \widehat C = \widehat Q + \widehat R = 90^0\)
Mà \(\widehat B = \widehat Q\) \( \Rightarrow \widehat C = \widehat R\)
Xét \(\Delta{ABC}\) và \(\Delta{PQR}\) có:
\(\widehat C = \widehat R\) (gt)
BC = QR (gt)
\(\widehat B = \widehat Q\) (gt)
\(\Rightarrow \Delta{ABC}=\Delta{PQR}\) ( g-c-g )
c) Xét \(\Delta{ABC}\) và \(\Delta{HKG}\) có:
\(\widehat C = \widehat G\) (gt)
AC = HG (gt)
\(\widehat A = \widehat H\) (gt)
\(\Rightarrow \Delta{ABC}=\Delta{HKG}\) ( g-c-g )
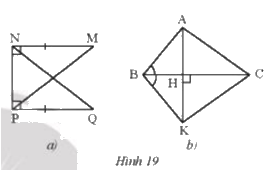
Tìm các tam giác vuông bằng nhau trong mỗi hình bên (Hình 19).
Phương pháp giải:
Sử dụng các trường hợp bằng nhau của tam giác vuông
Lời giải chi tiết:
a) Xét \(\Delta{MNP} và \Delta{QPN}\), ta có:
NM = PQ
NP chung
\(\widehat {MNP} = \widehat {NPQ}\)
\(\Rightarrow \Delta{MNP} =\Delta{QPN}\) (c.g.c)
b) Ta thấy\(\Delta{ABH}=\Delta{KBH}\) (g-c-g) và \(\Delta{AHC}=\Delta{KHC}\)(c-g-c)
\(\Delta{ABC}=\Delta{KBC}\)
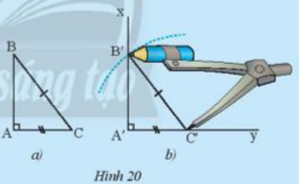
Cho tam giác ABC vuông tại A trong Hình 20a. Vẽ lên tờ giấy tam giác vuông A’B’C’có cạnh huyền và một cạnh góc vuông bằng với cạnh huyền và một cạnh góc vuông của tam giác ABC như sau:
- Vẽ góc vuông xA’ý, trên cạnh A’y vẽ đoạn A’C’= AC.
- Vẽ cung tròn tâm C’ bán kính bằng BC cắt A’x tại B’
Cắt rời tam giác A’B’C’. Em hãy cho biết có thể đặt chồng khít tam giác này lên tam giác kia không.
Phương pháp giải:
- Ta vẽ 2 cạnh trước rồi sau đó vẽ góc
- Cắt và so sánh 2 hình
Lời giải chi tiết:
Ta nhận thấy 2 hình bằng nhau (chồng lên nhau vì vừa khít)
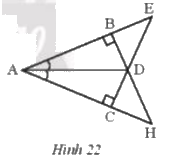
Hãy chỉ ra các cặp tam giác bằng nhau trong Hình 22 và cho biết chúng bằng nhau theo trường hợp nào.
Phương pháp giải:
- Sử dụng các trường hợp bằng nhau của tam giác: c-c-c; c-g-c; g-c-g
- Sử dụng các trường hợp bằng nhau của tam giác vuông: 2 cạnh góc vuông; cạnh góc vuông - góc nhọn kề; cạnh huyền - góc nhọn.
Lời giải chi tiết:
+) Xét \(\Delta{ABD}\) vuông tại B và \(\Delta{ACD}\) vuông tại D có:
AD chung
\(\widehat {BAD} = \widehat {DAC}\) (gt)
\( \Rightarrow \Delta{ABD}=\Delta{ACD}\) (cạnh huyền – góc nhọn)
\( \Rightarrow \) BD = CD, AB = AC ( 2 cạnh tương ứng)
\( \widehat {BDA} = \widehat {ADC}\)( 2 góc tương ứng)
+) Xét \(\Delta{BED}\) vuông tại B và \(\Delta{CHD}\) vuông tại C có:
BD = CD (cmt)
\(\widehat {BDE} = \widehat {CDH}\)( 2 góc đối đỉnh )
\( \Rightarrow \Delta{BED}=\Delta{CHD}\) (cạnh góc vuông - góc nhọn kề )
+) Ta có: \(\widehat {BDA} + \widehat {BDE}\)= \(\widehat {ADE}\)
\(\widehat {ADC} + \widehat {CDH}\)= \(\widehat {ADH}\)
Mà \(\widehat {BDA} = \widehat {ADC}\), \(\widehat {BDE} = \widehat {CDH}\)
\( \Rightarrow \widehat {ADE} = \widehat {ADH}\)
Xét \(\Delta{ADE}\) và \(\Delta{ADH}\) có:
\(\widehat {BAD} = \widehat {DAC}\) (gt)
AD chung
\(\widehat {ADE} = \widehat {ADH}\) (cmt)
\( \Rightarrow \Delta{ADE}=\Delta{ADH}\)( g – c – g )
+) Xét \(\Delta{ABH}\) vuông tại B và \(\Delta{ACE}\) vuông tại C có:
AB = AC (cmt)
\(\widehat {BAH}\) chung
\( \Rightarrow \Delta{ABH}=\Delta{ACE}\) (cạnh góc vuông – góc nhọn kề)
Mục 3 trong SGK Toán 7 tập 2 chương trình Chân trời sáng tạo thường tập trung vào một chủ đề cụ thể, đòi hỏi học sinh phải vận dụng các kiến thức đã học để giải quyết các bài toán thực tế. Việc nắm vững lý thuyết và kỹ năng giải bài tập là vô cùng quan trọng để đạt kết quả tốt trong môn học này.
Để giúp các em hiểu rõ hơn về nội dung bài tập, chúng ta sẽ đi vào phân tích từng bài tập cụ thể:
Bài tập này yêu cầu học sinh thực hiện phép tính nào đó. Để giải bài tập này, các em cần nhớ lại các quy tắc về phép tính đã học. Ví dụ, nếu bài tập yêu cầu tính tổng hai số, các em cần áp dụng quy tắc cộng hai số nguyên.
Bài tập này có thể liên quan đến việc giải phương trình hoặc bất phương trình. Để giải bài tập này, các em cần nắm vững các bước giải phương trình hoặc bất phương trình. Ví dụ, nếu bài tập yêu cầu giải phương trình x + 2 = 5, các em cần trừ cả hai vế của phương trình cho 2 để tìm ra giá trị của x.
Bài tập này có thể yêu cầu học sinh chứng minh một đẳng thức hoặc bất đẳng thức. Để giải bài tập này, các em cần sử dụng các kiến thức về đẳng thức và bất đẳng thức đã học. Ví dụ, nếu bài tập yêu cầu chứng minh a + b = b + a, các em cần sử dụng tính chất giao hoán của phép cộng.
Dưới đây là hướng dẫn giải chi tiết từng bài tập trong mục 3 trang 55, 56, 57:
Để giúp các em hiểu rõ hơn về cách giải bài tập, chúng ta sẽ xem xét một ví dụ minh họa:
Ví dụ: Giải phương trình 2x + 4 = 10
Giải:
Vậy nghiệm của phương trình là x = 3.
Hy vọng rằng với lời giải chi tiết và hướng dẫn giải bài tập trong mục 3 trang 55, 56, 57 SGK Toán 7 tập 2 chương trình Chân trời sáng tạo, các em sẽ nắm vững kiến thức và tự tin hơn trong quá trình học tập. Chúc các em học tốt!
| Công thức | Mô tả |
|---|---|
| a + b = b + a | Tính chất giao hoán của phép cộng |
| a * b = b * a | Tính chất giao hoán của phép nhân |