Bài 3 trang 75 SGK Toán 7 tập 2 thuộc chương trình Toán 7 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về các phép toán với số hữu tỉ. Bài tập này thường yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 3 trang 75 SGK Toán 7 tập 2, giúp các em học sinh nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Cho tam giác ABC. Hai đường trung tuyến AM và CN cắt nhau tại G. Trên tia đối của tia AM lấy điểm E sao cho ME = MG. a) Chứng minh rằng BG song song với EC. b) Gọi I là trung điểm của BE, AI cắt BG tại F. Chứng minh rằng AF = 2FI
Đề bài
Cho tam giác ABC. Hai đường trung tuyến AM và CN cắt nhau tại G. Trên tia đối của tia AM lấy điểm E sao cho ME = MG.
a) Chứng minh rằng BG song song với EC.
b) Gọi I là trung điểm của BE, AI cắt BG tại F. Chứng minh rằng AF = 2FI
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
- Ta dựa vào định lí ba đường trung tuyến cắt nhau tại 1 điểm. Điểm đó cách mỗi đỉnh một khoảng bằng \(\dfrac{2}{3}\)độ dài trung tuyến đi qua đỉnh ấy
- Câu a ta sẽ chứng minh 2 góc so le trong bằng nhau thông qua các tam giác bằng nhau
- Câu b ta sẽ chứng minh F là trọng tâm tam giác ABE
Lời giải chi tiết
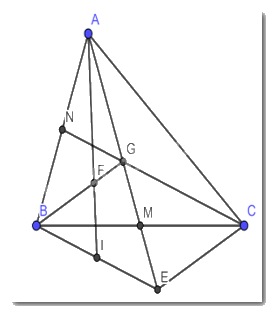
a) Xét tam giác BGM và tam giác CEM có :
\(\widehat {GMB} = \widehat {EMC}\)(2 góc đối đỉnh)
GM = ME (do G đối xứng E qua M)
MB = MC (do M là trung điểm của BC)
\( \Rightarrow \Delta BGM = \Delta CEM(c - g - c)\)
\( \Rightarrow \widehat {GBM} = \widehat {MCE}\)(2 góc tương ứng bằng nhau)
Mà 2 góc trên ở vị trí so le trong nên BG⫽CE
b) Vì I là trung điểm BE nên AI sẽ là trung tuyến của tam giác ABE
Và BG cũng là trung tuyến của tam giác ABE do G là trung điểm AE
Vì BG cắt AI tại F nên F sẽ là trọng tâm của tam giác ABE
\(\, \Rightarrow AF = \dfrac{2}{3}AI\)(định lí về trọng tâm tam giác)
Mà AI = AF + FI \( \Rightarrow \) FI = AI – AF
\( \Rightarrow FI = AI - \dfrac{2}{3}AI = \dfrac{1}{3}AI\)
\( \Rightarrow 2FI = AF = \dfrac{2}{3}AI\)
\( \Rightarrow \) AF = 2 FI
Bài 3 trang 75 SGK Toán 7 tập 2 - Chân trời sáng tạo yêu cầu học sinh thực hiện các phép tính với số hữu tỉ, bao gồm cộng, trừ, nhân, chia. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các quy tắc sau:
Dưới đây là lời giải chi tiết cho từng phần của bài 3 trang 75 SGK Toán 7 tập 2 - Chân trời sáng tạo:
Đề bài: Tính: (1/2) + (1/3)
Lời giải:
Để tính tổng (1/2) + (1/3), ta cần quy đồng mẫu số. Mẫu số chung nhỏ nhất của 2 và 3 là 6. Ta có:
(1/2) + (1/3) = (3/6) + (2/6) = (3+2)/6 = 5/6
Vậy, (1/2) + (1/3) = 5/6
Đề bài: Tính: (2/5) - (1/4)
Lời giải:
Để tính hiệu (2/5) - (1/4), ta cần quy đồng mẫu số. Mẫu số chung nhỏ nhất của 5 và 4 là 20. Ta có:
(2/5) - (1/4) = (8/20) - (5/20) = (8-5)/20 = 3/20
Vậy, (2/5) - (1/4) = 3/20
Đề bài: Tính: (3/4) * (2/7)
Lời giải:
Để tính tích (3/4) * (2/7), ta nhân các tử với nhau và nhân các mẫu với nhau:
(3/4) * (2/7) = (3*2)/(4*7) = 6/28 = 3/14
Vậy, (3/4) * (2/7) = 3/14
Đề bài: Tính: (5/6) : (1/3)
Lời giải:
Để tính thương (5/6) : (1/3), ta nhân số bị chia (5/6) với nghịch đảo của số chia (1/3). Nghịch đảo của (1/3) là 3/1.
(5/6) : (1/3) = (5/6) * (3/1) = (5*3)/(6*1) = 15/6 = 5/2
Vậy, (5/6) : (1/3) = 5/2
Để củng cố kiến thức về các phép toán với số hữu tỉ, các em có thể tự giải các bài tập tương tự sau:
Khi giải các bài tập này, các em cần chú ý quy đồng mẫu số (nếu cần) và áp dụng đúng các quy tắc cộng, trừ, nhân, chia số hữu tỉ.
Bài 3 trang 75 SGK Toán 7 tập 2 - Chân trời sáng tạo là một bài tập cơ bản nhưng quan trọng trong chương trình Toán 7. Việc nắm vững kiến thức và kỹ năng giải bài tập này sẽ giúp các em học sinh tự tin hơn trong quá trình học tập và giải quyết các bài toán phức tạp hơn.