Chào mừng các em học sinh đến với lời giải chi tiết Bài 4 trang 84 SGK Toán 7 tập 2 - Chân trời sáng tạo. Bài viết này sẽ cung cấp đáp án, phương pháp giải và giải thích rõ ràng từng bước để giúp các em hiểu bài và làm bài tập một cách hiệu quả.
giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán. Hãy cùng chúng tôi khám phá lời giải của bài tập này ngay bây giờ!
Cho tam giác ABC vuông tại A (AB < AC). Trên cạnh BC lấy điểm N sao cho BA = BN
Đề bài
Cho tam giác ABC vuông tại A (AB < AC). Trên cạnh BC lấy điểm N sao cho BA = BN. Kẻ \(BE \bot AN\)(E ∈ AN).
a) Chứng minh rằng BE là tia phân giác của giác ABN.
b) Kẻ đường cao AH của tam giác ABC. Gọi K là giao điểm của BH với CE. Chứng minh rằng NK // CA.
c) Đường thẳng BK cắt AC tại F. Gọi G là giao điểm của đường thẳng AB với NF. Chứng minh rằng tam giác GBC cân.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) Ta chứng minh \(\widehat {ABE} = \widehat {NBE}\) bằng cách chứng minh 2 tam giác BAF và BNF bằng nhau .
b) Ta chứng minh NK song song với CA do có 2 góc so le trong bằng nhau
c) Ta chứng minh góc BGC bằng góc BCG
Lời giải chi tiết
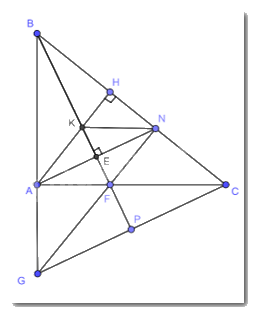
a) Xét \(\Delta BAE\) và \(\Delta BNE\) có :
BA = BN (giả thiết)
BF cạnh chung
\(\widehat {BEA} = \widehat {BEN}\)
\( \Rightarrow \Delta BAE = \Delta BNE\)(cạnh huyền-cạnh góc vuông)
\( \Rightarrow \widehat {ABF} = \widehat {NBF}\)(góc tương ứng)
\( \Rightarrow \) BE là phân giác của góc ABN
b) Vì K là giao của 2 đường cao \( \Rightarrow \)K là trực tâm tam giác ABN
\( \Rightarrow \) KN vuông góc với AB(1)
Vì CA vuông góc với AB ( tam giác ABC vuông tại A)(2)
Từ (1) và (2) \( \Rightarrow \) KN song song với CA (quan hệ cùng vuông góc với 1 đường)
c) Ta có \(\Delta BAF = \Delta BNF(c - g - c)\)do có :
\(\widehat {BEA} = \widehat {BEN}\)
BF cạnh chung
BN = BA
\( \Rightarrow \widehat {BNF} = \widehat {BAF}\) (2 góc tương ứng).
Mà \(\widehat {BAF} = 90^\circ \)
\( \Rightarrow \widehat {BNF} = \widehat {BAF} = {90^o}\)
\( \Rightarrow GN \bot BC\)
Ta có CA và GN là 2 đường cao của tam giác GBC
\( \Rightarrow \)F là trực tâm của tam giác GBC
\( \Rightarrow \)BF vuông góc với GC tại P
Xét \(\Delta BGP\) và \(\Delta BCP\) ta có :
BP cạnh chung
\(\widehat {BPC} = \widehat {BPG} = {90^o}\)
\(\widehat {PBC} = \widehat {PBG}\)
\( \Rightarrow \Delta BGP = \Delta BCP(c - g - c)\)
\( \Rightarrow BC = BG\)(2 cạnh tương ứng)
\( \Rightarrow \)Tam giác GBC cân tại B
Bài 4 trang 84 SGK Toán 7 tập 2 - Chân trời sáng tạo thuộc chương trình học Toán 7, tập trung vào việc vận dụng các kiến thức đã học về biểu thức đại số, các phép toán trên số hữu tỉ và các tính chất của chúng để giải quyết các bài toán thực tế. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản và phương pháp giải quyết bài toán.
Bài tập này thường yêu cầu học sinh thực hiện các phép tính đại số, rút gọn biểu thức, tìm giá trị của biểu thức khi biết giá trị của biến, hoặc giải các phương trình đơn giản. Ngoài ra, bài tập còn có thể yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các bài toán có tính ứng dụng cao.
Để giúp các em học sinh hiểu rõ hơn về cách giải bài tập này, chúng tôi sẽ cung cấp lời giải chi tiết từng bước. Lời giải sẽ bao gồm các bước thực hiện, giải thích rõ ràng từng bước và các lưu ý quan trọng để các em có thể tự giải quyết các bài tập tương tự.
Giả sử bài tập yêu cầu tính giá trị của biểu thức A = 2x + 3y khi x = 1 và y = -2. Chúng ta sẽ thực hiện các bước sau:
Để giải nhanh các bài tập trong Bài 4 trang 84 SGK Toán 7 tập 2 - Chân trời sáng tạo, các em cần:
Ngoài SGK Toán 7 tập 2 - Chân trời sáng tạo, các em có thể tham khảo thêm các tài liệu sau để học tập và ôn luyện:
Bài 4 trang 84 SGK Toán 7 tập 2 - Chân trời sáng tạo là một bài tập quan trọng giúp các em học sinh củng cố kiến thức và rèn luyện kỹ năng giải toán. Hy vọng rằng với lời giải chi tiết và các mẹo giải nhanh mà chúng tôi đã cung cấp, các em sẽ tự tin hơn khi giải quyết bài tập này và đạt kết quả tốt trong môn Toán.
| Khái niệm | Giải thích |
|---|---|
| Biểu thức đại số | Là một dãy các số, chữ và các phép toán. |
| Số hữu tỉ | Là số có thể biểu diễn dưới dạng phân số a/b, với a và b là các số nguyên và b khác 0. |