Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 3 trang 79, 80 SGK Toán 7 tập 1 chương trình Chân trời sáng tạo. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu cùng với phương pháp giải bài tập một cách khoa học.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, tự tin giải quyết các bài toán Toán 7 và đạt kết quả tốt nhất trong học tập.
Em hãy: - Vẽ hai đường thẳng a và b song song với nhau. - Vẽ đường thẳng c cắt đường thẳng a và b lần lượt tại A và B. a) Chọn và đo một cặp góc so le trong, so sánh cặp góc này. b) Chọn và đo một cặp góc đồng vị, so sánh cặp góc này.
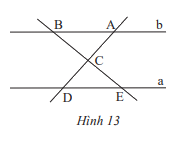
Tìm các cặp góc bằng nhau của hai tam giác ABC và DEC trong Hình 13, biết a // b.
Phương pháp giải:
*2 góc đối đỉnh thì bằng nhau
*Sử dụng tính chất của 2 đường thẳng song song: Một đường thẳng cắt hai đường thẳng song song thì:
+ 2 góc so le trong bằng nhau
+ 2 góc đồng vị bằng nhau.
Lời giải chi tiết:
Vì a // b nên \(\widehat {BAC} = \widehat {CDE};\widehat {ABC} = \widehat {CED}\) (2 góc so le trong)
Ta có: \(\widehat {ACB} = \widehat {DCE}\) ( 2 góc đối đỉnh).
Em hãy:
- Vẽ hai đường thẳng a và b song song với nhau.
- Vẽ đường thẳng c cắt đường thẳng a và b lần lượt tại A và B.
a) Chọn và đo một cặp góc so le trong, so sánh cặp góc này.
b) Chọn và đo một cặp góc đồng vị, so sánh cặp góc này.
Phương pháp giải:
Vẽ hình.
Đo và nhận xét
Lời giải chi tiết:
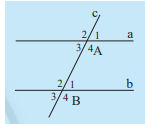
a) Một cặp góc so le trong là góc A3 và góc B1 . Hai góc này cùng có số đo là 60 \(^\circ \) nên chúng bằng nhau .
b) Một cặp góc đồng vị là góc A1 và góc B1 . Hai góc này cùng có số đo là 60 \(^\circ \) nên chúng bằng nhau .
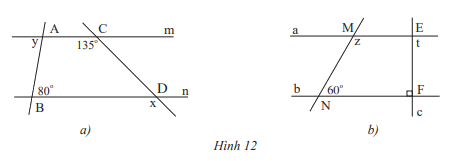
Cho biết m // n và a // b. Tính số đo x,y,z và t của các góc trong hình 12.
Phương pháp giải:
Sử dụng tính chất của 2 đường thẳng song song:
Một đường thẳng cắt hai đường thẳng song song thì:
+ 2 góc so le trong bằng nhau
+ 2 góc đồng vị bằng nhau
Lời giải chi tiết:
a) Vì m // n nên x = 135\(^\circ \)( 2 góc đồng vị) ; y = 80\(^\circ \) ( 2 góc so le trong)
b)
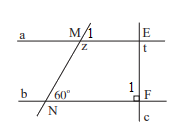
Vì a // b nên \(\widehat {{M_1}} = 60^\circ \) ( 2 góc đồng vị)
Mà \(\widehat {{M_1}} + z = 180^\circ \) ( 2 góc kề bù) nên z = 180\(^\circ \)- 60\(^\circ \)=120\(^\circ \)
Vì a // b nên \(\widehat {{F_1}} = t\) ( 2 góc so le trong), mà \(\widehat {{F_1}} = 90^\circ \) nên t = 90\(^\circ \)
Cho hai đường thẳng a, b song song với nhau, đường thẳng c vuông góc với a tại A và cắt b tại B. Hãy giải thích tại sao đường thẳng c cũng vuông góc với b.
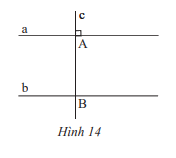
Phương pháp giải:
Sử dụng tính chất của 2 đường thẳng song song: Một đường thẳng cắt hai đường thẳng song song thì 2 góc đồng vị bằng nhau.
Lời giải chi tiết:
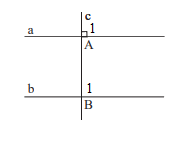
Vì a // b nên \(\widehat {{B_1}} = \widehat {{A_1}}\) (2 góc đồng vị), mà \(\widehat {{A_1}} = 90^\circ \) nên \(\widehat {{B_1}} = 90^\circ \).
Vậy c vuông góc với b.
Video hướng dẫn giải
Em hãy:
- Vẽ hai đường thẳng a và b song song với nhau.
- Vẽ đường thẳng c cắt đường thẳng a và b lần lượt tại A và B.
a) Chọn và đo một cặp góc so le trong, so sánh cặp góc này.
b) Chọn và đo một cặp góc đồng vị, so sánh cặp góc này.
Phương pháp giải:
Vẽ hình.
Đo và nhận xét
Lời giải chi tiết:
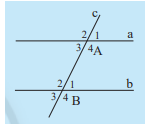
a) Một cặp góc so le trong là góc A3 và góc B1 . Hai góc này cùng có số đo là 60 \(^\circ \) nên chúng bằng nhau .
b) Một cặp góc đồng vị là góc A1 và góc B1 . Hai góc này cùng có số đo là 60 \(^\circ \) nên chúng bằng nhau .
Cho biết m // n và a // b. Tính số đo x,y,z và t của các góc trong hình 12.
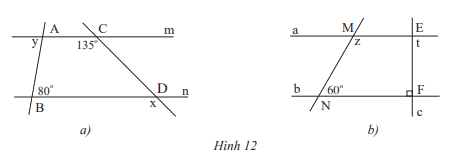
Phương pháp giải:
Sử dụng tính chất của 2 đường thẳng song song:
Một đường thẳng cắt hai đường thẳng song song thì:
+ 2 góc so le trong bằng nhau
+ 2 góc đồng vị bằng nhau
Lời giải chi tiết:
a) Vì m // n nên x = 135\(^\circ \)( 2 góc đồng vị) ; y = 80\(^\circ \) ( 2 góc so le trong)
b)
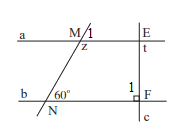
Vì a // b nên \(\widehat {{M_1}} = 60^\circ \) ( 2 góc đồng vị)
Mà \(\widehat {{M_1}} + z = 180^\circ \) ( 2 góc kề bù) nên z = 180\(^\circ \)- 60\(^\circ \)=120\(^\circ \)
Vì a // b nên \(\widehat {{F_1}} = t\) ( 2 góc so le trong), mà \(\widehat {{F_1}} = 90^\circ \) nên t = 90\(^\circ \)
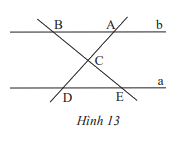
Tìm các cặp góc bằng nhau của hai tam giác ABC và DEC trong Hình 13, biết a // b.
Phương pháp giải:
*2 góc đối đỉnh thì bằng nhau
*Sử dụng tính chất của 2 đường thẳng song song: Một đường thẳng cắt hai đường thẳng song song thì:
+ 2 góc so le trong bằng nhau
+ 2 góc đồng vị bằng nhau.
Lời giải chi tiết:
Vì a // b nên \(\widehat {BAC} = \widehat {CDE};\widehat {ABC} = \widehat {CED}\) (2 góc so le trong)
Ta có: \(\widehat {ACB} = \widehat {DCE}\) ( 2 góc đối đỉnh).
Cho hai đường thẳng a, b song song với nhau, đường thẳng c vuông góc với a tại A và cắt b tại B. Hãy giải thích tại sao đường thẳng c cũng vuông góc với b.
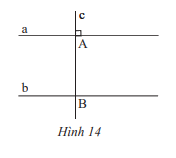
Phương pháp giải:
Sử dụng tính chất của 2 đường thẳng song song: Một đường thẳng cắt hai đường thẳng song song thì 2 góc đồng vị bằng nhau.
Lời giải chi tiết:
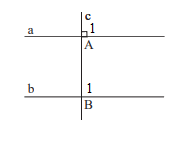
Vì a // b nên \(\widehat {{B_1}} = \widehat {{A_1}}\) (2 góc đồng vị), mà \(\widehat {{A_1}} = 90^\circ \) nên \(\widehat {{B_1}} = 90^\circ \).
Vậy c vuông góc với b.
Mục 3 trong SGK Toán 7 tập 1 chương trình Chân trời sáng tạo tập trung vào việc vận dụng các kiến thức đã học về số hữu tỉ, phép cộng, trừ, nhân, chia số hữu tỉ để giải quyết các bài toán thực tế và bài tập nâng cao. Các bài tập trong mục này thường yêu cầu học sinh phải hiểu rõ các quy tắc, tính chất của các phép toán và biết cách áp dụng chúng một cách linh hoạt.
Bài tập mục 3 trang 79, 80 bao gồm các dạng bài tập sau:
Để giải bài tập này, học sinh cần nắm vững các quy tắc ưu tiên phép toán: thực hiện các phép tính trong ngoặc trước, sau đó thực hiện các phép nhân, chia, cộng, trừ theo thứ tự từ trái sang phải.
Ví dụ: Tính giá trị của biểu thức (1/2 + 1/3) * 4/5
Khi giải bài toán thực tế, học sinh cần đọc kỹ đề bài, xác định các dữ kiện đã cho và yêu cầu của bài toán. Sau đó, sử dụng các kiến thức đã học để xây dựng phương trình hoặc biểu thức toán học phù hợp và giải để tìm ra đáp án.
Ví dụ: Một cửa hàng bán một chiếc áo với giá gốc là 100.000 đồng. Cửa hàng giảm giá 10% cho chiếc áo đó. Hỏi giá bán chiếc áo sau khi giảm giá là bao nhiêu?
Giải:
Để giải bài tập này, học sinh cần sử dụng các kiến thức về số hữu tỉ, các phép toán và các tính chất của chúng để tìm ra số hữu tỉ thỏa mãn điều kiện cho trước.
Có nhiều cách để so sánh các số hữu tỉ, ví dụ như:
Khi giải bài tập, học sinh cần lưu ý những điều sau:
Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin giải quyết các bài tập mục 3 trang 79, 80 SGK Toán 7 tập 1 chương trình Chân trời sáng tạo. Chúc các em học tập tốt!